Hard-core predicate
Encyclopedia
In cryptography
, a hard-core predicate of a one-way function
f is a predicate b (i.e., a function whose output is a single bit) which is easy to compute given x but is hard to compute given f(x). In formal terms, there is no probabilistic polynomial time algorithm that computes b(x) from f(x) with probability significantly greater than one half over random choice of x.
A hard-core function can be defined similarly.
A hard-core predicate captures "in a concentrated sense" the hardness of inverting f.
While a one-way function is hard to invert, there are no guarantees about the feasibility of computing partial information about the preimage c from the image f(x). For instance, while RSA is conjectured to be a one-way function, the Jacobi symbol
of the preimage can be easily computed from that of the image.
It is clear that if a one-to-one function
has a hard-core predicate, then it must be one way. Oded Goldreich
and Leonid Levin
(1989) showed how every one-way function can be trivially modified to obtain a one-way function that has a specific hard-core predicate. Let f be a one-way function. Define
where the length of r is the same as that of x. Let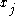
denote the jth bit of x and 
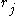the jth bit of r. Then
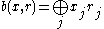
is a hard core predicate of g. Note that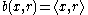
where 
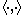denotes the standard inner product
on the vector space
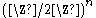. This predicate is hard-core due to computational issues; that is, it is not hard to compute because g(x, r) is information theoretically
lossy. Rather, if an algorithm exists to compute this predicate efficiently, then an algorithm exists to invert f efficiently. A similar construction yields a hard-core function with log (|x|) output bits.
It is sometimes the case that an actual bit of the input x is hard-core. For example, every single bit of inputs to the RSA function is a hard-core predicate of RSA and blocks of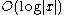
bits of x are indistinguishable from random bit strings in polynomial time (under the assumption that the RSA function is hard to invert).
Hard-core predicates give a way to construct a pseudorandom generator from any one-way permutation. If b is a hard-core predicate of a one way function f, and s is a random seed, then
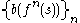
is a pseudorandom bit sequence.
Hard-core predicates of trapdoor one-way permutations (known as trapdoor predicates) can be used to construct semantically secure
public-key encryption schemes.
).
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, a hard-core predicate of a one-way function
One-way function
In computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here "easy" and "hard" are to be understood in the sense of computational complexity theory, specifically the theory of polynomial time problems...
f is a predicate b (i.e., a function whose output is a single bit) which is easy to compute given x but is hard to compute given f(x). In formal terms, there is no probabilistic polynomial time algorithm that computes b(x) from f(x) with probability significantly greater than one half over random choice of x.
A hard-core function can be defined similarly.
A hard-core predicate captures "in a concentrated sense" the hardness of inverting f.
While a one-way function is hard to invert, there are no guarantees about the feasibility of computing partial information about the preimage c from the image f(x). For instance, while RSA is conjectured to be a one-way function, the Jacobi symbol
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
of the preimage can be easily computed from that of the image.
It is clear that if a one-to-one function
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
has a hard-core predicate, then it must be one way. Oded Goldreich
Oded Goldreich
Oded Goldreich is a professor of Computer Science at the Faculty of Mathematics and Computer Science of Weizmann Institute of Science, Israel. His research interests lie within the theory of computation...
and Leonid Levin
Leonid Levin
-External links:* at Boston University....
(1989) showed how every one-way function can be trivially modified to obtain a one-way function that has a specific hard-core predicate. Let f be a one-way function. Define
- g(x, r) = (f(x), r),
where the length of r is the same as that of x. Let
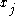denote the jth bit of x and 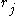the jth bit of r. Then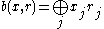is a hard core predicate of g. Note that
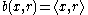where 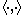denotes the standard inner productInner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
on the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
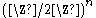. This predicate is hard-core due to computational issues; that is, it is not hard to compute because g(x, r) is information theoreticallyInformation theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
lossy. Rather, if an algorithm exists to compute this predicate efficiently, then an algorithm exists to invert f efficiently. A similar construction yields a hard-core function with log (|x|) output bits.
It is sometimes the case that an actual bit of the input x is hard-core. For example, every single bit of inputs to the RSA function is a hard-core predicate of RSA and blocks of
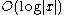bits of x are indistinguishable from random bit strings in polynomial time (under the assumption that the RSA function is hard to invert).Hard-core predicates give a way to construct a pseudorandom generator from any one-way permutation. If b is a hard-core predicate of a one way function f, and s is a random seed, then
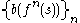
is a pseudorandom bit sequence.
Hard-core predicates of trapdoor one-way permutations (known as trapdoor predicates) can be used to construct semantically secure
Semantic security
Semantic security is a widely used definition for security in an asymmetric key encryption algorithm. For a cryptosystem to be semantically secure, it must be infeasible for a computationally bounded adversary to derive significant information about a message when given only its ciphertext and...
public-key encryption schemes.
See also
List-decoding (describes list decoding; the core of the Goldreich-Levin construction of hard-core predicates from one-way functions can be viewed as an algorithm for list-decoding the Hadamard codeHadamard code
The Hadamard code is an error-correcting code that is used for error detection and correction when transmitting messages over very noisy or unreliable channels....
).