
Hardy-Weinberg principle
Encyclopedia

Allele frequency
Allele frequency or Gene frequency is the proportion of all copies of a gene that is made up of a particular gene variant . In other words, it is the number of copies of a particular allele divided by the number of copies of all alleles at the genetic place in a population. It can be expressed for...
and genotype
Genotype frequency
In population genetics, the genotype frequency is the frequency or proportion In population genetics, the genotype frequency is the frequency or proportion In population genetics, the genotype frequency is the frequency or proportion (i.e. 0 In population genetics, the genotype frequency is the...
frequencies in a population remain constant—that is, they are in equilibrium—from generation to generation unless specific disturbing influences are introduced. Those disturbing influences include non-random mating
Mating
In biology, mating is the pairing of opposite-sex or hermaphroditic organisms for copulation. In social animals, it also includes the raising of their offspring. Copulation is the union of the sex organs of two sexually reproducing animals for insemination and subsequent internal fertilization...
, mutation
Mutation
In molecular biology and genetics, mutations are changes in a genomic sequence: the DNA sequence of a cell's genome or the DNA or RNA sequence of a virus. They can be defined as sudden and spontaneous changes in the cell. Mutations are caused by radiation, viruses, transposons and mutagenic...
s, selection
Selection
In the context of evolution, certain traits or alleles of genes segregating within a population may be subject to selection. Under selection, individuals with advantageous or "adaptive" traits tend to be more successful than their peers reproductively—meaning they contribute more offspring to the...
, limited population
Population
A population is all the organisms that both belong to the same group or species and live in the same geographical area. The area that is used to define a sexual population is such that inter-breeding is possible between any pair within the area and more probable than cross-breeding with individuals...
size, "overlapping generations", random genetic drift, gene flow
Gene flow
In population genetics, gene flow is the transfer of alleles of genes from one population to another.Migration into or out of a population may be responsible for a marked change in allele frequencies...
and meiotic drive. It is important to understand that outside the lab, one or more of these "disturbing influences" are always in effect. That is, Hardy–Weinberg equilibrium is impossible in nature. Genetic equilibrium is an ideal state that provides a baseline against which to measure change.
Static allele frequencies in a population across generations assume: no mutation (the alleles don't change), no migration or emigration (no exchange of alleles between populations), infinitely large population size, and no selective pressure for or against any genotypes. Genotype frequencies will also be static when mating is random.
In the simplest case of a single locus with two allele
Allele
An allele is one of two or more forms of a gene or a genetic locus . "Allel" is an abbreviation of allelomorph. Sometimes, different alleles can result in different observable phenotypic traits, such as different pigmentation...
s: the dominant allele is denoted A and the recessive a and their frequencies are denoted by p and q; freq(A) = p; freq(a) = q; p + q = 1. If the population is in equilibrium, then we will have freq(AA) = p2 for the AA homozygotes in the population, freq(aa) = q2 for the aa homozygotes, and freq(Aa) = 2pq for the heterozygotes.
This concept was named after G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and Wilhelm Weinberg
Wilhelm Weinberg
Dr Wilhelm Weinberg was a German half-Jewish physician and obstetrician-gynecologist, practicing in Stuttgart, who in a 1908 paper Dr Wilhelm Weinberg (Stuttgart, December 25, 1862 – Tübingen, November 27, 1937) was a German half-Jewish physician and obstetrician-gynecologist, practicing in...
.
Derivation
A better, but equivalent, probabilisticProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
description for the HWP is that the alleles for the next generation for any given individual are chosen randomly and independent of each other. Consider two alleles, A and a, with frequencies p and q, respectively, in the population. The different ways to form new genotypes can be derived using a Punnett square
Punnett square
The Punnett square is a diagram that is used to predict an outcome of a particular cross or breeding experiment. It is named after Reginald C. Punnett, who devised the approach, and is used by biologists to determine the probability of an offspring's having a particular genotype...
, where the fraction in each is equal to the product of the row and column probabilities.
| Females | |||
|---|---|---|---|
| A (p) | a (q) | ||
| Males | A (p) | AA (p2) | Aa (pq) |
| a (q) | Aa (pq) | aa (q2) | |
The formula is sometimes written as (p2) + (2pq) + (q2) = 1, representing the fact that probabilities (normalised frequencies for a theoretically infinite population size) must add up to one.
The final three possible genotypic frequencies in the offspring become:
These frequencies are called Hardy–Weinberg frequencies (or Hardy–Weinberg proportions). This is achieved in one generation, and only requires the assumption of random mating with an infinite population size.
Sometimes, a population is created by bringing together males and females with different allele frequencies. In this case, the assumption of a single population is violated until after the first generation, so the first generation will not have Hardy–Weinberg equilibrium. Successive generations will have Hardy–Weinberg equilibrium.
Deviations from Hardy–Weinberg equilibrium
Violations of the Hardy–Weinberg assumptions can cause deviations from expectationExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
. How this affects the population depends on the assumptions that are violated.
- Random mating. The HWP states the population will have the given genotypic frequencies (called Hardy–Weinberg proportions) after a single generation of random mating within the population. When violations of this provision occur, the population will not have Hardy–Weinberg proportions. Three such violations are:
- InbreedingInbreedingInbreeding is the reproduction from the mating of two genetically related parents. Inbreeding results in increased homozygosity, which can increase the chances of offspring being affected by recessive or deleterious traits. This generally leads to a decreased fitness of a population, which is...
, which causes an increase in homozygosityZygosityZygosity refers to the similarity of alleles for a trait in an organism. If both alleles are the same, the organism is homozygous for the trait. If both alleles are different, the organism is heterozygous for that trait...
for all genes. - Assortative matingAssortative matingAssortative mating , and the related concept Disassortative mating, is the phenomenon where a sexually reproducing organism chooses to mate with individuals that are similar or dissimilar to itself in some specific manner...
, which causes an increase in homozygosityZygosityZygosity refers to the similarity of alleles for a trait in an organism. If both alleles are the same, the organism is homozygous for the trait. If both alleles are different, the organism is heterozygous for that trait...
only for those genes involved in the trait that is assortatively mated (and genes in linkage disequilibriumLinkage disequilibriumIn population genetics, linkage disequilibrium is the non-random association of alleles at two or more loci, not necessarily on the same chromosome. It is also referred to as to as gametic phase disequilibrium , or simply gametic disequilibrium...
with them). This form of deviation from the Hardy–Weinberg equilibrium denotes the evolution of a species.
- Inbreeding
If a population violates one of the following four assumptions, the population may continue to have Hardy–Weinberg proportions each generation, but the allele frequencies will change with that force.
- SelectionNatural selectionNatural selection is the nonrandom process by which biologic traits become either more or less common in a population as a function of differential reproduction of their bearers. It is a key mechanism of evolution....
, in general, causes allele frequencies to change, often quite rapidly. While directional selectionDirectional selectionIn population genetics, directional selection is a mode of natural selection in which a single phenotype is favored, causing the allele frequency to continuously shift in one direction...
eventually leads to the loss of all alleles except the favored one, some forms of selection, such as balancing selectionBalancing selectionBalancing selection refers to a number of selective processes by which multiple alleles are actively maintained in the gene pool of a population at frequencies above that of gene mutation. This usually happens when the heterozygotes for the alleles under consideration have a higher adaptive value...
, lead to equilibrium without loss of alleles. - MutationMutationIn molecular biology and genetics, mutations are changes in a genomic sequence: the DNA sequence of a cell's genome or the DNA or RNA sequence of a virus. They can be defined as sudden and spontaneous changes in the cell. Mutations are caused by radiation, viruses, transposons and mutagenic...
will have a very subtle effect on allele frequencies. Mutation rates are of the order 10−4 to 10−8, and the change in allele frequency will be, at most, the same order. Recurrent mutation will maintain alleles in the population, even if there is strong selection against them. - Migration genetically links two or more populations together. In general, allele frequencies will become more homogeneous among the populations. Some models for migration inherently include nonrandom mating (Wahlund effectWahlund effectIn population genetics, the Wahlund effect refers to reduction of heterozygosity in a population caused by subpopulation structure. Namely, if two or more subpopulations have different allele frequencies then the overall heterozygosity is reduced, even if the subpopulations themselves are in a...
, for example). For those models, the Hardy–Weinberg proportions will normally not be valid. - Small population sizeSmall population sizeSmall populations behave differently from larger populations. They often result in population bottlenecks, which have harmful consequences for the survival of that population.-Demographic effects:...
can cause a random change in allele frequencies. This is due to a sampling effect, and is called genetic driftGenetic driftGenetic drift or allelic drift is the change in the frequency of a gene variant in a population due to random sampling.The alleles in the offspring are a sample of those in the parents, and chance has a role in determining whether a given individual survives and reproduces...
. Sampling effects are most important when population sizes are small or the allele is rare.
How these violations affect formal statistical tests for HWE is discussed later.
Unfortunately, violations of assumptions in the Hardy–Weinberg principle does not mean the population will violate HWE. For example, balancing selection leads to an equilibrium population with Hardy–Weinberg proportions. This property with selection vs. mutation is the basis for many estimates of mutation rate (call mutation-selection balance
Mutation-selection balance
The mutation-selection balance is a classic result in population geneticsfirst derived in the 1920s by John Burdon Sanderson Haldane and R.A. Fisher.A genetic variant that is deleterious will not necessarily disappear immediately from apopulation...
).
Sex linkage
Where the A gene is sex linkedSex linkage
Sex linkage is the phenotypic expression of an allele related to the chromosomal sex of the individual. This mode of inheritance is in contrast to the inheritance of traits on autosomal chromosomes, where both sexes have the same probability of inheritance...
, the heterogametic sex (e.g., mammalian males; avian females) have only one copy of the gene (and are termed hemizygous), while the homogametic sex (e.g., human
Human
Humans are the only living species in the Homo genus...
females) have two copies. The genotype frequencies at equilibrium are p and q for the heterogametic sex but p2, 2pq and q2 for the homogametic sex.
For example, in humans red–green colorblindness is an X-linked recessive trait. In western European males, the trait affects about 1 in 12, (q = 0.083) whereas it affects about 1 in 200 females (0.005, compared to q2 = 0.007), very close to Hardy–Weinberg proportions.
If a population is brought together with males and females with different allele frequencies, the allele frequency of the male population follows that of the female population because each receives its X chromosome from its mother. The population converges on equilibrium very quickly.
Generalizations
The simple derivation above can be generalized for more than two alleles and polyploidyPolyploidy
Polyploid is a term used to describe cells and organisms containing more than two paired sets of chromosomes. Most eukaryotic species are diploid, meaning they have two sets of chromosomes — one set inherited from each parent. However polyploidy is found in some organisms and is especially common...
.
Generalization for more than two alleles
Consider an extra allele frequency, r. The two-allele case is the binomial expansionBinomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
of (p + q)2, and thus the three-allele case is the trinomial expansion of (p + q+ r)2.
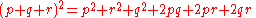
More generally, consider the alleles A1, ..., Ai given by the allele frequencies p1 to pi;

giving for all homozygotes
Zygosity
Zygosity refers to the similarity of alleles for a trait in an organism. If both alleles are the same, the organism is homozygous for the trait. If both alleles are different, the organism is heterozygous for that trait...
:
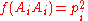
and for all heterozygotes
Zygosity
Zygosity refers to the similarity of alleles for a trait in an organism. If both alleles are the same, the organism is homozygous for the trait. If both alleles are different, the organism is heterozygous for that trait...
:
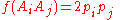
Generalization for polyploidy
The Hardy–Weinberg principle may also be generalized to polyploid systems, that is, for organisms that have more than two copies of each chromosome. Consider again only two alleles. The diploid case is the binomial expansionBinomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
of:

and therefore the polyploid case is the polynomial expansion
Polynomial expansion
In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition...
of:

where c is the ploidy
Ploidy
Ploidy is the number of sets of chromosomes in a biological cell.Human sex cells have one complete set of chromosomes from the male or female parent. Sex cells, also called gametes, combine to produce somatic cells. Somatic cells, therefore, have twice as many chromosomes. The haploid number is...
, for example with tetraploid (c = 4):
| Genotype | Frequency |
|---|---|
 |
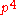 |
 |
 |
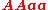 |
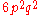 |
 |
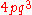 |
 |
 |
Depending on whether the organism is a 'true' tetraploid or an amphidiploid will determine how long it will take for the population to reach Hardy–Weinberg equilibrium.
Complete generalization
For distinct alleles in
distinct alleles in  -ploids, the genotype frequencies in the Hardy–Weinberg equilibrium are given by individual terms in the multinomial expansion
-ploids, the genotype frequencies in the Hardy–Weinberg equilibrium are given by individual terms in the multinomial expansionMultinomial theorem
In mathematics, the multinomial theorem says how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem to polynomials.-Theorem:...
of
 :
: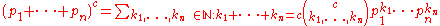
Applications
The Hardy–Weinberg principle may be applied in two ways, either a population is assumed to be in Hardy–Weinberg proportions, in which the genotype frequencies can be calculated, or if the genotype frequencies of all three genotypes are known, they can be tested for deviations that are statistically significant.Application to cases of complete dominance
Suppose that the phenotypes of AA and Aa are indistinguishable, i.e., there is complete dominanceDominance relationship
Dominance in genetics is a relationship between two variant forms of a single gene, in which one allele masks the effect of the other in influencing some trait. In the simplest case, if a gene exists in two allelic forms , three combinations of alleles are possible: AA, AB, and BB...
. Assuming that the Hardy–Weinberg principle applies to the population, then
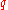 can still be calculated from f(aa):
can still be calculated from f(aa):
and
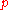 can be calculated from
can be calculated from  . And thus an estimate of f(AA) and f(Aa) derived from
. And thus an estimate of f(AA) and f(Aa) derived from 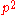 and
and  respectively. Note however, such a population cannot be tested for equilibrium using the significance tests below because it is assumed a priori
respectively. Note however, such a population cannot be tested for equilibrium using the significance tests below because it is assumed a prioriA priori and a posteriori (philosophy)
The terms a priori and a posteriori are used in philosophy to distinguish two types of knowledge, justifications or arguments...
.
Significance tests for deviation
Testing deviation from the HWP is generally performed using Pearson'sKarl Pearson
Karl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....
chi-squared test
Pearson's chi-squared test
Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
, using the observed genotype frequencies obtained from the data and the expected genotype frequencies obtained using the HWP. For systems where there are large numbers of alleles, this may result in data with many empty possible genotypes and low genotype counts, because there are often not enough individuals present in the sample to adequately represent all genotype classes. If this is the case, then the asymptotic assumption of the chi-squared distribution, will no longer hold, and it may be necessary to use a form of Fisher's
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
exact test
Fisher's exact test
Fisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
, which requires a computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
to solve. More recently a number of MCMC
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
methods of testing for deviations from HWP have been proposed (Guo & Thompson, 1992; Wigginton et al. 2005)
Example χ2 test for deviation
These data are from E.B. FordE.B. Ford
Edmund Brisco "Henry" Ford FRS Hon. FRCP was a British ecological geneticist. He was a leader among those British biologists who investigated the role of natural selection in nature. As a schoolboy Ford became interested in lepidoptera, the group of insects which includes butterflies and moths...
(1971) on the Scarlet tiger moth
Scarlet tiger moth
The Scarlet Tiger Moth is a colorful moth of Europe, Turkey, Transcaucasus, northern Iran. It belongs to the tiger moth family, Arctiidae....
, for which the phenotype
Phenotype
A phenotype is an organism's observable characteristics or traits: such as its morphology, development, biochemical or physiological properties, behavior, and products of behavior...
s of a sample of the population were recorded. Genotype-phenotype distinction
Genotype-phenotype distinction
The genotype–phenotype distinction is drawn in genetics. "Genotype" is an organism's full hereditary information, even if not expressed. "Phenotype" is an organism's actual observed properties, such as morphology, development, or behavior...
is assumed to be negligibly small. The null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
is that the population is in Hardy–Weinberg proportions, and the alternative hypothesis is that the population is not in Hardy–Weinberg proportions.
| Phenotype | White-spotted (AA) | Intermediate (Aa) | Little spotting (aa) | Total |
|---|---|---|---|---|
| Number | 1469 | 138 | 5 | 1612 |
From which allele frequencies can be calculated:
-

and
-

So the Hardy–Weinberg expectationExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
is:
-

Pearson's chi-squared testPearson's chi-squared testPearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
states:
-

There is 1 degree of freedomDegrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
(degrees of freedom for test for Hardy–Weinberg proportions are # genotypes − # alleles). The 5% significance level for 1 degree of freedom is 3.84, and since the χ2 value is less than this, the null hypothesisNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
that the population is in Hardy–Weinberg frequencies is not rejected.
Fisher's exact test (probability test)
Fisher's exact testFisher's exact testFisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
can be applied to testing for Hardy–Weinberg proportions. Because the test is conditional on the allele frequencies, p and q, the problem can be viewed as testing for the proper number of heterozygotes. In this way, the hypothesis of Hardy–Weinberg proportions is rejected if the number of heterozygotes are too large or too small. The conditional probabilities for the heterozygote, given the allele frequencies are given in Emigh (1980) as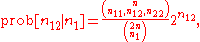
where n11, n12, n22 are the observed numbers of the three genotypes, AA, Aa, and aa, respectively, and n1 is the number of A alleles, where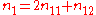 .
.
An example
Using one of the examples from Emigh (1980), we can consider the case where n = 100, and p = 0.34. The possible observed heterozygotes and their exact significance level is given in Table 4.Table 4: Example of Fisher's Exact Test for n = 100, p = 0.34. Number of heterozygotes Significance level 0 0.000 2 0.000 4 0.000 6 0.000 8 0.000 10 0.000 12 0.000 14 0.000 16 0.000 18 0.001 20 0.007 22 0.034 24 0.067 26 0.151 28 0.291 30 0.474 32 0.730 34 1.000
Using this table, you look up the significance level of the test based on the observed number of heterozygotes. For example, if you observed 20 heterozygotes, the significance level for the test is 0.007. As is typical for Fisher's exact test for small samples, the gradation of significance levels is quite coarse.
Unfortunately, you have to create a table like this for every experiment, since the tables are dependent on both n and p.
Inbreeding coefficient
The inbreeding coefficient, F (see also F-statisticsF-statisticsIn population genetics, F-statistics describe the level of heterozygosity in a population; more specifically the degree of a reduction in heterozygosity when compared to Hardy–Weinberg expectation...
), is one minus the observed frequency of heterozygotes over that expected from Hardy–Weinberg equilibrium.
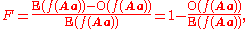
where the expected value from Hardy–Weinberg equilibrium is given by

For example, for Ford's data above;

For two alleles, the chi-squared goodness of fit test for Hardy–Weinberg proportions is equivalent to the test for inbreeding, F = 0.
The inbreeding coefficient is unstable as the expected value approaches zero, and thus not useful for rare and very common alleles. For: E = 0, O > 0, F = −∞ and E = 0, O = 0, F is undefined.
History
Mendelian genetics were rediscovered in 1900. However, it remained somewhat controversial for several years as it was not then known how it could cause continuous characteristics. Udny YuleUdny YuleGeorge Udny Yule FRS , usually known as Udny Yule, was a British statistician, born at Beech Hill, a house in Morham near Haddington, Scotland and died in Cambridge, England. His father, also George Udny Yule, and a nephew, were knighted. His uncle was the noted orientalist Sir Henry Yule...
(1902) argued against Mendelism because he thought that dominant alleles would increase in the population. The AmericanUnited StatesThe United States of America is a federal constitutional republic comprising fifty states and a federal district...
William E. CastleWilliam E. CastleWilliam Ernest Castle was an early American geneticist.-Early years:William Ernest Castle was born on a farm in Ohio and took an early interest in natural history...
(1903) showed that without selectionSelectionIn the context of evolution, certain traits or alleles of genes segregating within a population may be subject to selection. Under selection, individuals with advantageous or "adaptive" traits tend to be more successful than their peers reproductively—meaning they contribute more offspring to the...
, the genotype frequencies would remain stable. Karl PearsonKarl PearsonKarl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....
(1903) found one equilibrium position with values of p = q = 0.5. Reginald PunnettReginald PunnettProfessor Reginald Crundall Punnett FRS was a British geneticist who co-founded, with William Bateson, the Journal of Genetics in 1910. Punnett is probably best remembered today as the creator of the Punnett square, a tool still used by biologists to predict the probability of possible genotypes...
, unable to counter Yule's point, introduced the problem to G. H. Hardy, a BritishUnited KingdomThe United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
mathematicianMathematicianA mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, with whom he played cricketCricketCricket is a bat-and-ball game played between two teams of 11 players on an oval-shaped field, at the centre of which is a rectangular 22-yard long pitch. One team bats, trying to score as many runs as possible while the other team bowls and fields, trying to dismiss the batsmen and thus limit the...
. Hardy was a pure mathematicianPure mathematicsBroadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
and held applied mathematicsApplied mathematicsApplied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
in some contempt; his view of biologists' use of mathematics comes across in his 1908 paper where he describes this as "very simple".
- To the Editor of Science: I am reluctant to intrude in a discussion concerning matters of which I have no expert knowledge, and I should have expected the very simple point which I wish to make to have been familiar to biologists. However, some remarks of Mr. Udny Yule, to which Mr. R. C. Punnett has called my attention, suggest that it may still be worth making...
- Suppose that Aa is a pair of Mendelian characters, A being dominant, and that in any given generation the number of pure dominants (AA), heterozygotes (Aa), and pure recessives (aa) are as p:2q:r. Finally, suppose that the numbers are fairly large, so that mating may be regarded as random, that the sexes are evenly distributed among the three varieties, and that all are equally fertile. A little mathematics of the multiplication-table type is enough to show that in the next generation the numbers will be as (p+q)2:2(p+q)(q+r):(q+r)2, or as p1:2q1:r1, say.
- The interesting question is — in what circumstances will this distribution be the same as that in the generation before? It is easy to see that the condition for this is q2 = pr. And since q12 = p1r1, whatever the values of p, q, and r may be, the distribution will in any case continue unchanged after the second generation
The principle was thus known as Hardy's law in the English-speaking worldAnglosphereAnglosphere is a neologism which refers to those nations with English as the most common language. The term can be used more specifically to refer to those nations which share certain characteristics within their cultures based on a linguistic heritage, through being former British colonies...
until 1943, when Curt Stern pointed out that it had first been formulated independently in 1908 by the German physician Wilhelm WeinbergWilhelm WeinbergDr Wilhelm Weinberg was a German half-Jewish physician and obstetrician-gynecologist, practicing in Stuttgart, who in a 1908 paper Dr Wilhelm Weinberg (Stuttgart, December 25, 1862 – Tübingen, November 27, 1937) was a German half-Jewish physician and obstetrician-gynecologist, practicing in...
. Others have attempted to associate Castle'sWilliam E. CastleWilliam Ernest Castle was an early American geneticist.-Early years:William Ernest Castle was born on a farm in Ohio and took an early interest in natural history...
name with the Law because of his work in 1903, but it is only rarely seen as the Hardy–Weinberg–Castle Law.
Derivation of Hardy’s equations
The derivation of Hardy’s equations is illustrative. He begins with a population of genotypes consisting of pure dominants (AA), heterozygotes (Aa), and pure recessives (aa) in the relative proportions p:2q:r with the conditions noted above, that is,
-

Rewriting this as (p + q) + (q + r) = 1 and squaring both sides yields Hardy’s result:
-

Hardy’s equivalence condition is
-
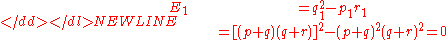
for generations after the first. For a putative third generation,
-
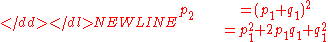
Substituting for p1 and q1 and factoring out (p + q)2 yields,
-
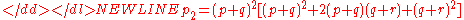
The quantity in brackets is equal to 1, therefore, p2 = p1 and will remain so for succeeding generations. The result will be the same for the other two genotypes.
Numerical example
An example computation of the genotype distribution given by Hardy's original equations is instructive. The phenotype distribution from Table 3 above will be used to compute Hardy's initial genotype distribution. Note that the p and q values used by Hardy are not the same as those used above.
-

-
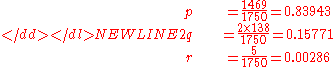
As checks on the distribution, compute-
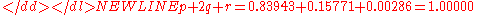
and
-

For the next generation, Hardy's equations give,-
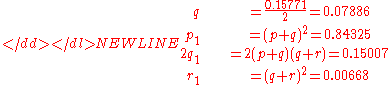
Again as checks on the distribution, compute
-

and
-

which are the expected values. The reader may demonstrate that subsequent use of the second-generation values for a third generation will yield identical results.
Graphical representation
It is possible to represent the distribution of genotype frequencies for a bi-allelic locus within a population graphically using a de Finetti diagramDe Finetti diagramA de Finetti diagram is a ternary plot used in population genetics. It is named after the Italian statistician Bruno de Finetti and is used to graph the genotype frequencies of populations, where there are two alleles and the population is diploid...
. This uses a triangular plot (also known as trilinear, triaxial or ternary plotTernary plotA ternary plot, ternary graph, triangle plot, simplex plot, or de Finetti diagram is a barycentric plot on three variables which sum to a constant. It graphically depicts the ratios of the three variables as positions in an equilateral triangle...
) to represent the distribution of the three genotype frequencies in relation to each other. Although it differs from many other such plots in that the direction of one of the axes has been reversed.
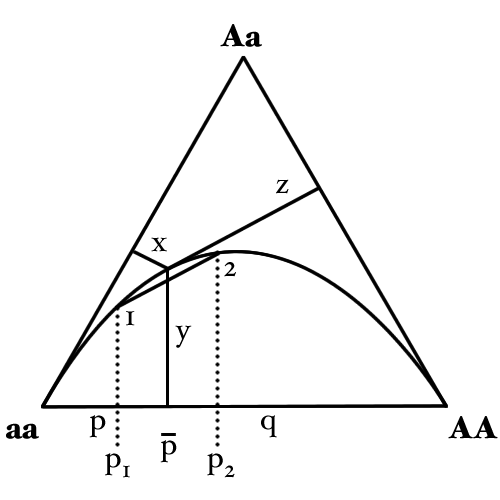
The curved line in the above diagram is the Hardy–Weinberg parabola and represents the state where alleles are in Hardy–Weinberg equilibrium.
It is possible to represent the effects of Natural SelectionNatural selectionNatural selection is the nonrandom process by which biologic traits become either more or less common in a population as a function of differential reproduction of their bearers. It is a key mechanism of evolution....
and its effect on allele frequency on such graphs (e.g. Ineichen & Batschelet 1975)
The de Finetti diagramDe Finetti diagramA de Finetti diagram is a ternary plot used in population genetics. It is named after the Italian statistician Bruno de Finetti and is used to graph the genotype frequencies of populations, where there are two alleles and the population is diploid...
has been developed and used extensively by A. W. F. EdwardsA. W. F. EdwardsAnthony William Fairbank Edwards is a British statistician, geneticist, and evolutionary biologist, sometimes called Fisher's Edwards. He is a Life Fellow of Gonville and Caius College and retired Professor of Biometry at the University of Cambridge, and holds both the ScD and LittD degrees. A...
in his book Foundations of Mathematical Genetics.
External links
- EvolutionSolution (at bottom of page)
- Hardy–Weinberg Equilibrium Calculator
- Population Genetics Simulator
- HARDY C implementation of Guo & Thompson 1992
- Source code (C/C++/Fortran/R) for Wigginton et al. 2005
- Online de Finetti Diagram Generator and Hardy–Weinberg equilibrium tests
- Online Hardy–Weinberg equilibrium tests and drawing of de Finetti diagrams
- Hardy–Weinberg Equilibrium Calculator
-
-
-
-
-
-
-
-
-
-
-
-
-
-




