Harmonic superspace
Encyclopedia
In supersymmetry
, harmonic superspace
is one way of dealing with supersymmetric theories with 8 real SUSY generators in a manifestly covariant manner. It turns out that the 8 real SUSY generators are pseudoreal, and after complexification
, correspond to the tensor product
of a four dimensional Dirac spinor with the fundamental representation
of SU(2)R. The quotient space
, which is a 2-sphere/Riemann sphere
.
Harmonic superspace describes N=2 D=4, N=1 D=5, and N=(1,0) D=6 SUSY in a manifestly covariant manner.
There are many possible coordinate systems over S2, but the one chosen not only involves redundant coordinates, but also happen to be a coordinatization of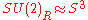
. We only get S2 after a projection over 
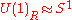. This is of course the Hopf fibration. Consider the left action of SU(2)R upon itself. We can then extend this to the space of complex valued smooth functions over SU(2)R. In particular, we have the subspace of functions which transform as the fundamental representation under SU(2)R. The fundamental representation (up to isomorphism, of course) is a two dimensional complex vector space. Let us denote the indices of this representation by i,j,k,...=1,2. The subspace of interest consists of two copies of the fundamental representation. Under the right action by U(1)R -- which commutes with any left action—one copy has a "charge" of +1, and the other of -1. Let us label the basis functions 
.
.
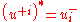The redundancy in the coordinates is given by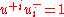
.
Everything can be interpreted in terms of algebraic geometry
. The projection is given by the "gauge transformation"
where φ is any real number. Think of S3 as a U(1)R-principal bundle
over S2 with a nonzero first Chern class
. Then, "fields" over S2 are characterized by an integral U(1)R charge given by the right action of U(1)R. For instance, u+ has a charge of +1, and u- of -1. By convention, fields with a charge of +r are denoted by a superscript with r +'s, and ditto for fields with a charge of -r. R-charges are additive under the multiplication of fields.
The SUSY charges are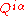
, and the corresponding fermionic coordinates are 
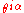. Harmonic superspace is given by the product of ordinary extended superspace (with 8 real fermionic coordinatates) with S2 with the nontrivial U(1)R bundle over it. The product is somewhat twisted in that the fermionic coordinates are also charged under U(1)R. This charge is given by
.
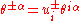We can define the covariant derivative
s
with the property that they supercommute with the SUSY transformations, and 
where f is any function of the harmonic variables. Similarly, define
and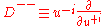
.
A chiral superfield q with an R-charge of r satisfies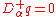
. A scalar hypermultiplet is given by a chiral superfield 
. We have the additional constraint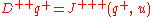
.
According to the Atiyah-Singer index theorem, the solution space to the previous constraint is a two dimensional complex manifold.
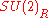can be identified with the Lie group of quaternion
s with unit norm under multiplication.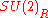
, and hence the quaternions act upon the tangent space of extended superspace. The bosonic spacetime dimensions transform trivially under 
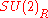while the fermionic dimensions transform according to the fundamental representation
. The left multiplication by quaternions is linear. Now consider the subspace of unit quaternions with no real component, which is isomorphic to S2. Each element of this subspace can act as the imaginary number i in a complex subalgebra of the quaternions. So, for each element of S2, we can use the corresponding imaginary unit to define a complex-real
structure over the extended superspace with 8 real SUSY generators. The totality of all CR structures for each point in S2 is harmonic superspace.
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
, harmonic superspace
is one way of dealing with supersymmetric theories with 8 real SUSY generators in a manifestly covariant manner. It turns out that the 8 real SUSY generators are pseudoreal, and after complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
, correspond to the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of a four dimensional Dirac spinor with the fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
of SU(2)R. The quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
, which is a 2-sphere/Riemann sphereRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
.
Harmonic superspace describes N=2 D=4, N=1 D=5, and N=(1,0) D=6 SUSY in a manifestly covariant manner.
There are many possible coordinate systems over S2, but the one chosen not only involves redundant coordinates, but also happen to be a coordinatization of
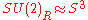. We only get S2 after a projection over 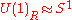. This is of course the Hopf fibration. Consider the left action of SU(2)R upon itself. We can then extend this to the space of complex valued smooth functions over SU(2)R. In particular, we have the subspace of functions which transform as the fundamental representation under SU(2)R. The fundamental representation (up to isomorphism, of course) is a two dimensional complex vector space. Let us denote the indices of this representation by i,j,k,...=1,2. The subspace of interest consists of two copies of the fundamental representation. Under the right action by U(1)R -- which commutes with any left action—one copy has a "charge" of +1, and the other of -1. Let us label the basis functions ..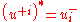The redundancy in the coordinates is given by
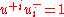.Everything can be interpreted in terms of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. The projection is given by the "gauge transformation"
where φ is any real number. Think of S3 as a U(1)R-principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over S2 with a nonzero first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
. Then, "fields" over S2 are characterized by an integral U(1)R charge given by the right action of U(1)R. For instance, u+ has a charge of +1, and u- of -1. By convention, fields with a charge of +r are denoted by a superscript with r +'s, and ditto for fields with a charge of -r. R-charges are additive under the multiplication of fields.
The SUSY charges are
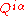, and the corresponding fermionic coordinates are 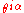. Harmonic superspace is given by the product of ordinary extended superspace (with 8 real fermionic coordinatates) with S2 with the nontrivial U(1)R bundle over it. The product is somewhat twisted in that the fermionic coordinates are also charged under U(1)R. This charge is given by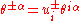.We can define the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s
with the property that they supercommute with the SUSY transformations, and where f is any function of the harmonic variables. Similarly, defineand
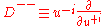.A chiral superfield q with an R-charge of r satisfies
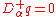. A scalar hypermultiplet is given by a chiral superfield . We have the additional constraint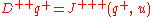.According to the Atiyah-Singer index theorem, the solution space to the previous constraint is a two dimensional complex manifold.
Relation to quaternions
The group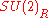 can be identified with the Lie group of quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s with unit norm under multiplication.
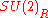, and hence the quaternions act upon the tangent space of extended superspace. The bosonic spacetime dimensions transform trivially under 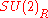while the fermionic dimensions transform according to the fundamental representationFundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
. The left multiplication by quaternions is linear. Now consider the subspace of unit quaternions with no real component, which is isomorphic to S2. Each element of this subspace can act as the imaginary number i in a complex subalgebra of the quaternions. So, for each element of S2, we can use the corresponding imaginary unit to define a complex-real
CR manifold
In mathematics, a CR manifold is a differentiable manifold together with a geometric structure modeled on that of a real hypersurface in a complex vector space, or more generally modeled on an edge of a wedge....
structure over the extended superspace with 8 real SUSY generators. The totality of all CR structures for each point in S2 is harmonic superspace.