
Harnack's curve theorem
Encyclopedia
In real
algebraic geometry
, Harnack's curve theorem, named after Axel Harnack
, describes the possible numbers of connected component
s that an algebraic curve can have, in terms of the degree of the curve. For any algebraic curve
of degree m in the real projective plane
, the number of components c is bounded by
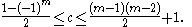
The maximum number is one more than the maximum genus
of a curve of degree m, attained when the curve is nonsingular. Moreover, any number of components in this range of possible values can be attained.
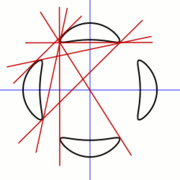 A curve which attains the maximum number of real components is called an
A curve which attains the maximum number of real components is called an
M-curve (from "maximum") – for example, an elliptic curve
with two components, such as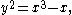 or the Trott curve
or the Trott curve
, a quartic with four components, are examples of M-curves.
This theorem formed the background to Hilbert's sixteenth problem
.
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, Harnack's curve theorem, named after Axel Harnack
Carl Gustav Axel Harnack
Carl Gustav Axel Harnack was a German mathematician who contributed to potential theory. Harnack's inequality applied to harmonic functions...
, describes the possible numbers of connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
s that an algebraic curve can have, in terms of the degree of the curve. For any algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of degree m in the real projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
, the number of components c is bounded by
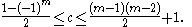
The maximum number is one more than the maximum genus
Geometric genus
In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
of a curve of degree m, attained when the curve is nonsingular. Moreover, any number of components in this range of possible values can be attained.

M-curve (from "maximum") – for example, an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
with two components, such as
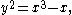 or the Trott curve
or the Trott curveTrott curve
In real algebraic geometry, a general quartic plane curve has 28 bitangent lines, lines that are tangent to the curve in two places. These lines exist in the complex projective plane, but it is possible to define curves for which all 28 of these lines have real numbers as their coordinates and...
, a quartic with four components, are examples of M-curves.
This theorem formed the background to Hilbert's sixteenth problem
Hilbert's sixteenth problem
Hilbert's 16th problem was posed by David Hilbert at the Paris conference of the International Congress of Mathematicians in 1900, together with the other 22 problems....
.

