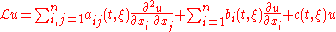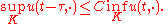Harnack's inequality
Encyclopedia
In mathematics, Harnack's inequality is an inequality relating the values of a positive harmonic function at two points, introduced by . and generalized Harnack's inequality to solutions of elliptic or parabolic partial differential equation
s. Perelman
's solution of the Poincaré conjecture
uses a version of the Harnack inequality, found by , for the Ricci flow
. Harnack's inequality is used to prove Harnack's theorem about the convergence of sequences of harmonic functions. Harnack's inequality also implies the regularity
of the function in the interior of its domain.
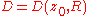 be an open
be an open
disk
in the plane and let f be a harmonic function
on D such that f(z) is non-negative for all . Then the following inequality holds for all
. Then the following inequality holds for all  :
:
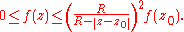
For general domains in
in  the inequality can be stated as follows: If
the inequality can be stated as follows: If  is a bounded domain with
is a bounded domain with  , then there is a constant
, then there is a constant  such that
such that

for every twice differentiable, harmonic and nonnegative function . The constant
. The constant  is independent of
is independent of  ; it depends only on the domain.
; it depends only on the domain.
of the data: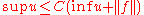
The constant depends on the ellipticity of the equation and the connected open region.
.
Let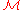 be a smooth domain in
be a smooth domain in 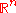 and consider the linear parabolic operator
and consider the linear parabolic operator
with smooth and bounded coefficients and a nondegenerate matrix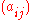 . Suppose that
. Suppose that  is a solution of
is a solution of
such that
Let be a compact subset of
be a compact subset of 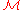 and choose
and choose 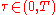 . Then for each
. Then for each  there exists a constant
there exists a constant  (depending only on
(depending only on  ,
,  and the coefficients of
and the coefficients of 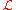 ) such that
) such that
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
's solution of the Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
uses a version of the Harnack inequality, found by , for the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
. Harnack's inequality is used to prove Harnack's theorem about the convergence of sequences of harmonic functions. Harnack's inequality also implies the regularity
Hölder condition
In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
of the function in the interior of its domain.
The statement
Let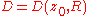 be an open
be an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
disk
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
in the plane and let f be a harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
on D such that f(z) is non-negative for all
 . Then the following inequality holds for all
. Then the following inequality holds for all  :
: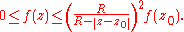
For general domains
 in
in  the inequality can be stated as follows: If
the inequality can be stated as follows: If  is a bounded domain with
is a bounded domain with  , then there is a constant
, then there is a constant  such that
such that
for every twice differentiable, harmonic and nonnegative function
 . The constant
. The constant  is independent of
is independent of  ; it depends only on the domain.
; it depends only on the domain.Elliptic partial differential equations
For elliptic partial differential equations, Harnack's inequality states that the supremum of a positive solution in some connected open region is bounded by some constant times the infimum, possibly with an added term containing a functional normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of the data:
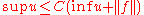
The constant depends on the ellipticity of the equation and the connected open region.
Parabolic partial differential equations
There is a version of Harnack's inequality for linear parabolic PDEs such as heat equationHeat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
.
Let
 be a smooth domain in
be a smooth domain in  and consider the linear parabolic operator
and consider the linear parabolic operatorwith smooth and bounded coefficients and a nondegenerate matrix
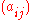 . Suppose that
. Suppose that  is a solution of
is a solution of-
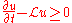 in
in 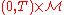
such that
-
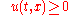 in
in 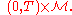
Let
 be a compact subset of
be a compact subset of 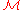 and choose
and choose 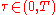 . Then for each
. Then for each  there exists a constant
there exists a constant  (depending only on
(depending only on  ,
,  and the coefficients of
and the coefficients of 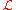 ) such that
) such that