
Hartogs' extension theorem
Encyclopedia
In mathematics, precisely in the theory of functions of several complex variables
, Hartogs' extension theorem is a statement about the singularities of holomorphic function
s of several variables. Informally, it states that the support
of the singularities of such functions cannot be compact
, therefore the singular set of a function of several complex variables must (loosely speaking) 'go off to infinity' in some direction. More precisely, it shows that the concept of isolated singularity and removable singularity coincide for analytic function
s of n > 1 complex variables. A first version of this theorem was proved by Friedrich Hartogs
, and as such it is known also as Hartogs' lemma and Hartogs' principle: in earlier Soviet literature it is also known as the Osgood-Brown theorem, acknowledging later work by Arthur Barton Brown and William Fogg Osgood
. This property of holomorphic functions of several variables is also called Hartogs' phenomenon: however, the locution "Hartogs' phenomenon" is also used to identify the property of solutions of systems of partial differential
or convolution equations satisfying Hartogs type theorems.
in 1906, using Cauchy's integral formula
for functions of several complex variables
. Today, usual proofs rely on either Bochner–Martinelli–Koppelman formula or the solution of the inhomogeneous Cauchy–Riemann equations with compact support. The latter approach is due to Leon Ehrenpreis
who initiated it in the paper . Yet another very simple proof of this result was given by Gaetano Fichera
in the paper , by using his solution of the Dirichlet problem
for holomorphic function
s of several variables and the related concept of CR-function: later he extended the theorem to a certain class of partial differential operators in the paper , and his ideas were later further explored by Giuliano Bratti. Also the Japanese school
of the theory of partial differential operators worked much on this topic, with notable contributions by Akira Kaneko.
 is a holomorphic function
is a holomorphic function
on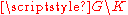 , where
, where  is an open subset of ℂn (with n ≥ 2) and
is an open subset of ℂn (with n ≥ 2) and  is a compact subset of
is a compact subset of  such that
such that 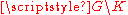 is connected, then
is connected, then  can be extended to a unique holomorphic function on
can be extended to a unique holomorphic function on  .
.
 : to see this, it suffices to consider the function
: to see this, it suffices to consider the function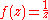
which is clearly holomorphic in ℂ\{ }, but cannot be continued as an holomorphic function on the whole ℂ. Therefore the Hartogs' phenomenon constitutes one elementary phenomena that emphasizes the difference between the theory of functions of one and several complex variables.
}, but cannot be continued as an holomorphic function on the whole ℂ. Therefore the Hartogs' phenomenon constitutes one elementary phenomena that emphasizes the difference between the theory of functions of one and several complex variables.
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, Hartogs' extension theorem is a statement about the singularities of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s of several variables. Informally, it states that the support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of the singularities of such functions cannot be compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, therefore the singular set of a function of several complex variables must (loosely speaking) 'go off to infinity' in some direction. More precisely, it shows that the concept of isolated singularity and removable singularity coincide for analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s of n > 1 complex variables. A first version of this theorem was proved by Friedrich Hartogs
Friedrich Hartogs
Friedrich Moritz Hartogs was a German-Jewish mathematician, known for work on set theory and foundational results on several complex variables.- See also :*Hartogs domain*Hartogs–Laurent expansion...
, and as such it is known also as Hartogs' lemma and Hartogs' principle: in earlier Soviet literature it is also known as the Osgood-Brown theorem, acknowledging later work by Arthur Barton Brown and William Fogg Osgood
William Fogg Osgood
William Fogg Osgood was an American mathematician, born in Boston.In 1886, he graduated from Harvard, where, after studying at the universities of Göttingen and Erlangen , he was instructor , assistant professor , and thenceforth professor of mathematics...
. This property of holomorphic functions of several variables is also called Hartogs' phenomenon: however, the locution "Hartogs' phenomenon" is also used to identify the property of solutions of systems of partial differential
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
or convolution equations satisfying Hartogs type theorems.
Historical note
The original proof was given by Friedrich HartogsFriedrich Hartogs
Friedrich Moritz Hartogs was a German-Jewish mathematician, known for work on set theory and foundational results on several complex variables.- See also :*Hartogs domain*Hartogs–Laurent expansion...
in 1906, using Cauchy's integral formula
Cauchy's integral formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
for functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. Today, usual proofs rely on either Bochner–Martinelli–Koppelman formula or the solution of the inhomogeneous Cauchy–Riemann equations with compact support. The latter approach is due to Leon Ehrenpreis
Leon Ehrenpreis
Leon Ehrenpreis was a mathematician at Temple University who proved the Malgrange–Ehrenpreis theorem, the fundamental theorem about differential operators with constant coefficients....
who initiated it in the paper . Yet another very simple proof of this result was given by Gaetano Fichera
Gaetano Fichera
Gaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
in the paper , by using his solution of the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
for holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s of several variables and the related concept of CR-function: later he extended the theorem to a certain class of partial differential operators in the paper , and his ideas were later further explored by Giuliano Bratti. Also the Japanese school
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
of the theory of partial differential operators worked much on this topic, with notable contributions by Akira Kaneko.
Formal statement
If is a holomorphic function
is a holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on
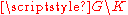 , where
, where  is an open subset of ℂn (with n ≥ 2) and
is an open subset of ℂn (with n ≥ 2) and  is a compact subset of
is a compact subset of  such that
such that 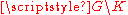 is connected, then
is connected, then  can be extended to a unique holomorphic function on
can be extended to a unique holomorphic function on  .
.Counterexamples in dimension one
The theorem does not hold when : to see this, it suffices to consider the function
: to see this, it suffices to consider the function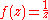
which is clearly holomorphic in ℂ\{
 }, but cannot be continued as an holomorphic function on the whole ℂ. Therefore the Hartogs' phenomenon constitutes one elementary phenomena that emphasizes the difference between the theory of functions of one and several complex variables.
}, but cannot be continued as an holomorphic function on the whole ℂ. Therefore the Hartogs' phenomenon constitutes one elementary phenomena that emphasizes the difference between the theory of functions of one and several complex variables.

