Gaetano Fichera
Encyclopedia
Gaetano Fichera was an Italian mathematician
, working in mathematical analysis
, linear elasticity
, partial differential equation
s and several complex variables
. He was born in Acireale
, and died in Rome.
, a town near Catania
in Sicily: he was the elder of the four sons of Giuseppe Fichera and Marianna Abate. His father Giuseppe was a professor of mathematics
and influenced the young Gaetano starting his life-long passion. In his young years he was a talented football player. On 1 February 1943 he was in the Italian Army
and during the events of September 1943 he was taken prisoner by the Nazist troops, kept imprisoned in Teramo
and then sent to Verona
: he succeeded in escaping from there and reached the Italian region of Emilia-Romagna, spending with partisans the last year of war. After the war he was first in Rome and then in Trieste
, where he met Matelda Colautti, which become his wife in 1952.
in only two years, he entered the University of Catania
at the age of 16, being there from 1937 to 1939 and studying under Pia Nalli. Then he went to the university of Rome
, where in 1941 he earned his laurea
with magna cum laude under the direction of Mauro Picone
, when he was only 19. He was immediately appointed by Picone as an assistant professor to his chair and as a researcher at the Istituto Nazionale per le Applicazioni del Calcolo, becoming his pupil. After the war he went back to Rome working with Mauro Picone
: in 1948 he became "Libero Docente" (free professor) of mathematical analysis
and in 1949 he was appointed as full professor at the University of Trieste
. As he remembers in , in both cases one of the members of the judging commission was Renato Caccioppoli
, which become a close friend of him. From 1956 onward he was full professor at the University of Rome in the chair of mathematical analysis
and then at the Istituto Nazionale di Alta Matematica in the chair of higher analysis, succeeding to Luigi Fantappiè
. He retired from university teaching in 1992, but was professionally very active until his death in 1996: particularly, as a member of the Accademia Nazionale dei Lincei and first director of the journal Rendiconti Lincei – Matematica e Applicazioni he succeeded in reviving the reputation of this publication.
, notably of the Accademia Nazionale dei Lincei, the Accademia Nazionale delle Scienze detta dei XL and of the Russian Academy of Science.
is remembered by him in several occasions. As recalled by , his father Giuseppe was an assistant professor to the chair of Picone while he was teaching at the University of Catania
: they become friends and their friendship lasted even when Giuseppe was forced to leave the academic career for economic reasons, being already the father of two sons, until Giuseppe's death. The young, in effect child, Gaetano, was kept by Picone in his arms. From 1939 to 1941 the young Fichera developed his research directly under the supervision of Picone: as he remembers, it was a time of intense work. But also, when he was back from the front in April 1945 he met Picone while he was in Roma
in his way back to Sicily
, and his advisor was so happy to see him as a father can be seeing its living child. Another mathematician
Fichera was influenced by and acknowledged as one of his teachers and inspirators was Pia Nalli: she was an outstanding analyst
, teaching for several years at the University of Catania
, being his teacher of mathematical analysis
from 1937 to 1939. Antonio Signorini
and Francesco Severi
were two of Fichera's teachers of the Roman period: the first one introduced him and inspired his research in the field of linear elasticity
while the second inspired his research in the field he taught him i.e. the theory of analytic functions of several complex variables
. Signorini had a strong long-time friendship with Picone: on a wall of the apartment building where they lived, in Via delle Tre Madonne, 18 in Rome, a memorial tablet which commemorates the two friends is placed, as recalls. The two great mathematicians extended their friendship to the young Fichera, and as a consequence this led to the solution of the Signorini problem
and the foundation of the theory of variational inequalities. Fichera's relations with Severi were not as friendly as with Signorini and Picone: nevertheless, Severi, which was one of the most influential Italian mathematicians of the first half of the 20th century, esteemed the young mathematician. During a course on the theory of analytic functions of several complex variables
taught at the Istituto Nazionale di Alta Matematica from the fall of 1956 and the beginning of the 1957, whose lectures were collected in the book , Severi posed the problem of generalizing his theorem on the Dirichlet problem
for holomorphic function of several variables
, as recalls: the result was the paper , which is a masterpiece, although not generally acknowledged for various reasons described by . Other scientists he had as teachers during the period 1939–1941 were Enrico Bompiani, Leonida Tonelli
and Giuseppe Armellini: he remembered them with great respect and admiration, even if he did not share all their opinions and ideas, as recalls.
s of the 20th century: Olga Oleinik, Olga Ladyzhenskaya, Israel Gel'fand, Ivan Petrovsky
, Vladimir Maz'ya
, Nikoloz Muskhelishvili, Ilia Vekua
, Richard Courant
, Fritz John
, Kurt Friedrichs, Peter Lax
, Louis Nirenberg
, Ronald Rivlin
, Hans Lewy
, Clifford Truesdell
, Edmund Hlawka
, Ian Sneddon, Jean Leray
, Alexander Weinstein, Alexander Ostrowski
, Renato Caccioppoli
, Solomon Mikhlin
, Paul Naghdi
, Marston Morse
were among his friends, scientific collaborators and correspondents, just to name a few. He build up such a network of contacts being invited several times to lecture on his research by various universities and research institutions, and also participating to several academic conference
s, always upon invitation. This long series of scientific journeys started in 1951, when he went to the USA together with his master and friend Mauro Picone
and Bruno de Finetti
in order to examine the capabilities and characteristics of the first electronic computers and purchase one for the Istituto Nazionale per le Applicazioni del Calcolo: the machine they advised to purchase was the first computer ever working in Italy
. The most complete source about his friends and collaborators is the book by his wife Matelda: in those reference it is also possible to find a fairly complete description of Gaetano Fichera's scientific journeys.
The close fiendship between Angelo Pescarini and Fichera has not his roots in their scientific interests: it is another war story. As recalls, Gaetano, being escaped from Verona
and hidden in a convent
in Alfonsine
, tried to get in touch with the local group of partisans in order to help the people of that town who had been so helpful with him: they were informed about an assistant professor to the chair of higher analysis in Rome who was trying to reach them. Angelo, which was a student of mathematics at the University of Bologna
under Gianfranco Cimmino, a former pupil of Mauro Picone
, was charged of the task of testing the truth of Gaetano's assertions, examining him in mathematics: his question was:– "Mi sai dire una condizione sufficiente per scambiare un limite con un integrale (Can you give me a sufficient condition for interchanging limit and integration)?"–. Gaetano quickly answered:– "Non solo ti darò la condizione sufficiente, ma ti darò anche la condizione necessaria e pure per insiemi non limitati (I can give you not only a sufficiet condition, but also a necessary condition, and not only for bounded domains, but also for unbounded domains)"–. In effect, Fichera proved such a theorem in the paper , his latest paper written in while he was in Rome before joining the army: from that moment on he often used to joke saying that good mathematicians can always have a good application, even for saving one's life.
One of his best friends and appreciated scientific collaborator was Olga Arsenievna Oleinik
: she cured the redaction of his last posthumous paper , as recalls. Also, she used to discuss his work with Gaetano, as he did with her: sometimes their discussion become lively, but nothing more, since they were extremely good friends and estimators of each one's work.
and applied mathematics
listed below. A common characteristic to all of his research is the use of the methods of functional analysis
to prove existence
, uniqueness
and approximation theorems
for the various problems he studied, and also a high consideration of the analytic problems
related to problems in applied mathematics
.
containing a selection of papers presented to the 3rd international symposium on current problems in analysis and mathematical physics, a periodic conference dedicated to Gaetano Fichera.. The biographical entry about Gaetano Fichera at the Enciclopedia Treccani.. Published by the A. Razmadze Mathematical Institute of the Georgian National Academy of Sciences.
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, working in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
, partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s and several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. He was born in Acireale
Acireale
Acireale is a coastal city and commune in the north-east of the province of Catania, Sicily, Italy, at the foot of Mount Etna, on the coast facing the Ionian Sea. It is a diocese, famous for its churches, including the Neo-Gothic St. Peter's Basilica, St...
, and died in Rome.
Biography
He was born in AcirealeAcireale
Acireale is a coastal city and commune in the north-east of the province of Catania, Sicily, Italy, at the foot of Mount Etna, on the coast facing the Ionian Sea. It is a diocese, famous for its churches, including the Neo-Gothic St. Peter's Basilica, St...
, a town near Catania
Catania
Catania is an Italian city on the east coast of Sicily facing the Ionian Sea, between Messina and Syracuse. It is the capital of the homonymous province, and with 298,957 inhabitants it is the second-largest city in Sicily and the tenth in Italy.Catania is known to have a seismic history and...
in Sicily: he was the elder of the four sons of Giuseppe Fichera and Marianna Abate. His father Giuseppe was a professor of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and influenced the young Gaetano starting his life-long passion. In his young years he was a talented football player. On 1 February 1943 he was in the Italian Army
Italian Army
The Italian Army is the ground defence force of the Italian Armed Forces. It is all-volunteer force of active-duty personnel, numbering 108,355 in 2010. Its best-known combat vehicles are the Dardo infantry fighting vehicle, the Centauro tank destroyer and the Ariete tank, and among its aircraft...
and during the events of September 1943 he was taken prisoner by the Nazist troops, kept imprisoned in Teramo
Teramo
Teramo is a city and comune in the central Italian region of Abruzzo, the capital of the province of Teramo.The city, from Rome, is situated between the highest mountains of the Apennines and the Adriatic coast...
and then sent to Verona
Verona
Verona ; German Bern, Dietrichsbern or Welschbern) is a city in the Veneto, northern Italy, with approx. 265,000 inhabitants and one of the seven chef-lieus of the region. It is the second largest city municipality in the region and the third of North-Eastern Italy. The metropolitan area of Verona...
: he succeeded in escaping from there and reached the Italian region of Emilia-Romagna, spending with partisans the last year of war. After the war he was first in Rome and then in Trieste
Trieste
Trieste is a city and seaport in northeastern Italy. It is situated towards the end of a narrow strip of land lying between the Adriatic Sea and Italy's border with Slovenia, which lies almost immediately south and east of the city...
, where he met Matelda Colautti, which become his wife in 1952.
Education and academic career
After graduating from the liceo classicoLiceo classico
Liceo classico is a secondary school type in Italy. The educational curriculum lasts five years, and students are generally about 14 to 19 years of age....
in only two years, he entered the University of Catania
University of Catania
The University of Catania is a university located in Catania, Italy, and founded in 1434. It is the oldest university in Sicily, the 13th oldest in Italy and the 29th oldest university in the world...
at the age of 16, being there from 1937 to 1939 and studying under Pia Nalli. Then he went to the university of Rome
University of Rome La Sapienza
The Sapienza University of Rome, officially Sapienza – Università di Roma, formerly known as Università degli studi di Roma "La Sapienza", is a coeducational, autonomous state university in Rome, Italy...
, where in 1941 he earned his laurea
Laurea
In Italy, the laurea is the main post-secondary academic degree.-Reforms due to the Bologna process:Spurred by the Bologna process, a major reform was instituted in 1999 to introduce easier university degrees comparable to the bachelors...
with magna cum laude under the direction of Mauro Picone
Mauro Picone
Mauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
, when he was only 19. He was immediately appointed by Picone as an assistant professor to his chair and as a researcher at the Istituto Nazionale per le Applicazioni del Calcolo, becoming his pupil. After the war he went back to Rome working with Mauro Picone
Mauro Picone
Mauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
: in 1948 he became "Libero Docente" (free professor) of mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and in 1949 he was appointed as full professor at the University of Trieste
University of Trieste
The University of Trieste is a medium-sized university in Trieste in the Friuli-Venezia Giulia region of Italy. The university consists of 12 faculties, boasts a wide and almost complete range of university courses and currently has about 23,000 students enrolled and 1,000 professors...
. As he remembers in , in both cases one of the members of the judging commission was Renato Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
, which become a close friend of him. From 1956 onward he was full professor at the University of Rome in the chair of mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and then at the Istituto Nazionale di Alta Matematica in the chair of higher analysis, succeeding to Luigi Fantappiè
Luigi Fantappiè
Luigi Fantappiè was an Italian mathematician, known for work in mathematical analysis and for creating the theory of analytic functionals: he was a student and follower of Vito Volterra. Later in life he proposed scientific theories of sweeping scope.He was born in Viterbo, and studied at the...
. He retired from university teaching in 1992, but was professionally very active until his death in 1996: particularly, as a member of the Accademia Nazionale dei Lincei and first director of the journal Rendiconti Lincei – Matematica e Applicazioni he succeeded in reviving the reputation of this publication.
Honours
He was a member of several academiesAcademy
An academy is an institution of higher learning, research, or honorary membership.The name traces back to Plato's school of philosophy, founded approximately 385 BC at Akademia, a sanctuary of Athena, the goddess of wisdom and skill, north of Athens, Greece. In the western world academia is the...
, notably of the Accademia Nazionale dei Lincei, the Accademia Nazionale delle Scienze detta dei XL and of the Russian Academy of Science.
Teachers
His lifelong friendship with his teacher Mauro PiconeMauro Picone
Mauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
is remembered by him in several occasions. As recalled by , his father Giuseppe was an assistant professor to the chair of Picone while he was teaching at the University of Catania
University of Catania
The University of Catania is a university located in Catania, Italy, and founded in 1434. It is the oldest university in Sicily, the 13th oldest in Italy and the 29th oldest university in the world...
: they become friends and their friendship lasted even when Giuseppe was forced to leave the academic career for economic reasons, being already the father of two sons, until Giuseppe's death. The young, in effect child, Gaetano, was kept by Picone in his arms. From 1939 to 1941 the young Fichera developed his research directly under the supervision of Picone: as he remembers, it was a time of intense work. But also, when he was back from the front in April 1945 he met Picone while he was in Roma
Rome
Rome is the capital of Italy and the country's largest and most populated city and comune, with over 2.7 million residents in . The city is located in the central-western portion of the Italian Peninsula, on the Tiber River within the Lazio region of Italy.Rome's history spans two and a half...
in his way back to Sicily
Sicily
Sicily is a region of Italy, and is the largest island in the Mediterranean Sea. Along with the surrounding minor islands, it constitutes an autonomous region of Italy, the Regione Autonoma Siciliana Sicily has a rich and unique culture, especially with regard to the arts, music, literature,...
, and his advisor was so happy to see him as a father can be seeing its living child. Another mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Fichera was influenced by and acknowledged as one of his teachers and inspirators was Pia Nalli: she was an outstanding analyst
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, teaching for several years at the University of Catania
Catania
Catania is an Italian city on the east coast of Sicily facing the Ionian Sea, between Messina and Syracuse. It is the capital of the homonymous province, and with 298,957 inhabitants it is the second-largest city in Sicily and the tenth in Italy.Catania is known to have a seismic history and...
, being his teacher of mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
from 1937 to 1939. Antonio Signorini
Antonio Signorini
- Research activity :His scientific production const of more than 114 works, being papers, monographs and textbooks, 17 of which have been collected in his "Opere Scelte".- Teaching activity :...
and Francesco Severi
Francesco Severi
Francesco Severi was an Italian mathematician.Severi was born in Arezzo, Italy. He is famous for his contributions to algebraic geometry and the theory of functions of several complex variables. He became the effective leader of the Italian school of algebraic geometry...
were two of Fichera's teachers of the Roman period: the first one introduced him and inspired his research in the field of linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
while the second inspired his research in the field he taught him i.e. the theory of analytic functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. Signorini had a strong long-time friendship with Picone: on a wall of the apartment building where they lived, in Via delle Tre Madonne, 18 in Rome, a memorial tablet which commemorates the two friends is placed, as recalls. The two great mathematicians extended their friendship to the young Fichera, and as a consequence this led to the solution of the Signorini problem
Signorini problem
The Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...
and the foundation of the theory of variational inequalities. Fichera's relations with Severi were not as friendly as with Signorini and Picone: nevertheless, Severi, which was one of the most influential Italian mathematicians of the first half of the 20th century, esteemed the young mathematician. During a course on the theory of analytic functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
taught at the Istituto Nazionale di Alta Matematica from the fall of 1956 and the beginning of the 1957, whose lectures were collected in the book , Severi posed the problem of generalizing his theorem on the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
for holomorphic function of several variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, as recalls: the result was the paper , which is a masterpiece, although not generally acknowledged for various reasons described by . Other scientists he had as teachers during the period 1939–1941 were Enrico Bompiani, Leonida Tonelli
Leonida Tonelli
Leonida Tonelli was an Italian mathematician, most noted for creating Tonelli's theorem, usually considered a forerunner to Fubini's theorem.-External links:...
and Giuseppe Armellini: he remembered them with great respect and admiration, even if he did not share all their opinions and ideas, as recalls.
Friends
A complete list of Fichera's friends includes some of the best scientists and mathematicianMathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s of the 20th century: Olga Oleinik, Olga Ladyzhenskaya, Israel Gel'fand, Ivan Petrovsky
Ivan Petrovsky
Ivan Georgievich Petrovsky, also Petrovskii was a Soviet mathematician in the field of partial differential equations, and studied Petrovsky lacunas. He greatly contributed to solution of Hilbert's 19th and 16th problems...
, Vladimir Maz'ya
Vladimir Gilelevich Maz'ya
Vladimir Gilelevich Maz'ya is a Russian mathematician, born in Leningrad in 1937. He made contributions to a wide array of areas of mathematical analysis. He is most well known for his work on Sobolev spaces, and in particular the relationship of Sobolev inequalities and isoperimetry.Maz'ya...
, Nikoloz Muskhelishvili, Ilia Vekua
Ilia Vekua
Ilia Vekua Ilia Vekua Ilia Vekua (Georgian: ილია ვეკუა, ; 23 April 1907 in the village of Sheshelety, Kutais Guberniya, Russian Empire (modern day Ochamchira District, Abkhazia, Republic of Georgia – 2 December 1977 in Tbilisi, USSR) was a distinguished Georgian mathematician, specializing in...
, Richard Courant
Richard Courant
Richard Courant was a German American mathematician.- Life :Courant was born in Lublinitz in the German Empire's Prussian Province of Silesia. During his youth, his parents had to move quite often, to Glatz, Breslau, and in 1905 to Berlin. He stayed in Breslau and entered the university there...
, Fritz John
Fritz John
Fritz John was a German-born mathematician specialising in partial differential equations and ill-posed problems. His early work was on the Radon transform and he is remembered for John's equation.-Biography:...
, Kurt Friedrichs, Peter Lax
Peter Lax
Peter David Lax is a mathematician working in the areas of pure and applied mathematics. He has made important contributions to integrable systems, fluid dynamics and shock waves, solitonic physics, hyperbolic conservation laws, and mathematical and scientific computing, among other fields...
, Louis Nirenberg
Louis Nirenberg
Louis Nirenberg is a Canadian mathematician, and one of the outstanding analysts of the twentieth century. He has made fundamental contributions to linear and nonlinear partial differential equations and their application to complex analysis and geometry.He was born in Hamilton, Ontario and...
, Ronald Rivlin
Ronald Rivlin
Ronald Samuel Rivlin was a British-American physicist, mathematician, rheologist and a noted expert on rubber.-Life:Rivlin was born in London in 1915. He studied physics and mathematics at St John's College, Cambridge, being awarded a BA in 1937 and a ScD in 1952...
, Hans Lewy
Hans Lewy
Hans Lewy was an American mathematician, known for his work on partial differential equations and on the theory of functions of several complex variables....
, Clifford Truesdell
Clifford Truesdell
Clifford Ambrose Truesdell III was an American mathematician, natural philosopher, historian of science, and polemicist.-Life:...
, Edmund Hlawka
Edmund Hlawka
Edmund Hlawka was an Austrian mathematician. He was a leading number theorist. Hlawka did most of his work at the Vienna University of Technology. He was also a visiting professor at Princeton University and the Sorbonne...
, Ian Sneddon, Jean Leray
Jean Leray
Jean Leray was a French mathematician, who worked on both partial differential equations and algebraic topology....
, Alexander Weinstein, Alexander Ostrowski
Alexander Ostrowski
Alexander Markowich Ostrowski , was a mathematician.His father Mark having been a merchant, Alexander Ostrowski attended the Kiev College of Commerce, not a high school, and thus had an insufficient qualification to be admitted to university...
, Renato Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
, Solomon Mikhlin
Solomon Mikhlin
Solomon Grigor'evich Mikhlin was a Soviet mathematician of Jewish origin, working in the fields of linear elasticity, singular integrals and numerical analysis: he is best known for the introduction of the concept of "symbol of a singular integral operator", which eventually led to...
, Paul Naghdi
Paul M. Naghdi
Paul Mansour Naghdi was a professor of mechanical engineering at University of California, Berkeley.He died of lung cancer.-Awards:*George Westinghouse Award of the American Society for Engineering Education...
, Marston Morse
Marston Morse
Harold Calvin Marston Morse was an American mathematician best known for his work on the calculus of variations in the large, a subject where he introduced the technique of differential topology now known as Morse theory...
were among his friends, scientific collaborators and correspondents, just to name a few. He build up such a network of contacts being invited several times to lecture on his research by various universities and research institutions, and also participating to several academic conference
Academic conference
An academic conference or symposium is a conference for researchers to present and discuss their work. Together with academic or scientific journals, conferences provide an important channel for exchange of information between researchers.-Overview:Conferences are usually composed of various...
s, always upon invitation. This long series of scientific journeys started in 1951, when he went to the USA together with his master and friend Mauro Picone
Mauro Picone
Mauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
and Bruno de Finetti
Bruno de Finetti
Bruno de Finetti was an Italian probabilist, statistician and actuary, noted for the "operational subjective" conception of probability...
in order to examine the capabilities and characteristics of the first electronic computers and purchase one for the Istituto Nazionale per le Applicazioni del Calcolo: the machine they advised to purchase was the first computer ever working in Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
. The most complete source about his friends and collaborators is the book by his wife Matelda: in those reference it is also possible to find a fairly complete description of Gaetano Fichera's scientific journeys.
The close fiendship between Angelo Pescarini and Fichera has not his roots in their scientific interests: it is another war story. As recalls, Gaetano, being escaped from Verona
Verona
Verona ; German Bern, Dietrichsbern or Welschbern) is a city in the Veneto, northern Italy, with approx. 265,000 inhabitants and one of the seven chef-lieus of the region. It is the second largest city municipality in the region and the third of North-Eastern Italy. The metropolitan area of Verona...
and hidden in a convent
Convent
A convent is either a community of priests, religious brothers, religious sisters, or nuns, or the building used by the community, particularly in the Roman Catholic Church and in the Anglican Communion...
in Alfonsine
Alfonsine
Alfonsine is a comune in the Province of Ravenna in the Italian region Emilia-Romagna, located about 60 km east of Bologna and about 15 km northwest of Ravenna....
, tried to get in touch with the local group of partisans in order to help the people of that town who had been so helpful with him: they were informed about an assistant professor to the chair of higher analysis in Rome who was trying to reach them. Angelo, which was a student of mathematics at the University of Bologna
University of Bologna
The Alma Mater Studiorum - University of Bologna is the oldest continually operating university in the world, the word 'universitas' being first used by this institution at its foundation. The true date of its founding is uncertain, but believed by most accounts to have been 1088...
under Gianfranco Cimmino, a former pupil of Mauro Picone
Mauro Picone
Mauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
, was charged of the task of testing the truth of Gaetano's assertions, examining him in mathematics: his question was:– "Mi sai dire una condizione sufficiente per scambiare un limite con un integrale (Can you give me a sufficient condition for interchanging limit and integration)?"–. Gaetano quickly answered:– "Non solo ti darò la condizione sufficiente, ma ti darò anche la condizione necessaria e pure per insiemi non limitati (I can give you not only a sufficiet condition, but also a necessary condition, and not only for bounded domains, but also for unbounded domains)"–. In effect, Fichera proved such a theorem in the paper , his latest paper written in while he was in Rome before joining the army: from that moment on he often used to joke saying that good mathematicians can always have a good application, even for saving one's life.
One of his best friends and appreciated scientific collaborator was Olga Arsenievna Oleinik
Olga Arsenievna Oleinik
Olga Arsenievna Oleinik was a Soviet mathematician who conducted pioneering work on the theory of partial differential equations, the theory of strongly inhomogeneous elastic media, and the mathematical theory of boundary layers. She was a student of Ivan Petrovsky...
: she cured the redaction of his last posthumous paper , as recalls. Also, she used to discuss his work with Gaetano, as he did with her: sometimes their discussion become lively, but nothing more, since they were extremely good friends and estimators of each one's work.
Research activity
He is the author of more than 250 papers and 18 books (monographs and course notes): his work concerns mainly the fields of purePure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
and applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
listed below. A common characteristic to all of his research is the use of the methods of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
to prove existence
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
, uniqueness
Uniqueness theorem
The uniqueness theorem for Poisson's equation states that the equation has a unique gradient of the solution for a large class of boundary conditions...
and approximation theorems
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
for the various problems he studied, and also a high consideration of the analytic problems
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
related to problems in applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
.
- Mathematical theory of elasticity and variational inequalities. In the elasticity theory, Fichera is known for the paper where he proves the "Fichera maximum principle", and for his work on variational inequalities, started with the paper , where he announced the existence and uniqueness theoremUniqueness theoremThe uniqueness theorem for Poisson's equation states that the equation has a unique gradient of the solution for a large class of boundary conditions...
for the Signorini problemSignorini problemThe Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...
, and ended with the subsequent ones and , where the full proof was published: those papers are the founding works of the field of variational inequalities, as remarked by Stuart Antman in . Concerning the Saint-Venant's principleSaint-Venant's principleSaint-Venant's principle, named after the French elasticity theorist Jean Claude Barré de Saint-Venant can be stated as saying thatThe original statement was published in French by Saint-Venant in 1855...
, he was able to prove it using a variational approach and a slight variation of a technique employed by Richard Toupin to study the same problem: in the paper there is a complete proof of the principle under the hypothesisHypothesisA hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
that the base of the cylinderCylinder (geometry)A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
is a set with piecewisePiecewiseOn mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
. Also he is known for his researches in the theory of hereditary elasticity: the paper emphasizes the necessity of analyzing very well the constitutive equationConstitutive equationIn physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
s of materials with memory in order to introduce modelsScientific modellingScientific modelling is the process of generating abstract, conceptual, graphical and/or mathematical models. Science offers a growing collection of methods, techniques and theory about all kinds of specialized scientific modelling...
where an existence and uniqueness theoremUniqueness theoremThe uniqueness theorem for Poisson's equation states that the equation has a unique gradient of the solution for a large class of boundary conditions...
s can be proved in a such a way that the proof does not rely on an implicit choice of the topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of the function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
where the problem is studied. At last, it is worth to mention that Clifford Truesdell invited him to write the contributions and for Siegfried FlüggeSiegfried FlüggeSiegfried Flügge was a German theoretical physicist and made contributions to nuclear physics. He worked at the Kaiser-Wilhelm Institut für Chemie and worked in the German Uranverein...
's Handbuch der Physik. - Partial differential equations: he developed an abstract approach through functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
to study general boundary value problemBoundary value problemIn mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s for linear partial differential equations, proving in the paper a theorem similar in spirit to the Lax–Milgram theorem. He studied deeply the mixed boundary value problemMixed boundary conditionIn mathematics, a mixed boundary condition for a partial differential equation indicates that different boundary conditions are used on different parts of the boundary of the domain of the equation....
i.e. a boundary value problemBoundary value problemIn mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
where the boundary has to satisfy a mixed boundary conditionMixed boundary conditionIn mathematics, a mixed boundary condition for a partial differential equation indicates that different boundary conditions are used on different parts of the boundary of the domain of the equation....
: in his first paper on the topic, , he proves the first existence theorem for the mixed boundary problem for self-adjoint operatorSelf-adjoint operatorIn mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s of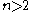
variablesVariable (mathematics)In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, while in the paper he proves the same theorem dropping the hypothesis of self-adjointnessSelf-adjoint operatorIn mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
. He is, according to , the founder of the theory of partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s of non-positive characteristics: in the paper he introduced the now called Fichera's function, in order to identify subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the boundary of the domain where the boundary value problemBoundary value problemIn mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
for such kind of equations is posed, where it is necessary or not to specify the boundary conditionBoundary value problemIn mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
: another account of the theory can be found in the paper , which is written in English and was later translated in Russian and HungarianHungarian languageHungarian is a Uralic language, part of the Ugric group. With some 14 million speakers, it is one of the most widely spoken non-Indo-European languages in Europe....
. - Calculus of variation: his contributions to the calculus of variation are mainly devoted to the proof of existence and uniqueness theoremUniqueness theoremThe uniqueness theorem for Poisson's equation states that the equation has a unique gradient of the solution for a large class of boundary conditions...
s for maxima and minimaMaxima and minimaIn mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
of functionalFunctionalGenerally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
s of particular form, in conjunction with his studies on variational inequalities and linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
in theoretical and applied problems: in the paper a semicontinuity theoremTheoremIn mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
for a functional introduced in the same paper is proved in order to solve the Signorini problemSignorini problemThe Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...
, and this theorem was extended in to the case where the given functionalFunctionalGenerally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
has general linear operators as argumentArgumentIn philosophy and logic, an argument is an attempt to persuade someone of something, or give evidence or reasons for accepting a particular conclusion.Argument may also refer to:-Mathematics and computer science:...
s, not necessarily partial differential operators. - Functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and eigenvalue theory. It is difficult to single out his contributions to functional analysis since, as stated at the beginning of this section, the methods of functional analysis are ubiquitous in his research: however, it is worth to remember paper , where an important existence theorem is proved. His contributions in the field of eigenvalue theory began with the paper , where he formalizes a method developed by Mauro PiconeMauro PiconeMauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
for the approximation of eigenvalues of operators subject only to the condition that their inverseInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
is compactCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
: however, as he admits in , this method does not give any estimate on the approximation error on the value of the calculated (approximated) eigenvalues. He contributed also to the classical eigenvalue problem for symmetric operators, introducing the method of orthogonal invariants: details on this method can be find in , , and references therein. - Approximation theoryApproximation theoryIn mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
. His work in this field is mainly related to the study of systems of functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, possibly being particular solutions of a given partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
or system of such equations, in order to prove their completeness on the boundary of a given domain. The interest of this research is obvious: given such a system of functions, every solution of a boundary value problemBoundary value problemIn mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
can be approximated by an infinite series or Fourier type integral in the topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of a given function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
. One of the most famous examples of this kind of theorem is Mergelyan's theoremMergelyan's theoremMergelyan's theorem is a famous result from complex analysis, a branch of mathematics, named after the Armenian mathematician Sergei Nikitovich Mergelyan and was put forward by him in 1951. It states the following:...
, which completely solves the problem in the class of holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s for a compact set in the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. In his paper , Fichera studies this problem for harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s, relaxing the smoothness requirementsSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
on the boundary in the already cited work : a survey on his and others' work in this area, including contributions of Mauro PiconeMauro PiconeMauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
, Bernard MalgrangeBernard MalgrangeBernard Malgrange is a French mathematician who works on differential equations and singularity theory.He proved the Ehrenpreis–Malgrange theorem and the Malgrange preparation theorem....
, Felix BrowderFelix BrowderFelix E. Browder is a United States mathematician.Felix Browder received his doctorate from Princeton University in 1948. He is known for his research in nonlinear functional analysis, including the theory of semigroups, monotone operators, and fixed points of Cesàro sums of non-expansive operators...
and a number of other mathematicians, is contained in the paper . Another branch of his studies on approximation theoryApproximation theoryIn mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
is strictly tied to complex analysis in one variableComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, and to the already cited Mergelyan's theoremMergelyan's theoremMergelyan's theorem is a famous result from complex analysis, a branch of mathematics, named after the Armenian mathematician Sergei Nikitovich Mergelyan and was put forward by him in 1951. It states the following:...
: he studied the problem of approximating continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on a compact set (and analytic on its interiorInterior (topology)In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
if this is non void) of the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
by rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s with prescribed poles, simple or not. The paper surveys the contribution to the solution of this and related problems by Sergey MergelyanSergey MergelyanSergey Nikitovich Mergelyan was an soviet scientist of Armenian origin, an outstanding mathematician, who is the author of major contributions in Approximation Theory. The modern Complex Approximation Theory is based on Mergelyan's classical work....
, Lennart CarlesonLennart CarlesonLennart Axel Edvard Carleson is a Swedish mathematician, known as a leader in the field of harmonic analysis.-Life:He was a student of Arne Beurling and received his Ph.D. from Uppsala University in 1950...
, Gábor SzegöGábor SzegoGábor Szegő was a Hungarian mathematician. He was one of the foremost analysts of his generation and made fundamental contributions to the theory of Toeplitz matrices and orthogonal polynomials.-Life:...
as well as others, including his own. - Potential theoryPotential theoryIn mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
: his contributions in this field are very important. The results of his paper occupy paragraph 24 of chapter II of the textbook , as remarked by in . Also, his researches and on the asymptotic behaviourAsymptotic analysisIn mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
of the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
near singular pointsSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
of the conducting surface, widely known among the specialists (as several works of V.G. Maz'yaVladimir Gilelevich Maz'yaVladimir Gilelevich Maz'ya is a Russian mathematician, born in Leningrad in 1937. He made contributions to a wide array of areas of mathematical analysis. He is most well known for his work on Sobolev spaces, and in particular the relationship of Sobolev inequalities and isoperimetry.Maz'ya...
, S.A. Nazarov, B.A. Plamenevsky, B.W. Schulze and others testify) can be included in between his works in potential theory. - Measure theory and integration: his main contributions are contained in the papers and . In the first one he proves that a condition on a sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of integrable functions previously introduced by Mauro PiconeMauro PiconeMauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
is both necessary and sufficient in order to assure that limit processLimit (mathematics)In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
and the integration process commute, both in bounded and unboundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
domains: the theorem is similar in spirit to the dominated convergence theoremDominated convergence theoremIn measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
, which however only states a sufficient condition. The second paper contains an extension of the Lebesgue's decomposition theoremLebesgue's decomposition theoremIn mathematics, more precisely in measure theory, Lebesgue's decomposition theorem is a theorem which states that given \mu and \nu two σ-finite signed measures on a measurable space , there exist two σ-finite signed measures \nu_0 and \nu_1 such that:* \nu=\nu_0+\nu_1\, * \nu_0\ll\mu *...
to finitely additive measureMeasure- Legal :* Measure of the Church of England is a law passed by the General Synod and the UK Parliament equivalent of an Act* Measure of the National Assembly for Wales, a law specific to Wales passed by the Welsh Assembly between 2007 and 2011...
s: this extension required him to generalize of the Radon–Nykodim derivative, requiring it to be a set functionSet functionIn mathematics, a set function is a function whose input is a set. The output is usually a number. Often the input is a set of real numbers, a set of points in Euclidean space, or a set of points in some measure space.- Examples :...
belonging to a given class and minimizing a particular functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
. - Complex analysis: he contributed to both the classical topic of complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
in one variable and the more recent one of complex analysis in several variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. His contributions to complex analysis in one variable are essentially approximation resultsApproximation theoryIn mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
, well described in the survey paper (see also the section about his contributions in approximation theory). In the field of functions of several complex variables variables, his contributions were outstanding, but also not generally acknowledged (see the paper for the details). Precisely, he solved the Dirichlet problem for holomorphic function of several variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
under the hypothesis that the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the domain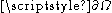
has a Holder continuous normal vector (i.e. it is of 
class) and the Dirichlet boundary conditionDirichlet boundary conditionIn mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
is a functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
belonging to the Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
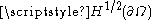satisfying the weak formWeak formulationWeak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
of the tangential Cauchy–Riemann condition (introduced by him) in the paper (see also , where the theorem is presented in English and extended to the case that the normal vector and the Dirichlet boundary condition are only continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
), extending a previous result of Francesco SeveriFrancesco SeveriFrancesco Severi was an Italian mathematician.Severi was born in Arezzo, Italy. He is famous for his contributions to algebraic geometry and the theory of functions of several complex variables. He became the effective leader of the Italian school of algebraic geometry...
: this theorem and the Lewy–Kneser theorem on the localLocal propertyIn mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
Cauchy problemCauchy problemA Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
for holomorphic functions of several variables, laid the foundations of the theory of CR-functions. Another important result is his proof in of an extension of Morera theorem to functions of several complex variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, under the hypothesis that the given functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is only locally integrableLocally integrable functionIn mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
: previous proofs under more restrictive assumptions were given by Francesco SeveriFrancesco SeveriFrancesco Severi was an Italian mathematician.Severi was born in Arezzo, Italy. He is famous for his contributions to algebraic geometry and the theory of functions of several complex variables. He became the effective leader of the Italian school of algebraic geometry...
in and Salomon BochnerSalomon BochnerSalomon Bochner was an American mathematician of Austrian-Hungarian origin, known for wide-ranging work in mathematical analysis, probability theory and differential geometry.- Life :...
in . He also studied the properties of the real part and imaginary part of functions of several complex variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, i.e. pluriharmonic functionPluriharmonic functionIn mathematics, precisely in the theory of functions of several complex variables, a pluriharmonic function is a real valued function which is locally the real part of a holomorphic function of several complex variables. Sometimes a such function is referred as n-harmonic function, where n ≥ 2 is...
s: starting from the paper he gives a trace conditionTrace operatorIn mathematics, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problems, that is, to partial differential equations with prescribed boundary conditions...
analogous to the tangential Cauchy–Riemann condition for the solvability of the Dirichlet problem for pluriharmonic functionPluriharmonic functionIn mathematics, precisely in the theory of functions of several complex variables, a pluriharmonic function is a real valued function which is locally the real part of a holomorphic function of several complex variables. Sometimes a such function is referred as n-harmonic function, where n ≥ 2 is...
s in the paper , and generalizes a theorem of Luigi AmorosoLuigi Amoroso- References : . The first paper where a set of necessary and sufficient conditions for the solvability of the Dirichlet problem for holomorphic functions of several variables is given....
to the complex vector spaceComplex vector spaceA complex vector space is a vector space over the complex numbers. It can also refer to:* a vector space over the real numbers with a linear complex structure...
for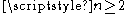 
complex variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
in the paper . Also he was able to prove that a integro-differential equationIntegro-differential equationAn integro-differential equation is an equation which involves both integrals and derivatives of a function.The general first-order, linear integro-differential equation is of the form...
defined on the boundary of a smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
domain by Luigi Amoroso in his cited paper, the Amoroso integro-differential equation, is a necessary and sufficient condition for the solvability of the Dirichlet problem for pluriharmonic functionPluriharmonic functionIn mathematics, precisely in the theory of functions of several complex variables, a pluriharmonic function is a real valued function which is locally the real part of a holomorphic function of several complex variables. Sometimes a such function is referred as n-harmonic function, where n ≥ 2 is...
s when this domain is the sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
in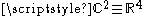
: details can be found in the paper . - Exterior differential forms. His contributions to the theory of differential forms starts as a war story: having read a famous memory of Enrico BettiEnrico Betti-External links:...
(where Betti numberBetti numberIn algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s were introduced) just before joining the army, he used this knowledge in order to develop a theory of exterior differential forms while he was kept prisoner in TeramoTeramoTeramo is a city and comune in the central Italian region of Abruzzo, the capital of the province of Teramo.The city, from Rome, is situated between the highest mountains of the Apennines and the Adriatic coast...
jail. This fact is not uncommon in talented people being kept in captivity, as the known experience of Jean LerayJean LerayJean Leray was a French mathematician, who worked on both partial differential equations and algebraic topology....
with sheaf theory shows. When he was back in Rome in 1945, he discussed his discovery with Enzo MartinelliEnzo MartinelliEnzo Martinelli was an Italian mathematician, working in the theory of functions of several complex variables: he is best known for his work on the theory of integral representations for holomorphic functions of several variables, notably for discovering the Bochner–Martinelli formula in 1938, and...
, who very tactfully informed him that the idea was already developed by mathematicians Élie CartanÉlie CartanÉlie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
and Georges de RhamGeorges de RhamGeorges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
. However, he continued work on this theory, contributing with several papers, and also advised all of his students to study it, despite from the fact of being an analystMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, as he remarks: his main results are collected in the papers and . In the first one he introduced k-measures, a concept less general than currentsCurrent (mathematics)In mathematics, more particularly in functional analysis, differential topology, and geometric measure theory, a k-current in the sense of Georges de Rham is a functional on the space of compactly supported differential k-forms, on a smooth manifold M. Formally currents behave like Schwartz...
but easier to work with: his aim was to clarify the analytic structureMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
of currents and to prove all relevant results of the theory i.e. the three theorems of de RhamDe Rham cohomologyIn mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
and Hodge theorem on harmonic formsHodge theoryIn mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
in a simpler, more analytic way. In the second one he developed an abstract Hodge theoryHodge theoryIn mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
, following the axiomatic method, proving an abstract form of Hodge theorem. - Numerical analysis. As already said in a previous section, his main direct contribution to the field of numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
is the introduction of the method of orthogonal invariants for the calculus of eigenvalues of symmetric operators: however, as already remarked in the introduction to this section, it is hard to find something in his works which is not related to applications. As an example, his works on partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s and linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
have always a constructive aim: for example, the results of paper which deals with the asymptotic analysisAsymptotic analysisIn mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
of the potentialPotential theoryIn mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
were included in the book and led to the definition of the Fichera corner problem as a standard benchmark problemBenchmark (computing)In computing, a benchmark is the act of running a computer program, a set of programs, or other operations, in order to assess the relative performance of an object, normally by running a number of standard tests and trials against it...
for numerical methods. For this aspect, see also the recollections of Wendland in . Another example of his work on quantitative problems is the interdisciplinary work surveyed in . - Biographies and historicalHistory of mathematicsThe area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
studies: his work in this field occupy all the volume . He wrote bibliographical sketches for a number of mathematicians, both teachers, friends and collaborators, including Mauro PiconeMauro PiconeMauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
, Luigi FantappièLuigi FantappièLuigi Fantappiè was an Italian mathematician, known for work in mathematical analysis and for creating the theory of analytic functionals: he was a student and follower of Vito Volterra. Later in life he proposed scientific theories of sweeping scope.He was born in Viterbo, and studied at the...
, Pia Nalli, Maria Adelaide Sneider, Renato CaccioppoliRenato CaccioppoliRenato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
, Solomon MikhlinSolomon MikhlinSolomon Grigor'evich Mikhlin was a Soviet mathematician of Jewish origin, working in the fields of linear elasticity, singular integrals and numerical analysis: he is best known for the introduction of the concept of "symbol of a singular integral operator", which eventually led to...
, Francesco TricomiFrancesco TricomiFrancesco Giacomo Tricomi was an Italian mathematician famous for his studies on mixed type partial differential equations. He was also the author of a book on integral equations....
, Alexander Weinstein, Aldo Ghizzetti. His historicalHistory of mathematicsThe area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
works contain several observations against the so called historical revisitation: the meaning of this concept is clearly stated in the paper . He identifies with the word revisitation the analysis of historical facts basing only on modern conceptions and points of view: this kind of analysis differs from the "true" historical one since it is heavily affected by the historian's point of view. The historian applying this kind of methodology to history of mathematicsHistory of mathematicsThe area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
, and more generally to the history of scienceHistory of scienceThe history of science is the study of the historical development of human understandings of the natural world and the domains of the social sciences....
, emphasizes the sources that have led a field to its modern shape, neglecting the efforts of the pioneers.
Teaching activity
His teaching activity was almost as intense as his research actvity: he also was a pioneer in encouraging gifted women to choose a career in mathematical research, as recalls. An almost complete list of his doctoral students is reported below:See also
- Constitutive equationConstitutive equationIn physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
s - CR-function
- Fichera corner problem
- Mauro PiconeMauro PiconeMauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
- Potential theoryPotential theoryIn mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
- Saint-Venant's principleSaint-Venant's principleSaint-Venant's principle, named after the French elasticity theorist Jean Claude Barré de Saint-Venant can be stated as saying thatThe original statement was published in French by Saint-Venant in 1855...
- Signorini problemSignorini problemThe Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...
- Variational inequalityVariational inequalityIn mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
External links
. A volume of the journal published by the Mathematics Department of the University of CataniaUniversity of Catania
The University of Catania is a university located in Catania, Italy, and founded in 1434. It is the oldest university in Sicily, the 13th oldest in Italy and the 29th oldest university in the world...
containing a selection of papers presented to the 3rd international symposium on current problems in analysis and mathematical physics, a periodic conference dedicated to Gaetano Fichera.. The biographical entry about Gaetano Fichera at the Enciclopedia Treccani.. Published by the A. Razmadze Mathematical Institute of the Georgian National Academy of Sciences.