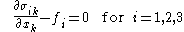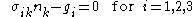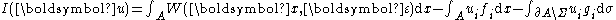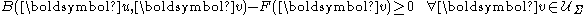Signorini problem
Encyclopedia
The Signorini problem is an elastostatics problem in linear elasticity
: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body
, resting on a rigid
friction
less surface
and subject only to its mass force
s. The name was coined by Gaetano Fichera
to honour his teacher Signorini: the original name coined by him is problem with ambiguous boundary conditions
.
The problem was posed by Antonio Signorini
during a course taught at the Istituto Nazionale di Alta Matematica in 1959, later published as the paper , expanding a previous short exposition he gave in a note published in 1933. According to himself, he called it problem with ambiguous boundary conditions
since there are two alternative sets of boundary conditions
the solution must satisfy on any given contact point, involving not only equalities but also inequalities, but it is not a priori known what of the two sets is satisfied for each point: he asked to determine if the problem is well-posed
or not in a physical sense, i.e. if its solution exists and is unique or not, inviting young analysts
to study the problem. Gaetano Fichera
and Mauro Picone
attended the course, and Fichera started to investigate the existence and uniqueness of the solutions: since there were no references to a similar problem in the theory of boundary value problem
s, he decided to study the problem starting from first principles, precisely from the virtual work principle. While the problem was under investigation, Signorini began to suffer serious health problems: nevertheless, he desidered to know the answer to his question before his death. Picone, being tied by a strong friendship with Signorini, began to chase Fichera to find a solution, who, being himself tied to Signorini by similar feelings, perceived the last months of 1962 as worrying days. Finally, on the first days of January 1963, Fichera was able to give a complete proof of the existence and uniqueness of a solution for the problem with ambiguous boundary condition, which he called "Signorini problem" to honour his teacher. The preliminary note later published as was written up and submitted to Signorini exactly a week before his death: He was very satisfied to see a positive answer to his question. A few days later, he told his family Doctor Damiano Aprile:-"Il mio discepolo Fichera mi ha dato una grande soddisfazione (My disciple Fichera gave me a great contentment)."-"Ma Lei ne ha avute tante, Professore, durante la Sua vita (But you had many, Professor, during your life)"- replied Doctor Aprile, but also Signorini replied:-"Ma questa è la più grande (But this is the greatest one)"-. And those were his last words. According to the solution of the Signorini problem coincides with the birth of the field of variational inequalities
.
in , and also : his derivation of the problem is different from Signorini
's one in that he does not consider only incompressible bodies and a plane rest surface
, as Signorini does. The problem consist in finding the displacement vector from the natural configuration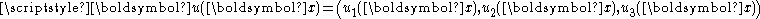
of an anisotropic non-homogeneous elastic body
that lies in a subset
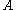of the three-dimension
al euclidean space
whose boundary
is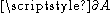
and whose interior normal is the vector 
, resting on a rigid
frictionless surface
whose contact surface
(or more generally contact set) is
and subject only to its body force
s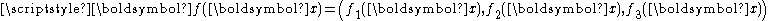
, and surface force
s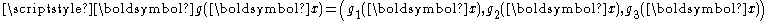
applied on the free (i.e. not in contact with the rest surface) surface 
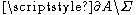: the set 
and the contact surface 
characterize the natural configuration of the body and are known a priori. Therefore the body has to satisfy the general equilibrium equations
written using the Einstein notation
as all in the following development, the ordinary boundary conditions
on
and the following two sets of boundary conditions
on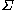
, where 
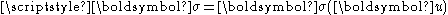is the Cauchy stress tensor. Obviously, the body forces and surface forces cannot be given in arbitrary way but they must satisfy a condition in order for the body to reach an equilibrium configuration: this condition will be deduced and analized in the following development.
is any tangent vector
to the contact set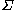
, then the ambiguous boundary condition in each point
of this set are expressed by the following two systems of inequalities
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body
Physical body
In physics, a physical body or physical object is a collection of masses, taken to be one...
, resting on a rigid
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
less surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
and subject only to its mass force
Weight
In science and engineering, the weight of an object is the force on the object due to gravity. Its magnitude , often denoted by an italic letter W, is the product of the mass m of the object and the magnitude of the local gravitational acceleration g; thus:...
s. The name was coined by Gaetano Fichera
Gaetano Fichera
Gaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
to honour his teacher Signorini: the original name coined by him is problem with ambiguous boundary conditions
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
.
History
Antonio Signorini
- Research activity :His scientific production const of more than 114 works, being papers, monographs and textbooks, 17 of which have been collected in his "Opere Scelte".- Teaching activity :...
during a course taught at the Istituto Nazionale di Alta Matematica in 1959, later published as the paper , expanding a previous short exposition he gave in a note published in 1933. According to himself, he called it problem with ambiguous boundary conditions
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
since there are two alternative sets of boundary conditions
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
the solution must satisfy on any given contact point, involving not only equalities but also inequalities, but it is not a priori known what of the two sets is satisfied for each point: he asked to determine if the problem is well-posed
Well-posed problem
The mathematical term well-posed problem stems from a definition given by Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that# A solution exists# The solution is unique...
or not in a physical sense, i.e. if its solution exists and is unique or not, inviting young analysts
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
to study the problem. Gaetano Fichera
Gaetano Fichera
Gaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
and Mauro Picone
Mauro Picone
Mauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
attended the course, and Fichera started to investigate the existence and uniqueness of the solutions: since there were no references to a similar problem in the theory of boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s, he decided to study the problem starting from first principles, precisely from the virtual work principle. While the problem was under investigation, Signorini began to suffer serious health problems: nevertheless, he desidered to know the answer to his question before his death. Picone, being tied by a strong friendship with Signorini, began to chase Fichera to find a solution, who, being himself tied to Signorini by similar feelings, perceived the last months of 1962 as worrying days. Finally, on the first days of January 1963, Fichera was able to give a complete proof of the existence and uniqueness of a solution for the problem with ambiguous boundary condition, which he called "Signorini problem" to honour his teacher. The preliminary note later published as was written up and submitted to Signorini exactly a week before his death: He was very satisfied to see a positive answer to his question. A few days later, he told his family Doctor Damiano Aprile:-"Il mio discepolo Fichera mi ha dato una grande soddisfazione (My disciple Fichera gave me a great contentment)."-"Ma Lei ne ha avute tante, Professore, durante la Sua vita (But you had many, Professor, during your life)"- replied Doctor Aprile, but also Signorini replied:-"Ma questa è la più grande (But this is the greatest one)"-. And those were his last words. According to the solution of the Signorini problem coincides with the birth of the field of variational inequalities
Variational inequality
In mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
.
Formal statement of the problem
The content of this section and the following subsections follows closely the treatment of Gaetano FicheraGaetano Fichera
Gaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
in , and also : his derivation of the problem is different from Signorini
Antonio Signorini
- Research activity :His scientific production const of more than 114 works, being papers, monographs and textbooks, 17 of which have been collected in his "Opere Scelte".- Teaching activity :...
's one in that he does not consider only incompressible bodies and a plane rest surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, as Signorini does. The problem consist in finding the displacement vector from the natural configuration
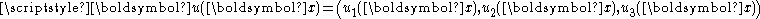of an anisotropic non-homogeneous elastic bodyPhysical body
In physics, a physical body or physical object is a collection of masses, taken to be one...
that lies in a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
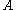of the three-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
whose boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
is
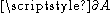and whose interior normal is the vector , resting on a rigidRigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
frictionless surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
whose contact surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
(or more generally contact set) is
and subject only to its body forceBody force
A body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface...
s
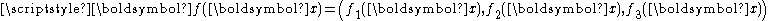, and surface forceSurface force
Surface force denoted fs is the force that acts across an internal or external surface element in a material body. Surface force can be decomposed in to two perpendicular components: pressure and stress forces....
s
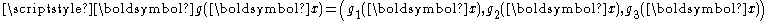applied on the free (i.e. not in contact with the rest surface) surface 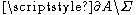: the set and the contact surface characterize the natural configuration of the body and are known a priori. Therefore the body has to satisfy the general equilibrium equations
written using the Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
as all in the following development, the ordinary boundary conditions
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
on
and the following two sets of boundary conditions
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
on
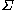, where 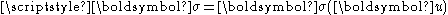is the Cauchy stress tensor. Obviously, the body forces and surface forces cannot be given in arbitrary way but they must satisfy a condition in order for the body to reach an equilibrium configuration: this condition will be deduced and analized in the following development.The ambiguous boundary conditions
If is any tangent vectorTangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
to the contact set
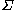, then the ambiguous boundary condition in each pointPoint (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
of this set are expressed by the following two systems of inequalities
or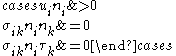
Let's analyze their meaning:- Each set of conditions consists of three relationsBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
, equalities or inequalities, and all the second members are the zero function. - The quantitiesQuantityQuantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
at first member of each first relation are proportionalProportionality (mathematics)In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of the component of the displacement vector directed along the normal vector
. - The quantities at first member of each second relation are proportional to the norm of the component of the tension vector directed along the normal vector
, - The quantities at the first member of each third relation are proportional to the norm of the component of the tension vector along any vector
tangentTangent vectorA tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
in the given pointPoint (geometry)In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
to the contact set
. - The quantities at the first member of each of the three relations are positive if they have the same sense of the vector they are proportionalProportionality (mathematics)In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to, while they are negative if not, therefore the constants of proportionalityProportionality (mathematics)In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
are respectively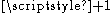
and 
.
Knowing these facts, the set of conditions applies to pointPoint (geometry)In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
s of the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the body which do not leave the contact set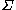
in the equilibrium configuration, since, according to the first relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
, the displacement vector
has no components directed as the normal vector 
, while, according to the second relation, the tension vector may have a component directed as the normal vector 
and having the same sense. In an analogous way, the set of conditions applies to points of the boundary of the body which leave that set in the equilibrium configuration, since displacement vector 
has a component directed as the normal vector 
, while the tension vector has no components directed as the normal vector 
. For both sets of conditions, the tension vector has no tangent component to the contact set, according to the hypothesisHypothesisA hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
that the body rests on a rigid frictionless surface.
Each system expresses a unilateral constraint, in the sense that they express the physical impossibility of the elastic bodyPhysical bodyIn physics, a physical body or physical object is a collection of masses, taken to be one...
to penetrate into the surface where it rests: the ambiguity is not only in the unknown values non-zero quantities must satisfy on the contact set but also in the fact that it is not a priori known if a point belonging to that set satisfies the system of boundary conditions or . The set of points where is satisfied is called the area of support of the elastic body on
, while its complement respect to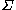 
is called the area of separation.
The above formulation is general since the stress tensorStress tensorStress tensor may refer to:* Stress , in classical physics* Stress-energy tensor, in relativistic theories* Maxwell stress tensor, in electromagnetism...
i.e. the constitutive equationConstitutive equationIn physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
of the elastic bodyPhysical bodyIn physics, a physical body or physical object is a collection of masses, taken to be one...
has not been made explicit: it is equally valid assuming the hypothesisHypothesisA hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
of linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
or the ones of nonlinear elasticity. However, as it would be clear from the following developments, the problem is inherently nonlinear, therefore assuming a linear stress tensor does not simplify the problem.
The form of the stress tensor in the formulation of Signorini and Fichera
The form assumed by SignoriniAntonio Signorini- Research activity :His scientific production const of more than 114 works, being papers, monographs and textbooks, 17 of which have been collected in his "Opere Scelte".- Teaching activity :...
and FicheraGaetano FicheraGaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
for the elastic potential energy is the following one (as in the previous developments, the Einstein notationEinstein notationIn mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
is adopted)
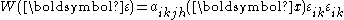
where
is the elasticity tensor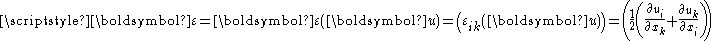
is the infinitesimal strain tensor
The Cauchy stress tensor has therefore the following form
and it is linear with respect to the components of the infinitesimal strain tensor; however, it is not homogeneousHomogeneity (physics)In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...
nor isotropicIsotropyIsotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
.
Solution of the problem
As for the section on the formal statement of the Signorini problem, the contents of this section and the included subsections follow closely the treatment of Gaetano FicheraGaetano FicheraGaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
in , , and also : obviously, the exposition focuses on the basics steps of the proof of the existence and uniqueness for the solution of problem , , , and , rather than the technical details.
The potential energy
The first step of the analysis of Fichera as well as the first step of the analysis of Antonio SignoriniAntonio Signorini- Research activity :His scientific production const of more than 114 works, being papers, monographs and textbooks, 17 of which have been collected in his "Opere Scelte".- Teaching activity :...
in is the analysis of the potential energy, i.e. the following functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
where
belongs to the set of admissible displacements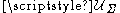 
i.e. the set of displacement vectors satisfying the system of boundary conditionsBoundary value problemIn mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
or . The meaning of each of the three terms is the following- the first one is the total elastic potential energy of the elastic bodyPhysical bodyIn physics, a physical body or physical object is a collection of masses, taken to be one...
- the second one is the total potential energyPotential energyIn physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
due to the body forceBody forceA body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface...
s, for example the gravitational force - the third one is the potential energy due to surface forceSurface forceSurface force denoted fs is the force that acts across an internal or external surface element in a material body. Surface force can be decomposed in to two perpendicular components: pressure and stress forces....
s, for example the forces exerted by the atmospheric pressureAtmospheric pressureAtmospheric pressure is the force per unit area exerted into a surface by the weight of air above that surface in the atmosphere of Earth . In most circumstances atmospheric pressure is closely approximated by the hydrostatic pressure caused by the weight of air above the measurement point...
was able to prove that the admissible displacement
which minimize the integral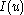 
is a solution of the problem with ambiguous boundary conditions , , , and , provided it is a 
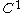functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
supported on the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
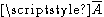of the set 
: however Gaetano FicheraGaetano FicheraGaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
gave a class of counterexampleCounterexampleIn logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
s in showing that in general, admissible displacements are
not smooth functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s of these class. Therefore Fichera tries to minimize the functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
in a wider function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
: in doing so, he first calculates the first variationFirst variationIn applied mathematics and the calculus of variations, the first variation of a functional J is defined as the linear functional \delta J mapping the function h to...
(or functional derivativeFunctional derivativeIn mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
) of the given functional in the neighbourhood of the sought minimizing admissible displacement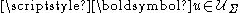
, and then requires it to be greater than or equal to zero
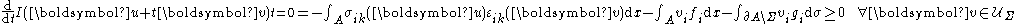
Defining the following functionals
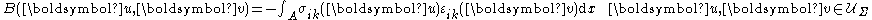
and
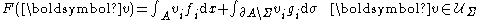
the preceding inequality is can be written as
This inequality is the variational inequalityVariational inequalityIn mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
for the Signorini problem.- Each set of conditions consists of three relations
