
Pluriharmonic function
Encyclopedia
In mathematics
, precisely in the theory of functions of several complex variables
, a pluriharmonic function is a real valued
function
which is locally
the real part of a holomorphic function of several complex variables
. Sometimes a such function is referred as -harmonic function, where
-harmonic function, where  ≥ 2 is the dimension of the complex domain where the function is defined. However, in modern expositions of the theory of functions of several complex variables
≥ 2 is the dimension of the complex domain where the function is defined. However, in modern expositions of the theory of functions of several complex variables
it is preferred to give an equivalent formulation of the concept, by defining pluriharmonic function a complex valued
function whose restriction to every complex
line
is an harmonic function
respect to the real and imaginary part of the complex
line parameter.
 ⊆ ℂn be a complex domain and
⊆ ℂn be a complex domain and 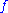 :
:  → ℂ be a
→ ℂ be a 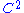 (twice continuously differentiable
(twice continuously differentiable
) function. The function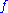 is called pluriharmonic if, for every complex
is called pluriharmonic if, for every complex
line
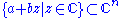
formed by using every couple of complex tuple
s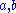 ∈ ℂn, the function
∈ ℂn, the function
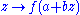
is a harmonic function
on the set
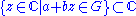 .
.
, but not the other way around. Further, it can be shown that for holomorphic function
s of several complex variables the real (and the imaginary) parts are locally pluriharmonic functions. However a function being harmonic in each variable separately does not imply that it is pluriharmonic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, precisely in the theory of functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, a pluriharmonic function is a real valued
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which is locally
Local property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
the real part of a holomorphic function of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. Sometimes a such function is referred as
 -harmonic function, where
-harmonic function, where  ≥ 2 is the dimension of the complex domain where the function is defined. However, in modern expositions of the theory of functions of several complex variables
≥ 2 is the dimension of the complex domain where the function is defined. However, in modern expositions of the theory of functions of several complex variablesSeveral complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
it is preferred to give an equivalent formulation of the concept, by defining pluriharmonic function a complex valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
function whose restriction to every complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
is an harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
respect to the real and imaginary part of the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
line parameter.
Formal definition
. Let ⊆ ℂn be a complex domain and
⊆ ℂn be a complex domain and 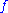 :
:  → ℂ be a
→ ℂ be a 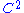 (twice continuously differentiable
(twice continuously differentiableDifferentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
) function. The function
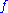 is called pluriharmonic if, for every complex
is called pluriharmonic if, for every complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
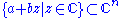
formed by using every couple of complex tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s
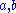 ∈ ℂn, the function
∈ ℂn, the function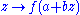
is a harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
on the set
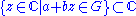 .
.Basic properties
Every pluriharmonic function is a harmonic functionHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
, but not the other way around. Further, it can be shown that for holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s of several complex variables the real (and the imaginary) parts are locally pluriharmonic functions. However a function being harmonic in each variable separately does not imply that it is pluriharmonic.

