Solomon Mikhlin
Encyclopedia
Solomon Grigor'evich Mikhlin (the family name
is also transliterated
as Mihlin or Michlin) (23 April 1908 – 29 August 1990) was a Soviet mathematician
of Jewish origin, working in the fields of linear elasticity
, singular integral
s and numerical analysis
: he is best known for the introduction of the concept of "symbol of a singular integral operator", which eventually led to the foundation and development of the theory of pseudodifferential operators. He was born in Kholmech, a Belarus
ian village, and died in Saint Petersburg
(former Leningrad).
, at a primary religious school (kheder
), and that the family was of modest means: according to the same source, Zalman was the youngest of five children. His first wife was Victoria Isaevna Libina: the famous book is dedicated to her memory. She died of peritonitis
in 1961 during a boat trip on Volga: apparently, there had been doctor on board. In 1940 they adopted a son, Grigory Zalmanovich Mikhlin, who currently lives in Haifa
, Israel. His second wife was Eugenia Yakovlevna Rubinova, born in 1918, who was his companion for the rest of his life.
in 1925. In 1927 he was transferred to the Department of Mathematics and Mechanics of Leningrad State University as a second year student, passing all the exams of the first year without attending lectures. Among his university professors there were Nikolai Maximovich Günther and Vladimir Ivanovich Smirnov
. The latter became his master thesis supervisor: the topic of the thesis was the convergence of double series
, and was defended in 1929. Sergei Lvovich Sobolev
studied in the same class as Mikhlin. In 1930 he started his teaching career, working in some Leningrad
institutes for short periods, as Mikhlin himself records on the document . In 1932 he got a position at the Seismological Institute of the USSR Academy of Sciences, where he worked till 1941: in 1935 he got the degree "Doktor nauk
" in Mathematics
and Physics
, without having to earn the "kandidat nauk" degree, and finally in 1937 he was promoted to the rank of professor. During World War II he became professor at the Kazakh University
in Alma Ata. Since 1944 S.G. Mikhlin has been professor at the Leningrad State University. From 1964 to 1986 he headed the Laboratory of Numerical Methods at the Research Institute of Mathematics and Mechanics of the same university: since 1986 until his death he was a senior researcher at that laboratory.
by the Karl-Marx-Stadt (now Chemnitz
) Polytechnic
in 1968 and was elected member of the German Academy of Sciences Leopoldina in 1970 and of the Accademia Nazionale dei Lincei in 1981. As states, in his country he did not receive honours comparable to his scientific stature, mainly because of the racial policy of the communist regime, briefly described in the following section.
was one of the main themes of that period. Local administrators and communist party
functionaries interfered with scientists on either ethnical
or ideological
grounds. As a matter of fact, during the war and during the creation of a new academic system, Mikhlin did not experienced the same difficulties as younger soviet scientists of Jewish origin: for example he was included in the Soviet delegation in 1958, at the International Congress of Mathematicians
in Edinburgh. However, , examining the life of Mikhlin, finds it surprisingly similar to the life of Vito Volterra
under the fascist regime. He notes that antisemitism in communist countries
took different forms compared to his nazist
counterpart: the communist regime aimed not to the brutal homicide
of Jews, but imposed on them a number of constrictions, sometimes very cruel, in order to make their life difficult. During the period from 1963 to 1981, he met Mikhlin attending several conferences
in the Soviet Union
, and realised how he was in a state of isolation, almost marginalized inside his native community: Fichera
describes several episodes revealing this fact. Perhaps, the most illuminating one is the election of Mikhlin as a member of the Accademia Nazionale dei Lincei: in June 1981, Solomon G. Mikhlin was elected Foreign Member of the class of mathematical
and physical sciences of the Accademia
. At first time, he was proposed as a winner of the Antonio Feltrinelli Prize
, but the almost sure confiscation of the prize by the Soviet authorities induced the Lincei members to elect him as a the member: they decided to honour him in a way that no political authority could alienate, as reports. However, as remembers, Mikhlin was not allowed to visit Italy by the Soviet authorities, so Fichera and his wife brought the tiny golden lynx
, the symbol of the Lincei membership, directly to Mikhlin's apartment in Leningrad
on 17 October 1981: the only guests to that "ceremony
" were Vladimir Maz'ya and his wife Tatyana Shaposhnikova
.
s and textbook
s which become classics for their style. His research is devoted mainly to the following fields.
Green's function
and the reduction of the related boundary value problem
to integral equation
s. The second method is a certain generalization of the classical Schwarz algorithm for the solution of the Dirichlet problem
in a given domain by splitting it in simpler problems in smaller domains whose union
is the original one. Mikhlin studied its convergence and gave applications to special applied problems. He proved existence theorems for the fundamental problems of plane elasticity involving inhomogeneous
anisotropic
media: these results are collected in the book . Concerning the theory of shells, there are several Mikhlin's articles dealing with it. He studied the error of the approximate solution for shells, similar to plane plates, and found out that this error is small for the so called purely rotational state of stress. As a result of his study of this ploblem, Mikhlin also gave a new (invariant
) form of the basic equations of the theory. He also proved a theorem on perturbations
of positive operators in a Hilbert space
which let him to obtain an error estimate for the problem of approximating a sloping shell by a plane plate: the references pertaining to this work are and . Mikhlin studied also the spectrum
of the operator pencil of the classical linear elastostatic operator or Navier–Cauchy operator
where
is the displacement vector, 
is the vector laplacian
,
is the gradient
,
is the divergence
and
is a Cosserat eigenvalue. The full description of the spectrum
and the proof of the completeness
of the system of eigenfunction
s are also due to Mikhlin, and partly to V.G. Maz'ya
in their only joint work. For a historical survey of this problem, including more recent development, see : the work of Mikhlin and his collaborators is summarized in the paper .
theory of singular integral
s, jointly with Francesco Tricomi
and Georges Giraud
, and also one of the main contributors. By singular integral
we mean an integral operator of the following form
where
∈ℝn is a point in the n-dimensional
euclidean space
,
=|
| and 
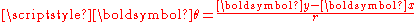are the hyperspherical coordinates (or the polar coordinates or the spherical coordinates respectively when 
or 
) of the point
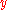with respect to the point 
. Such operators are called singular since the singularity of the kernel of the operator is so strong that the integral does not exists in the ordinary sense, but only in the sense of Cauchy principal value
. Mikhlin was the first to develop a theory of singular integral equations as a theory of operator equations in function space
s. In the papers and he found a rule for the composition of double singular integrals (i.e. in 2-dimensional euclidean space
s) and introduced the very important notion of symbol of a singular integral. This enabled him to show that the algebra of bounded singular integral operators
is isomorphic
to the algebra
of either scalar
or matrix-valued function
s. He proved the Fredholm's theorems for singular integral equations and systems of such equations under the hypothesis of non-degeneracy of the symbol: he also proved that the index of a single singular integral equation in the euclidean space
is zero. In 1961 Mikhlin developed a theory of multidimensional singular integral equations on Lipschitz spaces
. These spaces are widely used in the theory of one-dimensional singular integral equations: however, the direct extension of the related theory to the multidimensional case meets some technical difficulties, and Mikhlin suggested another approach to this problem. Precisely, he obtained the basic properties of this kind of singular integral equations as a by-product of the Lp-space
theory of these equations. Mikhlin also proved a now classical theorem on multipliers of Fourier transform
in the Lp-space
, based on an analogous theorem of Józef Marcinkiewicz
on Fourier series
. A complete collection of his results in this field up to the 1965, as well as the contributions of other mathematicians like Tricomi
, Giraud
, Calderón
and Zygmund
, is contained in the monograph : also, the treatise contains a lot of informations on this field, and an exposition of both the one-dimensional and the multidimensional theory.
A synthesis of the theories of singular integrals and linear partial differential operators was accomplished, in the mid sixties of the 20th century, by the theory of pseudodifferential operators: Joseph J. Kohn
, Louis Nirenberg
, Lars Hörmander
and others operated this synthesis, but this theory owe his rise to the discoveries of Mikhlin, as is universally acknowledged. This theory has numerous applications to mathematical physics
. Mikhlin's multiplier theorem is widely used in different branches of mathematical analysis
, particularly to the theory of differential equation
s. The analysis of Fourier multipliers was later forwarded by Lars Hörmander
, Walter Littman, Elias Stein, Charles Fefferman
and others.
to the mixed problem for the wave equation
. In particular, he solves the mixed problem for the two-space dimensional wave equation
in the half plane
by reducing it to the planar Abel integral equation. For plane domains with a sufficiently smooth
curvilinear
boundary
he reduces the problem to an integro-differential equation
, which he is also able to solve when the boundary of the given domain is analytic
. In 1951 Mikhlin proved the convergence of the Schwarz alternating method
for second order elliptic equations. He also applied the methods of functional analysis
, at the same time as Mark Vishik but independently of him, to the investigation of boundary value problem
s for degenerate second order elliptic partial differential equations.
. Both "a priori" and "a posteriori" estimates of the errors concerning the approximation
given by these methods are proved. The second branch deals with the notion of stability of a numerical process
introduced by Mikhlin himself. When applied to the variational method, this notion enables him to state necessary and sufficient conditions in order to minimize errors in the solution of the given problem when the error arising in the numerical construction of the algebraic system resulting from the application of the method itself is sufficiently small, no matter how large is the system's order. The third branch is the study of variational-difference
and finite element method
s. Mikhlin studied the completeness of the coordinate functions used in this methods in the Sobolev space
, deriving the order of approximation as a function
of the smoothness properties
of the functions to be approximation of functions approximated
. He also characterized the class of coordinate functions which give the best order of approximation, and has studied the stability
of the variational-difference process
and the growth of the condition number
of the variation-difference matrix
. Mikhlin also studied the finite element
approximation in weighted
Sobolev space
s related to the numerical solution of degenerate elliptic equations. He found the optimal order of approximation for some methods of solution of variational inequalities
. The fourth branch of his research in numerical mathematics is a method for the solution of Fredholm integral equation
s which he called resolvent method: its essence rely on the possibility of substituting the kernel of the integral operator by its variational-difference approximation, so that the resolvent of the new kernel can be expressed by simple recurrence formulas. This eliminates the need to construct and solve large systems of equations. During his last years, Mikhlin contributed to the theory of errors in numerical processes, proposing the following classification of errors
.
This classification is useful since enables one to develop computational methods adjusted in order to diminish the errors of each particular type, following the divide et impera (divide and rule) principle.
He was also mentor
and friend of Vladimir Maz'ya: he was never his official supervisor
, but his friendship with the young undergraduate Maz'ya had a great influence on shaping his mathematical style.
Family name
A family name is a type of surname and part of a person's name indicating the family to which the person belongs. The use of family names is widespread in cultures around the world...
is also transliterated
Transliteration
Transliteration is a subset of the science of hermeneutics. It is a form of translation, and is the practice of converting a text from one script into another...
as Mihlin or Michlin) (23 April 1908 – 29 August 1990) was a Soviet mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
of Jewish origin, working in the fields of linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
, singular integral
Singular integral
In mathematics, singular integrals are central to harmonic analysis and are intimately connected with the study of partial differential equations. Broadly speaking a singular integral is an integral operator...
s and numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
: he is best known for the introduction of the concept of "symbol of a singular integral operator", which eventually led to the foundation and development of the theory of pseudodifferential operators. He was born in Kholmech, a Belarus
Belarus
Belarus , officially the Republic of Belarus, is a landlocked country in Eastern Europe, bordered clockwise by Russia to the northeast, Ukraine to the south, Poland to the west, and Lithuania and Latvia to the northwest. Its capital is Minsk; other major cities include Brest, Grodno , Gomel ,...
ian village, and died in Saint Petersburg
Saint Petersburg
Saint Petersburg is a city and a federal subject of Russia located on the Neva River at the head of the Gulf of Finland on the Baltic Sea...
(former Leningrad).
Biography
He was born in Kholmech on 23 April 1908: the document states that his father was a small commerciant, but this assertion could be untrue, since people sometimes lied on the profession of parents in order to overcome political limitatons in the access to higher education. A different version, reported by , states that he was a melamedMelamed
See also:Melamed Melamed, Melammed is a term which in Biblical times denoted a religious teacher or instructor in general , but which in the Talmudic period was applied especially to a teacher of children, and was almost invariably followed by the word "tinokot"...
, at a primary religious school (kheder
Cheder
A Cheder is a traditional elementary school teaching the basics of Judaism and the Hebrew language.-History:...
), and that the family was of modest means: according to the same source, Zalman was the youngest of five children. His first wife was Victoria Isaevna Libina: the famous book is dedicated to her memory. She died of peritonitis
Peritonitis
Peritonitis is an inflammation of the peritoneum, the serous membrane that lines part of the abdominal cavity and viscera. Peritonitis may be localised or generalised, and may result from infection or from a non-infectious process.-Abdominal pain and tenderness:The main manifestations of...
in 1961 during a boat trip on Volga: apparently, there had been doctor on board. In 1940 they adopted a son, Grigory Zalmanovich Mikhlin, who currently lives in Haifa
Haifa
Haifa is the largest city in northern Israel, and the third-largest city in the country, with a population of over 268,000. Another 300,000 people live in towns directly adjacent to the city including the cities of the Krayot, as well as, Tirat Carmel, Daliyat al-Karmel and Nesher...
, Israel. His second wife was Eugenia Yakovlevna Rubinova, born in 1918, who was his companion for the rest of his life.
Education and academic career
According to , he graduated from a secondary school in Gomel in 1923 and entered the State Herzen Pedagogical InstituteHerzen University
The State Russian Herzen Pedagogical University is one of the largest universities in Russia. Located in Saint Petersburg, it operates 20 faculties and more than 100 departments. Embroidered in its structure are the Institute of Pre-University Courses, the Institute of Continuous Professional...
in 1925. In 1927 he was transferred to the Department of Mathematics and Mechanics of Leningrad State University as a second year student, passing all the exams of the first year without attending lectures. Among his university professors there were Nikolai Maximovich Günther and Vladimir Ivanovich Smirnov
Vladimir Ivanovich Smirnov (mathematician)
Vladimir Ivanovich Smirnov was a Russian mathematician who made significant contributions in both pure and applied mathematics, and also in the history of mathematics....
. The latter became his master thesis supervisor: the topic of the thesis was the convergence of double series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, and was defended in 1929. Sergei Lvovich Sobolev
Sergei Lvovich Sobolev
Sergei Lvovich Sobolev was a Soviet mathematician working in mathematical analysis and partial differential equations. He was born in St. Petersburg, and died in Moscow.-Work:...
studied in the same class as Mikhlin. In 1930 he started his teaching career, working in some Leningrad
Leningrad
Leningrad is the former name of Saint Petersburg, Russia.Leningrad may also refer to:- Places :* Leningrad Oblast, a federal subject of Russia, around Saint Petersburg* Leningrad, Tajikistan, capital of Muminobod district in Khatlon Province...
institutes for short periods, as Mikhlin himself records on the document . In 1932 he got a position at the Seismological Institute of the USSR Academy of Sciences, where he worked till 1941: in 1935 he got the degree "Doktor nauk
Doktor nauk
Doktor nauk is a higher doctoral degree, the second and the highest post-graduate academic degree in the Soviet Union, Russia and in many post-Soviet states. Sometimes referred to as Dr. Hab. The prerequisite is the first degree, Kandidat nauk which is informally regarded equivalent to Ph.D....
" in Mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and Physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, without having to earn the "kandidat nauk" degree, and finally in 1937 he was promoted to the rank of professor. During World War II he became professor at the Kazakh University
Abai University
Abai University is one of the leading institutes in Central Asia. It is situated in the heart of Almaty City, Kazakhstan. In 2003 Abai University had a record enrollment of more than 23000 students, mostly from Kazakhstan and other Central Asian countries....
in Alma Ata. Since 1944 S.G. Mikhlin has been professor at the Leningrad State University. From 1964 to 1986 he headed the Laboratory of Numerical Methods at the Research Institute of Mathematics and Mechanics of the same university: since 1986 until his death he was a senior researcher at that laboratory.
Honours
He received the order of the Badge of Honour in 1961: the name of the recipients of this prize was usually published in newspapers. He was awarded of the Laurea honoris causaHonorary degree
An honorary degree or a degree honoris causa is an academic degree for which a university has waived the usual requirements, such as matriculation, residence, study, and the passing of examinations...
by the Karl-Marx-Stadt (now Chemnitz
Chemnitz
Chemnitz is the third-largest city of the Free State of Saxony, Germany. Chemnitz is an independent city which is not part of any county and seat of the government region Direktionsbezirk Chemnitz. Located in the northern foothills of the Ore Mountains, it is a part of the Saxon triangle...
) Polytechnic
Institute of technology
Institute of technology is a designation employed in a wide range of learning institutions awarding different types of degrees and operating often at variable levels of the educational system...
in 1968 and was elected member of the German Academy of Sciences Leopoldina in 1970 and of the Accademia Nazionale dei Lincei in 1981. As states, in his country he did not receive honours comparable to his scientific stature, mainly because of the racial policy of the communist regime, briefly described in the following section.
Influence of communist antisemitism
He lived in one of the most difficult periods of contemporary Russian history. The state of mathematical sciences during this period is well described by : marxist ideology rise in the USSR universities and AcademiaAcademia
Academia is the community of students and scholars engaged in higher education and research.-Etymology:The word comes from the akademeia in ancient Greece. Outside the city walls of Athens, the gymnasium was made famous by Plato as a center of learning...
was one of the main themes of that period. Local administrators and communist party
Communist Party of the Soviet Union
The Communist Party of the Soviet Union was the only legal, ruling political party in the Soviet Union and one of the largest communist organizations in the world...
functionaries interfered with scientists on either ethnical
Ethnic group
An ethnic group is a group of people whose members identify with each other, through a common heritage, often consisting of a common language, a common culture and/or an ideology that stresses common ancestry or endogamy...
or ideological
Ideology
An ideology is a set of ideas that constitutes one's goals, expectations, and actions. An ideology can be thought of as a comprehensive vision, as a way of looking at things , as in common sense and several philosophical tendencies , or a set of ideas proposed by the dominant class of a society to...
grounds. As a matter of fact, during the war and during the creation of a new academic system, Mikhlin did not experienced the same difficulties as younger soviet scientists of Jewish origin: for example he was included in the Soviet delegation in 1958, at the International Congress of Mathematicians
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
in Edinburgh. However, , examining the life of Mikhlin, finds it surprisingly similar to the life of Vito Volterra
Vito Volterra
Vito Volterra was an Italian mathematician and physicist, known for his contributions to mathematical biology and integral equations....
under the fascist regime. He notes that antisemitism in communist countries
Communism
Communism is a social, political and economic ideology that aims at the establishment of a classless, moneyless, revolutionary and stateless socialist society structured upon common ownership of the means of production...
took different forms compared to his nazist
Nazism
Nazism, the common short form name of National Socialism was the ideology and practice of the Nazi Party and of Nazi Germany...
counterpart: the communist regime aimed not to the brutal homicide
Homicide
Homicide refers to the act of a human killing another human. Murder, for example, is a type of homicide. It can also describe a person who has committed such an act, though this use is rare in modern English...
of Jews, but imposed on them a number of constrictions, sometimes very cruel, in order to make their life difficult. During the period from 1963 to 1981, he met Mikhlin attending several conferences
Academic conference
An academic conference or symposium is a conference for researchers to present and discuss their work. Together with academic or scientific journals, conferences provide an important channel for exchange of information between researchers.-Overview:Conferences are usually composed of various...
in the Soviet Union
Soviet Union
The Soviet Union , officially the Union of Soviet Socialist Republics , was a constitutionally socialist state that existed in Eurasia between 1922 and 1991....
, and realised how he was in a state of isolation, almost marginalized inside his native community: Fichera
Gaetano Fichera
Gaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
describes several episodes revealing this fact. Perhaps, the most illuminating one is the election of Mikhlin as a member of the Accademia Nazionale dei Lincei: in June 1981, Solomon G. Mikhlin was elected Foreign Member of the class of mathematical
Mathematical sciences
Mathematical sciences is a broad term that refers to those academic disciplines that are primarily mathematical in nature but may not be universally considered subfields of mathematics proper...
and physical sciences of the Accademia
Accademia
The Accademia is a museum gallery of pre-19th century art in Venice, northern Italy. Situated on the south bank of the Grand Canal, within the sestiere of Dorsoduro, it gives its name to one of the three bridges across the canal, the Ponte dell'Accademia, and to the boat landing station for the...
. At first time, he was proposed as a winner of the Antonio Feltrinelli Prize
Antonio Feltrinelli Prize
The Antonio Feltrinelli Prize is a prestigious award for achievement in the arts, music, literature, history, philosophy, medicine, and physical and mathematical sciences. The award comes with a monetary grant, a certificate, and a gold medal. The prize is awarded once every five years in each...
, but the almost sure confiscation of the prize by the Soviet authorities induced the Lincei members to elect him as a the member: they decided to honour him in a way that no political authority could alienate, as reports. However, as remembers, Mikhlin was not allowed to visit Italy by the Soviet authorities, so Fichera and his wife brought the tiny golden lynx
Lynx
A lynx is any of the four Lynx genus species of medium-sized wildcats. The name "lynx" originated in Middle English via Latin from Greek word "λύγξ", derived from the Indo-European root "*leuk-", meaning "light, brightness", in reference to the luminescence of its reflective eyes...
, the symbol of the Lincei membership, directly to Mikhlin's apartment in Leningrad
Leningrad
Leningrad is the former name of Saint Petersburg, Russia.Leningrad may also refer to:- Places :* Leningrad Oblast, a federal subject of Russia, around Saint Petersburg* Leningrad, Tajikistan, capital of Muminobod district in Khatlon Province...
on 17 October 1981: the only guests to that "ceremony
Ceremony
A ceremony is an event of ritual significance, performed on a special occasion. The word may be of Etruscan origin.-Ceremonial occasions:A ceremony may mark a rite of passage in a human life, marking the significance of, for example:* birth...
" were Vladimir Maz'ya and his wife Tatyana Shaposhnikova
Tatyana Shaposhnikova
Tatyana Olegovna Shaposhnikova is a Russian mathematician, working at Linköping University, Sweden. She is best known for her work in the theory of multipliers in function spaces, partial differential operators and history of mathematics, some of which was partly done jointly with Vladimir...
.
Death
According to , which refers a conversation with Mark Vishik and Olga Oleinik, on 29 August 1990 Mikhlin left home to buy medicines for his wife Eugenia. On a public transport, he suffered a lethal stroke. He had no documents with him, therefore he was identified only some time after his death: this may be the cause of the difference in the death date reported on several biographies and obituary notices. Fichera also writes that Mikhlin's wife Eugenia survived him only a few months.Research activity
He was author of monographMonograph
A monograph is a work of writing upon a single subject, usually by a single author.It is often a scholarly essay or learned treatise, and may be released in the manner of a book or journal article. It is by definition a single document that forms a complete text in itself...
s and textbook
Textbook
A textbook or coursebook is a manual of instruction in any branch of study. Textbooks are produced according to the demands of educational institutions...
s which become classics for their style. His research is devoted mainly to the following fields.
Elasticity theory and boundary value problems
In mathematical elasticity theory, Mikhlin was concerned by three themes: the plane problem (mainly from 1932 to 1935), the theory of shells (from 1954) and the Cosserat spectrum (from 1967 to 1973). Dealing with the plane elasticity problem, he proposed two methods for its solution in multiply connected domains. The first one is based upon the so called complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
and the reduction of the related boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
to integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s. The second method is a certain generalization of the classical Schwarz algorithm for the solution of the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
in a given domain by splitting it in simpler problems in smaller domains whose union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
is the original one. Mikhlin studied its convergence and gave applications to special applied problems. He proved existence theorems for the fundamental problems of plane elasticity involving inhomogeneous
Homogeneity (physics)
In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...
anisotropic
Isotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
media: these results are collected in the book . Concerning the theory of shells, there are several Mikhlin's articles dealing with it. He studied the error of the approximate solution for shells, similar to plane plates, and found out that this error is small for the so called purely rotational state of stress. As a result of his study of this ploblem, Mikhlin also gave a new (invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
) form of the basic equations of the theory. He also proved a theorem on perturbations
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
of positive operators in a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
which let him to obtain an error estimate for the problem of approximating a sloping shell by a plane plate: the references pertaining to this work are and . Mikhlin studied also the spectrum
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
of the operator pencil of the classical linear elastostatic operator or Navier–Cauchy operator
where
is the displacement vector, is the vector laplacianVector Laplacian
In mathematics and physics, the vector Laplace operator, denoted by \scriptstyle \nabla^2, named after Pierre-Simon Laplace, is a differential operator defined over a vector field. The vector Laplacian is similar to the scalar Laplacian...
,
is the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
,
is the divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
and
is a Cosserat eigenvalue. The full description of the spectrumSpectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
and the proof of the completeness
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
of the system of eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s are also due to Mikhlin, and partly to V.G. Maz'ya
Vladimir Gilelevich Maz'ya
Vladimir Gilelevich Maz'ya is a Russian mathematician, born in Leningrad in 1937. He made contributions to a wide array of areas of mathematical analysis. He is most well known for his work on Sobolev spaces, and in particular the relationship of Sobolev inequalities and isoperimetry.Maz'ya...
in their only joint work. For a historical survey of this problem, including more recent development, see : the work of Mikhlin and his collaborators is summarized in the paper .
Singular integrals and Fourier multipliers
He is one of the founders of the multi-dimensionalDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
theory of singular integral
Singular integral
In mathematics, singular integrals are central to harmonic analysis and are intimately connected with the study of partial differential equations. Broadly speaking a singular integral is an integral operator...
s, jointly with Francesco Tricomi
Francesco Tricomi
Francesco Giacomo Tricomi was an Italian mathematician famous for his studies on mixed type partial differential equations. He was also the author of a book on integral equations....
and Georges Giraud
Georges Giraud
Georges Giraud was a French mathematician, working in potential theory, partial differential equations, singular integrals and singular integral equations: he is mainly known for his solution of the regular oblique derivative problem and also for his extension to n-dimensional singular integral...
, and also one of the main contributors. By singular integral
Singular integral
In mathematics, singular integrals are central to harmonic analysis and are intimately connected with the study of partial differential equations. Broadly speaking a singular integral is an integral operator...
we mean an integral operator of the following form
where
∈ℝn is a point in the n-dimensionalDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
,
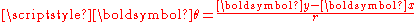=|| and are the hyperspherical coordinates (or the polar coordinates or the spherical coordinates respectively when or ) of the pointPoint
-Business and finance:* Basis point, 1/100 of one percent, denoted bp, bps, and ‱* Pivot point, a price level of significance in analysis of a financial market that is used as a predictive indicator of market movement...
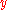with respect to the point . Such operators are called singular since the singularity of the kernel of the operator is so strong that the integral does not exists in the ordinary sense, but only in the sense of Cauchy principal valueCauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
. Mikhlin was the first to develop a theory of singular integral equations as a theory of operator equations in function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s. In the papers and he found a rule for the composition of double singular integrals (i.e. in 2-dimensional euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s) and introduced the very important notion of symbol of a singular integral. This enabled him to show that the algebra of bounded singular integral operators
Operator algebra
In functional analysis, an operator algebra is an algebra of continuous linear operators on a topological vector space with the multiplication given by the composition of mappings...
is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
of either scalar
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
or matrix-valued function
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
s. He proved the Fredholm's theorems for singular integral equations and systems of such equations under the hypothesis of non-degeneracy of the symbol: he also proved that the index of a single singular integral equation in the euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is zero. In 1961 Mikhlin developed a theory of multidimensional singular integral equations on Lipschitz spaces
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
. These spaces are widely used in the theory of one-dimensional singular integral equations: however, the direct extension of the related theory to the multidimensional case meets some technical difficulties, and Mikhlin suggested another approach to this problem. Precisely, he obtained the basic properties of this kind of singular integral equations as a by-product of the Lp-space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
theory of these equations. Mikhlin also proved a now classical theorem on multipliers of Fourier transform
Multiplier (Fourier analysis)
In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a specified function known as the multiplier or symbol...
in the Lp-space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, based on an analogous theorem of Józef Marcinkiewicz
Józef Marcinkiewicz
Józef Marcinkiewicz – died in 1940 in Kharkiv, Ukraine) was a Polish mathematician.He was a student of Antoni Zygmund; and later worked with Juliusz Schauder, and Stefan Kaczmarz. He was a professor of the Stefan Batory University in Wilno....
on Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. A complete collection of his results in this field up to the 1965, as well as the contributions of other mathematicians like Tricomi
Francesco Tricomi
Francesco Giacomo Tricomi was an Italian mathematician famous for his studies on mixed type partial differential equations. He was also the author of a book on integral equations....
, Giraud
Georges Giraud
Georges Giraud was a French mathematician, working in potential theory, partial differential equations, singular integrals and singular integral equations: he is mainly known for his solution of the regular oblique derivative problem and also for his extension to n-dimensional singular integral...
, Calderón
Alberto Calderón
Alberto Pedro Calderón was an Argentine mathematician best known for his work on the theory of partial differential equations and singular integral operators, and widely considered as one of the 20th century's most important mathematicians...
and Zygmund
Antoni Zygmund
Antoni Zygmund was a Polish-born American mathematician.-Life:Born in Warsaw, Zygmund obtained his PhD from Warsaw University and became a professor at Stefan Batory University at Wilno...
, is contained in the monograph : also, the treatise contains a lot of informations on this field, and an exposition of both the one-dimensional and the multidimensional theory.
A synthesis of the theories of singular integrals and linear partial differential operators was accomplished, in the mid sixties of the 20th century, by the theory of pseudodifferential operators: Joseph J. Kohn
Joseph J. Kohn
Joseph John Kohn is a Professor Emeritus of mathematics at Princeton University, where he does research on partial differential operators and function theory.-Life and work:...
, Louis Nirenberg
Louis Nirenberg
Louis Nirenberg is a Canadian mathematician, and one of the outstanding analysts of the twentieth century. He has made fundamental contributions to linear and nonlinear partial differential equations and their application to complex analysis and geometry.He was born in Hamilton, Ontario and...
, Lars Hörmander
Lars Hörmander
Lars Valter Hörmander is a Swedish mathematician who has been called "the foremost contributor to the modern theory of linear partial differential equations". He was awarded the Fields Medal in 1962, and the Wolf Prize in 1988...
and others operated this synthesis, but this theory owe his rise to the discoveries of Mikhlin, as is universally acknowledged. This theory has numerous applications to mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
. Mikhlin's multiplier theorem is widely used in different branches of mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, particularly to the theory of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. The analysis of Fourier multipliers was later forwarded by Lars Hörmander
Lars Hörmander
Lars Valter Hörmander is a Swedish mathematician who has been called "the foremost contributor to the modern theory of linear partial differential equations". He was awarded the Fields Medal in 1962, and the Wolf Prize in 1988...
, Walter Littman, Elias Stein, Charles Fefferman
Charles Fefferman
Charles Louis Fefferman is an American mathematician at Princeton University. His primary field of research is mathematical analysis....
and others.
Partial differential equations
In four papers, published in the period 1940–1942, Mikhlin deals with the application of the potentials methodPotential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
to the mixed problem for the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
. In particular, he solves the mixed problem for the two-space dimensional wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
in the half plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
by reducing it to the planar Abel integral equation. For plane domains with a sufficiently smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
curvilinear
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
he reduces the problem to an integro-differential equation
Integro-differential equation
An integro-differential equation is an equation which involves both integrals and derivatives of a function.The general first-order, linear integro-differential equation is of the form...
, which he is also able to solve when the boundary of the given domain is analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
. In 1951 Mikhlin proved the convergence of the Schwarz alternating method
Schwarz alternating method
In mathematics, the Schwarz alternating method, named after Hermann Schwarz, is an iterative method to find the solution of a partial differential equations on a domain which is the union of two overlapping subdomains, by solving the equation on each of the two subdomains in turn, taking always the...
for second order elliptic equations. He also applied the methods of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, at the same time as Mark Vishik but independently of him, to the investigation of boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s for degenerate second order elliptic partial differential equations.
Numerical mathematics
His work in this field can be divided into several branches: in the following text, four main branches are described, and a sketch of his last researches is also given. The papers within the first branch are summarized in the monograph , which contain the study of convergence of variational methods for problems connected with positive operators, in particular, for some problems of mathematical physicsMathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
. Both "a priori" and "a posteriori" estimates of the errors concerning the approximation
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
given by these methods are proved. The second branch deals with the notion of stability of a numerical process
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
introduced by Mikhlin himself. When applied to the variational method, this notion enables him to state necessary and sufficient conditions in order to minimize errors in the solution of the given problem when the error arising in the numerical construction of the algebraic system resulting from the application of the method itself is sufficiently small, no matter how large is the system's order. The third branch is the study of variational-difference
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
and finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
s. Mikhlin studied the completeness of the coordinate functions used in this methods in the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
, deriving the order of approximation as a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the smoothness properties
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
of the functions to be approximation of functions approximated
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
. He also characterized the class of coordinate functions which give the best order of approximation, and has studied the stability
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
of the variational-difference process
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
and the growth of the condition number
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
of the variation-difference matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Mikhlin also studied the finite element
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
approximation in weighted
Weight function
A weight function is a mathematical device used when performing a sum, integral, or average in order to give some elements more "weight" or influence on the result than other elements in the same set. They occur frequently in statistics and analysis, and are closely related to the concept of a...
Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s related to the numerical solution of degenerate elliptic equations. He found the optimal order of approximation for some methods of solution of variational inequalities
Variational inequality
In mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
. The fourth branch of his research in numerical mathematics is a method for the solution of Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
s which he called resolvent method: its essence rely on the possibility of substituting the kernel of the integral operator by its variational-difference approximation, so that the resolvent of the new kernel can be expressed by simple recurrence formulas. This eliminates the need to construct and solve large systems of equations. During his last years, Mikhlin contributed to the theory of errors in numerical processes, proposing the following classification of errors
Numerical error
In software engineering and mathematics, numerical error is the combined effect of two kinds of error in a calculation. The first is caused by the finite precision of computations involving floating-point or integer values...
.
- Approximation error: is the error due to the replacement of an exact problem by an approximating one.
- Perturbation error: is the error due to the inaccuracies in the computatation of the data of the approximating problem.
- Algorithm error: is the intrinsic error of the algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
used for the solution of the approximating problem. - Rounding error: is the error due to the limits of computer arithmetics.
This classification is useful since enables one to develop computational methods adjusted in order to diminish the errors of each particular type, following the divide et impera (divide and rule) principle.
Teaching activity
He was the "kandidat nauk" advisor of a number of mathematicians: a partial list of them is shown belowHe was also mentor
Mentor
In Greek mythology, Mentor was the son of Alcimus or Anchialus. In his old age Mentor was a friend of Odysseus who placed Mentor and Odysseus' foster-brother Eumaeus in charge of his son Telemachus, and of Odysseus' palace, when Odysseus left for the Trojan War.When Athena visited Telemachus she...
and friend of Vladimir Maz'ya: he was never his official supervisor
Supervisor
A supervisor, foreperson, team leader, overseer, cell coach, facilitator, or area coordinator is a manager in a position of trust in business...
, but his friendship with the young undergraduate Maz'ya had a great influence on shaping his mathematical style.
See also
- Linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
- Mikhlin multiplier theorem
- Multiplier (Fourier analysis)Multiplier (Fourier analysis)In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a specified function known as the multiplier or symbol...
- Singular integralSingular integralIn mathematics, singular integrals are central to harmonic analysis and are intimately connected with the study of partial differential equations. Broadly speaking a singular integral is an integral operator...
s - Singular integral equations