Hereditary set
Encyclopedia
In set theory
, a hereditary set (or pure set) is a set all of whose elements are hereditary sets. That is, all elements of the set are themselves sets, as are all elements of the elements, and so on. For example, it is vacuously true that the empty set is a hereditary set, and thus the set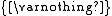
containing only the empty set
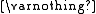is a hereditary set.
In formulations of set theory that are intended to be interpreted in the von Neumann universe
or to express the content of Zermelo–Fraenkel set theory
, all sets are hereditary, because the only sort of object that is even a candidate to be an element of a set is another set. Thus the notion of hereditary set is interesting only in a context in which there may be urelements.
The inductive definition of hereditary sets presupposes that set membership is well-founded
(i.e., the axiom of regularity
), otherwise the recurrence may not have a unique solution. However, it can be restated non-inductively as follows: a set is hereditary if and only if its transitive closure contains only sets.
In this way the concept of hereditary sets can also be extended to non-well-founded set theories in which sets can be members of themselves. For example, a set that contains only itself is a hereditary set.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a hereditary set (or pure set) is a set all of whose elements are hereditary sets. That is, all elements of the set are themselves sets, as are all elements of the elements, and so on. For example, it is vacuously true that the empty set is a hereditary set, and thus the set
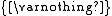containing only the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
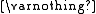is a hereditary set.In formulations of set theory that are intended to be interpreted in the von Neumann universe
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
or to express the content of Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, all sets are hereditary, because the only sort of object that is even a candidate to be an element of a set is another set. Thus the notion of hereditary set is interesting only in a context in which there may be urelements.
The inductive definition of hereditary sets presupposes that set membership is well-founded
Well-founded relation
In mathematics, a binary relation, R, is well-founded on a class X if and only if every non-empty subset of X has a minimal element with respect to R; that is, for every non-empty subset S of X, there is an element m of S such that for every element s of S, the pair is not in R:\forall S...
(i.e., the axiom of regularity
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
), otherwise the recurrence may not have a unique solution. However, it can be restated non-inductively as follows: a set is hereditary if and only if its transitive closure contains only sets.
In this way the concept of hereditary sets can also be extended to non-well-founded set theories in which sets can be members of themselves. For example, a set that contains only itself is a hereditary set.