
Hoare logic
Encyclopedia
Hoare logic is a formal system
with a set of logical rules for reasoning rigorously about the correctness of computer programs. It was proposed in 1969 by the British computer scientist and logician
C. A. R. Hoare
, and subsequently refined by Hoare and other researchers. The original ideas were seeded by the work of Robert Floyd
, who had published a similar system for flowchart
s.

where P and Q are assertions
and C is a command. P is named the precondition and Q the postcondition: when the precondition is met, the command establishes the postcondition. Assertions are formulas in predicate logic
.
Hoare logic provides axiom
s and inference rules for all the constructs of a simple imperative programming language
. In addition to the rules for the simple language in Hoare's original paper, rules for other language constructs have been developed since then by Hoare and many other researchers. There are rules for concurrency
, procedures, jumps, and pointers.
Total correctness can be also proven with an extended version of the While rule.

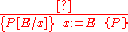
Here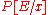 denotes the expression P in which all free occurrence
denotes the expression P in which all free occurrence
s of the variable x have been replaced with the expression E.
The assignment axiom means that the truth of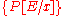 is equivalent to the after-assignment truth of
is equivalent to the after-assignment truth of 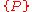 . Thus were
. Thus were 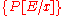 true prior to the assignment, by the assignment axiom, then
true prior to the assignment, by the assignment axiom, then 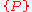 would be true subsequent to which. Conversely, were
would be true subsequent to which. Conversely, were 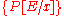 false prior to the assignment statement,
false prior to the assignment statement, 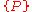 must then be false consequently.
must then be false consequently.
Examples of valid triples include:
The assignment axiom proposed by Hoare does not apply when more than one name may refer to the same stored value. For example,

is not a true statement if x and y refer to the same variable, because no precondition can cause y to be 3 after x is set to 2.
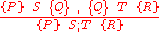
For example, consider the following two instances of the assignment axiom:

and
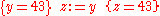
By the sequencing rule, one concludes:

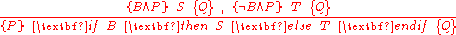
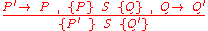
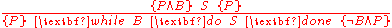
Here P is the loop invariant
.
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
with a set of logical rules for reasoning rigorously about the correctness of computer programs. It was proposed in 1969 by the British computer scientist and logician
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
C. A. R. Hoare
C. A. R. Hoare
Sir Charles Antony Richard Hoare , commonly known as Tony Hoare or C. A. R. Hoare, is a British computer scientist best known for the development of Quicksort, one of the world's most widely used sorting algorithms...
, and subsequently refined by Hoare and other researchers. The original ideas were seeded by the work of Robert Floyd
Robert Floyd
Robert W Floyd was an eminent computer scientist.His contributions include the design of the Floyd–Warshall algorithm , which efficiently finds all shortest paths in a graph, Floyd's cycle-finding algorithm for detecting cycles in a sequence, and his work on parsing...
, who had published a similar system for flowchart
Flowchart
A flowchart is a type of diagram that represents an algorithm or process, showing the steps as boxes of various kinds, and their order by connecting these with arrows. This diagrammatic representation can give a step-by-step solution to a given problem. Process operations are represented in these...
s.
Hoare Triple
The central feature of Hoare logic is the Hoare triple. A triple describes how the execution of a piece of code changes the state of the computation. A Hoare triple is of the form
where P and Q are assertions
Assertion (computing)
In computer programming, an assertion is a predicate placed in a program to indicate that the developer thinks that the predicate is always true at that place.For example, the following code contains two assertions:...
and C is a command. P is named the precondition and Q the postcondition: when the precondition is met, the command establishes the postcondition. Assertions are formulas in predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
.
Hoare logic provides axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s and inference rules for all the constructs of a simple imperative programming language
Imperative programming
In computer science, imperative programming is a programming paradigm that describes computation in terms of statements that change a program state...
. In addition to the rules for the simple language in Hoare's original paper, rules for other language constructs have been developed since then by Hoare and many other researchers. There are rules for concurrency
Concurrency (computer science)
In computer science, concurrency is a property of systems in which several computations are executing simultaneously, and potentially interacting with each other...
, procedures, jumps, and pointers.
Partial and total correctness
Standard Hoare logic proves only partial correctness, while termination needs be proved separately. Thus the intuitive reading of a Hoare triple is: Whenever P holds of the state before the execution of C, then Q will hold afterwards, or C does not terminate. Note that if C does not terminate, then there is no "after", so Q can be any statement at all. Indeed, one can choose Q to be false to express that C does not terminate.Total correctness can be also proven with an extended version of the While rule.
Empty statement axiom schema
The empty statement rule asserts that the skip statement does not change the state of the program, thus whatever holds true before skip also holds true afterwards.
Assignment axiom schema
The assignment axiom states that after the assignment any predicate holds for the variable that was previously true for the right-hand side of the assignment: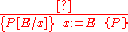
Here
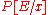 denotes the expression P in which all free occurrence
denotes the expression P in which all free occurrenceFree variables and bound variables
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
s of the variable x have been replaced with the expression E.
The assignment axiom means that the truth of
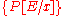 is equivalent to the after-assignment truth of
is equivalent to the after-assignment truth of 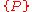 . Thus were
. Thus were 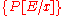 true prior to the assignment, by the assignment axiom, then
true prior to the assignment, by the assignment axiom, then 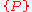 would be true subsequent to which. Conversely, were
would be true subsequent to which. Conversely, were 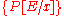 false prior to the assignment statement,
false prior to the assignment statement, 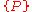 must then be false consequently.
must then be false consequently.Examples of valid triples include:
The assignment axiom proposed by Hoare does not apply when more than one name may refer to the same stored value. For example,

is not a true statement if x and y refer to the same variable, because no precondition can cause y to be 3 after x is set to 2.
Rule of composition
Hoare's rule of composition applies to sequentially-executed programs S and T, where S executes prior to T and is written S;T.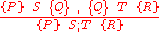
For example, consider the following two instances of the assignment axiom:

and
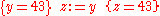
By the sequencing rule, one concludes:

Conditional rule
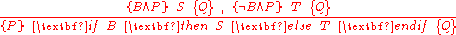
Consequence rule
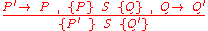
While rule
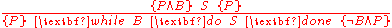
Here P is the loop invariant
Loop invariant
In computer science, a loop invariant is an invariant used to prove properties of loops. Informally, a loop invariant is a statement of the conditions that should be true on entry into a loop and that are guaranteed to remain true on every iteration of the loop...
.
While rule for total correctness
-
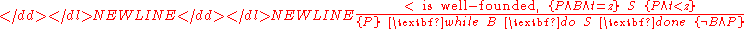
In this rule, in addition to maintaining the loop invariant, one also proves termination by way of a term, called the loop variantLoop variantIn computer science, a loop variant is a mathematical function defined on the state space of a computer program whose value is monotonically decreased with respect to a well-founded relation by the iteration of a while loop under some invariant conditions, thereby ensuring its termination...
, here t, whose value strictly decreases with respect to a well-founded relationWell-founded relationIn mathematics, a binary relation, R, is well-founded on a class X if and only if every non-empty subset of X has a minimal element with respect to R; that is, for every non-empty subset S of X, there is an element m of S such that for every element s of S, the pair is not in R:\forall S...
during each iteration. Note that, given the invariant P, the condition B must imply that t is not a minimal element of its range, for otherwise the premise of this rule would be false. Because the relation "<" is well-founded, each step of the loop is counted by decreasing members of a finite chain. Also note that square brackets are used here instead of curly braces to denote total correctness, i.e. termination as well as partial correctness. (This is one of various notations for total correctness.)
Examples
Example 1 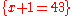

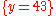
(Assignment Axiom) 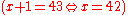
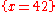


(Consequence Rule) Example 2 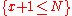
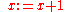
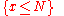
(Assignment Axiom) (  for x, N with integer types)
for x, N with integer types)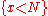
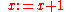

(Consequence Rule)
See also
- Communicating sequential processesCommunicating sequential processesIn computer science, Communicating Sequential Processes is a formal language for describing patterns of interaction in concurrent systems. It is a member of the family of mathematical theories of concurrency known as process algebras, or process calculi...
- Design by contractDesign by contractDesign by contract , also known as programming by contract and design-by-contract programming, is an approach to designing computer software...
- Denotational semanticsDenotational semanticsIn computer science, denotational semantics is an approach to formalizing the meanings of programming languages by constructing mathematical objects which describe the meanings of expressions from the languages...
- Dynamic logicDynamic logic (modal logic)Dynamic logic is an extension of modal logic originally intended for reasoning about computer programs and later applied to more general complex behaviors arising in linguistics, philosophy, AI, and other fields.-Language:...
- Edsger W. Dijkstra
- Loop invariantLoop invariantIn computer science, a loop invariant is an invariant used to prove properties of loops. Informally, a loop invariant is a statement of the conditions that should be true on entry into a loop and that are guaranteed to remain true on every iteration of the loop...
- Predicate transformer semanticsPredicate transformer semanticsPredicate transformer semantics was introduced by Dijkstra in his seminal paper "Guarded commands, nondeterminacy and formal derivation of programs". They define the semantics of an imperative programming paradigm by assigning to each statement in this language a corresponding predicate...
- Program verification
- Refinement calculusRefinement CalculusRefinement calculus is a formalized approach to stepwise refinement for program construction. The required behaviour of the final executable program is specified as an abstract and perhaps non-executable "program", which is then refined by a series of correctness-preserving transformations into an...
- Separation logicSeparation logicIn computer science, separation logic is an extension of Hoare logic, a way of reasoning about programs.It was developed by John C. Reynolds, Peter O'Hearn, Samin Ishtiaq and Hongseok Yang, drawing upon early work by Burstall...
- Sequent calculusSequent calculusIn proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
- Static code analysisStatic code analysisStatic program analysis is the analysis of computer software that is performed without actually executing programs built from that software In most cases the analysis is performed on some version of the source code and in the other cases some form of the object code...
Further reading
- Robert D. Tennent. Specifying Software (a textbook that includes an introduction to Hoare logic, written in 2002) ISBN 0-521-00401-2
External links
- Project Bali has defined Hoare logic-style rules for a subset of the Java programming language, for use with the Isabelle theorem proverIsabelle theorem proverThe Isabelle theorem prover is an interactive theorem prover, successor of the Higher Order Logic theorem prover. It is an LCF-style theorem prover , so it is based on a small logical core guaranteeing logical correctness...
- KeY-Hoare is a semi-automatic verification system built on top of the KeYKeYThe KeY tool is used in formal verification of Java programs.It accepts both specifications written in JML or OCL to Java source files. These are transformed into theorems of dynamic logic and then compared against program semantics which are likewise defined in terms of dynamic logic. KeY is...
theorem prover. It features a Hoare calculus for a simple while language. - j-Algo-modul Hoare calculus — A visualisation of the Hoare calculus in the algorithm visualisation program j-Algo
- Communicating sequential processes



