
Hoffman graph
Encyclopedia
In the mathematical
field of graph theory
, the Hoffman graph is a 4-regular graph
with 16 vertices and 32 edges discovered by Alan Hoffman
. Published in 1963, it is cospectral to the hypercube graph Q4.
The Hoffman graph has many common properties with the hypercube Q4—both are Hamiltonian and have chromatic number 2, chromatic index 4, radius 4, girth 4 and diameter 4. It is also a 4-vertex-connected graph
and a 4-edge-connected graph
.
and its full automorphism group is a group of order 48 isomorphic to the direct product
of the symmetric group
S4 and the cyclic group
Z/2Z.
The characteristic polynomial
of the Hoffman graph is equal to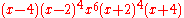
making it an integral graph
—a graph whose spectrum
consists entirely of integers. It is the same spectrum than the hypercube Q4.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Hoffman graph is a 4-regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
with 16 vertices and 32 edges discovered by Alan Hoffman
Alan Hoffman (mathematician)
Alan Jerome Hoffman, born May 30, 1924 in New York City, is a mathematician and IBM fellow emeritus, T. J. Watson Research Center, IBM, Yorktown Heights, N.Y. He is the founding editor of the Journal Linear Algebra and its Applications, and holds several patents...
. Published in 1963, it is cospectral to the hypercube graph Q4.
The Hoffman graph has many common properties with the hypercube Q4—both are Hamiltonian and have chromatic number 2, chromatic index 4, radius 4, girth 4 and diameter 4. It is also a 4-vertex-connected graph
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and a 4-edge-connected graph
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
.
Algebraic properties
The Hoffman graph is not a vertex-transitive graphVertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
and its full automorphism group is a group of order 48 isomorphic to the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S4 and the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z/2Z.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Hoffman graph is equal to
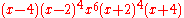
making it an integral graph
Integral graph
In the mathematical field of graph theory, an integral graph is a graph whose spectrum consists entirely of integers. In other words, a graphs is an integral graph if all the eigenvalues of its characteristic polynomial are integers....
—a graph whose spectrum
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
consists entirely of integers. It is the same spectrum than the hypercube Q4.

