Hohmann transfer orbit
Encyclopedia
In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbit
s, typically both in the same plane
.
The orbital maneuver
to perform the Hohmann transfer uses two engine impulses which move a spacecraft
onto and off the transfer orbit. This maneuver was named after Walter Hohmann
, the German
scientist who published a description of it in his 1925 book Die Erreichbarkeit der Himmelskörper (The Accessibility of Celestial Bodies). Hohmann was influenced in part by the German science fiction author Kurd Laßwitz
and his 1897 book Two Planets.
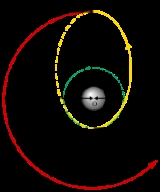
that touches both the lower circular orbit that one wishes to leave (labeled 1 on diagram) and the higher circular orbit that one wishes to reach (3 on diagram). The transfer (2 on diagram) is initiated by firing the spacecraft's engine in order to accelerate it so that it will follow the elliptical orbit; this adds energy to the spacecraft's orbit. When the spacecraft has reached its destination orbit, its orbital speed (and hence its orbital energy) must be increased again in order to change the elliptic orbit to the larger circular one.
Due to the reversibility of orbits, Hohmann transfer orbits also work to bring a spacecraft from a higher orbit into a lower one; in this case, the spacecraft's engine is fired in the opposite direction to its current path, decelerating the spacecraft and causing it to drop into the lower-energy elliptical transfer orbit. The engine is then fired again at the lower distance to decelerate the spacecraft into the lower circular orbit.
The Hohmann transfer orbit is theoretically based on two instantaneous velocity changes. Extra fuel is required to compensate for the fact that in reality the bursts take time; this is minimized by using high thrust engines to minimize the duration of the bursts. Low thrust engines can perform an approximation of a Hohmann transfer orbit, by creating a gradual enlargement of the initial circular orbit through carefully timed engine firings. This requires a change in velocity
(delta-v) that is up to 141% greater than the two impulse transfer orbit (see also below), and takes longer to complete.
and potential energy
, and this total energy also equals half the potential at the
average distance
, (the semi-major axis
):
Solving this equation for velocity results in the Vis-viva equation
,
Therefore the delta-v
required for the Hohmann transfer can be computed as follows, under the assumption of instantaneous impulses:
,
where
and 
are, respectively, the radii of the departure and arrival circular orbits;
the smaller (greater) of
and 
corresponds to the periapsis distance (apoapsis distance) of the Hohmann elliptical transfer orbit. The total 
is then:
Whether moving into a higher or lower orbit, by Kepler's third law, the time taken to transfer between the orbits is:
(one half of the orbital period
for the whole ellipse), where
is length of semi-major axis
of the Hohmann transfer orbit.
we have
= 42,164 km and e.g. 
= 6,678 km (altitude 300 km).
In the smaller circular orbit the speed is 7.73 km/s, in the larger one 3.07 km/s. In the elliptical orbit in between the speed varies from 10.15 km/s at the perigee to 1.61 km/s at the apogee.
The delta-v's are 10.15 − 7.73 = 2.42 and 3.07 − 1.61 = 1.46 km/s, together 3.88 km/s. http://www.google.com/search?num=100&hl=en&lr=&newwindow=1&safe=off&q=sqrt%28398600%2F6678%29*sqrt%282%2F%286678%2F42164%2B1%29%29
Compare with the delta-v for an escape orbit: 10.93 − 7.73 = 3.20 km/s. Applying a delta-v at the LEO
of only 0.78 km/s more (3.20-2.42) would give the rocket the escape speed, while at the geostationary orbit a delta-v of 1.46 km/s is needed for reaching the escape speed of this circular orbit. This illustrates that at large speeds the same delta-v provides more specific orbital energy
, and energy increase is maximized if one spends the delta-v as soon as possible, rather than spending some, being decelerated by gravity, and then spending some more (of course, the objective of a Hohmann transfer orbit is different).
. For higher target orbits the delta-v decreases again, and tends to 
times the original orbital speed (41.4%). The first burst tends to accelerate to the escape speed, which is 
times the circular orbit speed, and the second tends to zero.
Such a low-thrust maneuver requires more delta-v than a 2-burn Hohmann transfer maneuver, requiring more fuel for a given engine design
. However, if only low-thrust maneuvers are required on a mission, then continuously firing a very high-efficiency, low-thrust engine with a high effective exhaust velocity
might generate this higher delta-v using less total mass than a high-thrust engine using a nominally more efficient Hohmann transfer maneuver. This is more efficient for a small satellite because the additional mass of the propellant, especially for electric propulsion systems, is lower than the added mass would be for a separate high-thrust system.
to Mars
. At the beginning of its journey, the spacecraft will already have a certain velocity associated with its orbit around Earth – this is the velocity that will not need to be found when the spacecraft enters the transfer orbit (around the Sun
). At the other end, the spacecraft will need a certain velocity to orbit Mars, which will actually be less than the velocity needed to continue orbiting the Sun in the transfer orbit, let alone attempting to orbit the Sun in a Mars-like orbit. Therefore, the spacecraft will have to decelerate in order for Mars' gravity to capture it. Therefore, relatively small amounts of thrust at either end of the trip are needed to arrange the transfer. However, the alignment of the two planets in their orbits is crucial – the destination planet and the spacecraft must arrive at the same point in their respective orbits around the Sun at the same time. This requirement for alignment gives rise to the concept of launch window
s.
was published, providing even lower-energy (though much slower) paths between different orbits than Hohmann transfer orbits.
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
s, typically both in the same plane
Plane
-Physical objects:* Aeroplane or airplane, a fixed-wing aircraft* Plane , a woodworking tool to smooth surfaces* Platanus, a genus of trees with the common name "plane"* Acer pseudoplatanus, a tree species sometimes called "plane"...
.
The orbital maneuver
Orbital maneuver
In spaceflight, an orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft.For spacecraft far from Earth—for example those in orbits around the Sun—an orbital maneuver is called a deep-space maneuver .-delta-v:...
to perform the Hohmann transfer uses two engine impulses which move a spacecraft
Spacecraft
A spacecraft or spaceship is a craft or machine designed for spaceflight. Spacecraft are used for a variety of purposes, including communications, earth observation, meteorology, navigation, planetary exploration and transportation of humans and cargo....
onto and off the transfer orbit. This maneuver was named after Walter Hohmann
Walter Hohmann
Walter Hohmann was a German engineer who made an important contribution to the understanding of orbital dynamics. In a book published in 1925, Hohmann demonstrated a very fuel-efficient path to move a spacecraft between two different orbits, now called a Hohmann transfer orbit. He received his Ph.D...
, the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
scientist who published a description of it in his 1925 book Die Erreichbarkeit der Himmelskörper (The Accessibility of Celestial Bodies). Hohmann was influenced in part by the German science fiction author Kurd Laßwitz
Kurd Laßwitz
Kurd Lasswitz was a German author, scientist, and philosopher. He has been called the father of German science fiction He sometimes used the pseudonym Velatus....
and his 1897 book Two Planets.
Explanation
The diagram shows a Hohmann transfer orbit to bring a spacecraft from a lower circular orbit into a higher one. It is one half of an elliptic orbitElliptic orbit
In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
that touches both the lower circular orbit that one wishes to leave (labeled 1 on diagram) and the higher circular orbit that one wishes to reach (3 on diagram). The transfer (2 on diagram) is initiated by firing the spacecraft's engine in order to accelerate it so that it will follow the elliptical orbit; this adds energy to the spacecraft's orbit. When the spacecraft has reached its destination orbit, its orbital speed (and hence its orbital energy) must be increased again in order to change the elliptic orbit to the larger circular one.
Due to the reversibility of orbits, Hohmann transfer orbits also work to bring a spacecraft from a higher orbit into a lower one; in this case, the spacecraft's engine is fired in the opposite direction to its current path, decelerating the spacecraft and causing it to drop into the lower-energy elliptical transfer orbit. The engine is then fired again at the lower distance to decelerate the spacecraft into the lower circular orbit.
The Hohmann transfer orbit is theoretically based on two instantaneous velocity changes. Extra fuel is required to compensate for the fact that in reality the bursts take time; this is minimized by using high thrust engines to minimize the duration of the bursts. Low thrust engines can perform an approximation of a Hohmann transfer orbit, by creating a gradual enlargement of the initial circular orbit through carefully timed engine firings. This requires a change in velocity
Delta-v
In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....
(delta-v) that is up to 141% greater than the two impulse transfer orbit (see also below), and takes longer to complete.
Calculation
For a small body orbiting another, very much larger body (such as a satellite orbiting the earth), the total energy of the body is the sum of its kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
, and this total energy also equals half the potential at the
average distance
, (the semi-major axisSemi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
):
Solving this equation for velocity results in the Vis-viva equation
Vis-viva equation
In astrodynamics, the vis viva equation, also referred to as orbital energy conservation equation, is one of the fundamental and useful equations that govern the motion of orbiting bodies....
,
-
- where:
-
is the speed of an orbiting body 
is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
of the primary body and the orbiting body-
is the distance of the orbiting body from the primary focus -
is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of the body's orbit
-
Therefore the delta-v
Delta-v
In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....
required for the Hohmann transfer can be computed as follows, under the assumption of instantaneous impulses:
,where
and are, respectively, the radii of the departure and arrival circular orbits;the smaller (greater) of
and corresponds to the periapsis distance (apoapsis distance) of the Hohmann elliptical transfer orbit. The total is then:Whether moving into a higher or lower orbit, by Kepler's third law, the time taken to transfer between the orbits is:
(one half of the orbital period
Orbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
for the whole ellipse), where
is length of semi-major axisSemi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of the Hohmann transfer orbit.
Example
For the geostationary transfer orbitGeostationary transfer orbit
A geosynchronous transfer orbit or geostationary transfer orbit is a Hohmann transfer orbit used to reach geosynchronous or geostationary orbit....
we have
= 42,164 km and e.g. = 6,678 km (altitude 300 km).In the smaller circular orbit the speed is 7.73 km/s, in the larger one 3.07 km/s. In the elliptical orbit in between the speed varies from 10.15 km/s at the perigee to 1.61 km/s at the apogee.
The delta-v's are 10.15 − 7.73 = 2.42 and 3.07 − 1.61 = 1.46 km/s, together 3.88 km/s. http://www.google.com/search?num=100&hl=en&lr=&newwindow=1&safe=off&q=sqrt%28398600%2F6678%29*sqrt%282%2F%286678%2F42164%2B1%29%29
Compare with the delta-v for an escape orbit: 10.93 − 7.73 = 3.20 km/s. Applying a delta-v at the LEO
Low Earth orbit
A low Earth orbit is generally defined as an orbit within the locus extending from the Earth’s surface up to an altitude of 2,000 km...
of only 0.78 km/s more (3.20-2.42) would give the rocket the escape speed, while at the geostationary orbit a delta-v of 1.46 km/s is needed for reaching the escape speed of this circular orbit. This illustrates that at large speeds the same delta-v provides more specific orbital energy
Specific orbital energy
In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
, and energy increase is maximized if one spends the delta-v as soon as possible, rather than spending some, being decelerated by gravity, and then spending some more (of course, the objective of a Hohmann transfer orbit is different).
Worst case, maximum delta-v
A Hohmann transfer orbit from a given circular orbit to a larger circular orbit, in the case of a single central body, costs the largest delta-v (53.6% of the original orbital speed) if the radius of the target orbit is 15.6 times as large as that of the original orbit. This number is the positive root of. For higher target orbits the delta-v decreases again, and tends to times the original orbital speed (41.4%). The first burst tends to accelerate to the escape speed, which is times the circular orbit speed, and the second tends to zero.Low-thrust transfer
It can be shown that going from one circular orbit to another by gradually changing the radius costs a delta-v of simply the absolute value of the difference between the two speeds. Thus for the geostationary transfer orbit 7.73 - 3.07 = 4.66 km/s, the same as, in the absence of gravity, the deceleration would cost. In fact, acceleration is applied to compensate half of the deceleration due to moving outward. Therefore the acceleration due to thrust is equal to the deceleration due to the combined effect of thrust and gravity.Such a low-thrust maneuver requires more delta-v than a 2-burn Hohmann transfer maneuver, requiring more fuel for a given engine design
Spacecraft propulsion
Spacecraft propulsion is any method used to accelerate spacecraft and artificial satellites. There are many different methods. Each method has drawbacks and advantages, and spacecraft propulsion is an active area of research. However, most spacecraft today are propelled by forcing a gas from the...
. However, if only low-thrust maneuvers are required on a mission, then continuously firing a very high-efficiency, low-thrust engine with a high effective exhaust velocity
Specific impulse
Specific impulse is a way to describe the efficiency of rocket and jet engines. It represents the derivative of the impulse with respect to amount of propellant used, i.e., the thrust divided by the amount of propellant used per unit time. If the "amount" of propellant is given in terms of mass ,...
might generate this higher delta-v using less total mass than a high-thrust engine using a nominally more efficient Hohmann transfer maneuver. This is more efficient for a small satellite because the additional mass of the propellant, especially for electric propulsion systems, is lower than the added mass would be for a separate high-thrust system.
Application to interplanetary travel
When used to move a spacecraft from orbiting one planet to orbiting another, the situation becomes somewhat more complex. For example, consider a spacecraft travelling from the EarthEarth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
to Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
. At the beginning of its journey, the spacecraft will already have a certain velocity associated with its orbit around Earth – this is the velocity that will not need to be found when the spacecraft enters the transfer orbit (around the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
). At the other end, the spacecraft will need a certain velocity to orbit Mars, which will actually be less than the velocity needed to continue orbiting the Sun in the transfer orbit, let alone attempting to orbit the Sun in a Mars-like orbit. Therefore, the spacecraft will have to decelerate in order for Mars' gravity to capture it. Therefore, relatively small amounts of thrust at either end of the trip are needed to arrange the transfer. However, the alignment of the two planets in their orbits is crucial – the destination planet and the spacecraft must arrive at the same point in their respective orbits around the Sun at the same time. This requirement for alignment gives rise to the concept of launch window
Launch window
Launch window is a term used in spaceflight to describe a time period in which a particular launch vehicle must be launched. If the rocket does not launch within the "window", it has to wait for the next window....
s.
Interplanetary Transport Network
In 1997, a set of orbits known as the Interplanetary Transport NetworkInterplanetary Transport Network
The Interplanetary Transport Network is a collection of gravitationally determined pathways through the solar system that require very little energy for an object to follow. The ITN makes particular use of Lagrange points as locations where trajectories through space are redirected using little...
was published, providing even lower-energy (though much slower) paths between different orbits than Hohmann transfer orbits.
See also
- Delta-v budgetDelta-v budgetIn the astrodynamics and aerospace industry, a delta-v budget is the estimated delta-v requirements for the various propulsive tasks and orbital maneuvers over one or more phases of a space mission.Sample delta-v budget will enumerate various classes of maneuvers, delta-v per maneuver, number of...
- Bi-elliptic transferBi-elliptic transferIn astronautics and aerospace engineering, the bi-elliptic transfer is an orbital maneuver that moves a spacecraft from one orbit to another and may, in certain situations, require less delta-v than a Hohmann transfer....
- Geostationary transfer orbitGeostationary transfer orbitA geosynchronous transfer orbit or geostationary transfer orbit is a Hohmann transfer orbit used to reach geosynchronous or geostationary orbit....
- List of orbits
- Orbital mechanics
External links
- ORBITAL MECHANICS (Rocket and Space Technology)