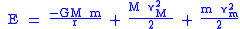Vis-viva equation
Encyclopedia
In astrodynamics
, the vis viva equation, also referred to as orbital energy conservation equation, is one of the fundamental and useful equations that govern the motion
of orbit
ing bodies.
It is the direct result of the law of conservation of energy, which requires that the sum of kinetic and potential energy be constant at all points along the orbit.
Vis viva
(Latin for "live force") is a term from the history of mechanics, and it survives in this sole context. It represents the principle that the difference between the aggregate work
of the accelerating
force
s of a system
and that of the retarding forces is equal to one half the vis viva accumulated or lost in the system while the work is being done.
(elliptic
, parabolic
, hyperbolic
or radial
), the vis viva equation is as follows:
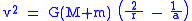
where:
The orbital energy can also be calculated using only relative quantities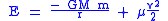
For elliptic and circular orbits, the total energy is given more concisely by
Dividing the total energy by the reduced mass gives the vis-viva energy, more commonly known in modern times as the specific orbital energy
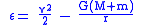
For elliptic and circular orbits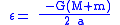
Equating the two previous expressions and solving for v yields the vis viva equation: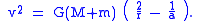
Given the total mass and the scalars r and v at a single point of the orbit, one can compute the specific orbital energy
 , allowing an object orbiting a larger object to be classified as having not enough energy to remain in orbit, hence being "suborbital" (a ballistic missile, for example), having enough energy to be "orbital", but without the possibility to complete a full orbit anyway because it eventually collides with the other body, or having enough energy to come from and/or go to infinity (as a meteor, for example).
, allowing an object orbiting a larger object to be classified as having not enough energy to remain in orbit, hence being "suborbital" (a ballistic missile, for example), having enough energy to be "orbital", but without the possibility to complete a full orbit anyway because it eventually collides with the other body, or having enough energy to come from and/or go to infinity (as a meteor, for example).
Astrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...
, the vis viva equation, also referred to as orbital energy conservation equation, is one of the fundamental and useful equations that govern the motion
Motion (physics)
In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
of orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
ing bodies.
It is the direct result of the law of conservation of energy, which requires that the sum of kinetic and potential energy be constant at all points along the orbit.
Vis viva
Vis viva
In the history of science, vis viva is an obsolete scientific theory that served as an elementary and limited early formulation of the principle of conservation of energy...
(Latin for "live force") is a term from the history of mechanics, and it survives in this sole context. It represents the principle that the difference between the aggregate work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
of the accelerating
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s of a system
System
System is a set of interacting or interdependent components forming an integrated whole....
and that of the retarding forces is equal to one half the vis viva accumulated or lost in the system while the work is being done.
Vis viva equation
For any Kepler orbitKepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
(elliptic
Elliptic orbit
In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
, parabolic
Parabolic trajectory
In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1. When moving away from the source it is called an escape orbit, otherwise a capture orbit...
, hyperbolic
Hyperbolic trajectory
In astrodynamics or celestial mechanics a hyperbolic trajectory is a Kepler orbit with the eccentricity greater than 1. Under standard assumptions a body traveling along this trajectory will coast to infinity, arriving there with hyperbolic excess velocity relative to the central body. Similarly to...
or radial
Radial trajectory
In astrodynamics and celestial mechanics a radial trajectory is a Kepler orbit with zero angular momentum. Two objects in a radial trajectory move directly towards or away from each other in a straight line.- Classification :...
), the vis viva equation is as follows:
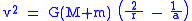
where:
 is the relative speed of the two bodies
is the relative speed of the two bodies is the distance between the two bodies
is the distance between the two bodies is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
(a>0 for ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s, or
or 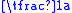 =0 for parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
=0 for parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
s, and a<0 for hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
s) is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...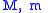 are the masses of the two bodies
are the masses of the two bodies
Derivation
The total orbital energy is the sum of the shared potential energy, the kinetic energy of body M, and the kinetic energy of body m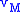 is the speed of body M relative to the inertial center of mass of the two bodies.
is the speed of body M relative to the inertial center of mass of the two bodies. is the speed of body m relative to the inertial center of mass of the two bodies.
is the speed of body m relative to the inertial center of mass of the two bodies.
The orbital energy can also be calculated using only relative quantities
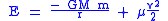
 is the relative speed of the two bodies
is the relative speed of the two bodies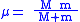 is the reduced massReduced massReduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
is the reduced massReduced massReduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
For elliptic and circular orbits, the total energy is given more concisely by

 is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
.
Dividing the total energy by the reduced mass gives the vis-viva energy, more commonly known in modern times as the specific orbital energy
Specific orbital energy
In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
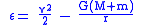
For elliptic and circular orbits
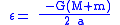
Equating the two previous expressions and solving for v yields the vis viva equation:
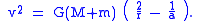
Practical applications
Given the total mass and the scalars r and v at a single point of the orbit, one can compute r and v at any other point in the orbit.Given the total mass and the scalars r and v at a single point of the orbit, one can compute the specific orbital energy
Specific orbital energy
In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
 , allowing an object orbiting a larger object to be classified as having not enough energy to remain in orbit, hence being "suborbital" (a ballistic missile, for example), having enough energy to be "orbital", but without the possibility to complete a full orbit anyway because it eventually collides with the other body, or having enough energy to come from and/or go to infinity (as a meteor, for example).
, allowing an object orbiting a larger object to be classified as having not enough energy to remain in orbit, hence being "suborbital" (a ballistic missile, for example), having enough energy to be "orbital", but without the possibility to complete a full orbit anyway because it eventually collides with the other body, or having enough energy to come from and/or go to infinity (as a meteor, for example).