Holomorph (mathematics)
Encyclopedia
In mathematics
, especially in the area of algebra
known as group theory
, the holomorph of a group
is a group which simultaneously contains (copies of) the group and its automorphism group. The holomorph provides interesting examples of groups, and allows one to treat group elements and group automorphisms in a uniform context. In group theory, for a group
, the holomorph of 
denoted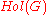 
can be described as a semidirect product
or as a permutation group
.
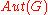is the automorphism group of 
then
where the multiplication is given by
[Eq. 1]
Typically, a semidirect product is given in the form
where 
and 
are groups and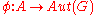 
is a homomorphism
and where the multiplication of elements in the semi-direct product is given as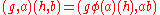
which is well defined, since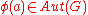
and therefore 
.
For the holomorph,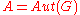
and 
is the identity map
, as such we suppress writing
explicitly in the multiplication given in [Eq. 1] above.
For example,
Observe, for example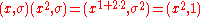
and note also that this group is not abelian
, as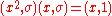
, so that 
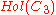is a non-abelian group of order 6 which, by basic group theory, must be isomorphic to the symmetric group
.
from G into the symmetric group
on the underlying set of G. One homomorphism is defined as λ: G → Sym(G), λ(g)(h) = g·h. That is, g is mapped to the permutation
obtained by left multiplying each element of G by g. Similarly, a second homomorphism ρ: G → Sym(G) is defined by ρ(g)(h) = h·g−1, where the inverse ensures that ρ(g·h)(k) = ρ(g)(ρ(h)(k)). These homomorphisms are called the left and right regular representation
s of G. Each homomorphism is injective, a fact referred to as Cayley's theorem
.
For example, if G = C3 = {1, x, x2 } is a cyclic group
of order three, then
so λ(x) takes (1, x, x2) to (x, x2, 1).
The image of λ is a subgroup of Sym(G) isomorphic to G, and its normalizer in Sym(G) is defined to be the holomorph H of G.
For each f in H and g in G, there is an h in G such that f·λ(g) = λ(h)·f. If an element f of the holomorph fixes the identity
of G, then for 1 in G, (f·λ(g))(1) = (λ(h)·f)(1), but the left hand side is f(g), and the right side is h. In other words, if f in H fixes the identity of G, then for every g in G, f·λ(g) = λ(f(g))·f. If g, k are elements of G, and f is an element of H fixing the identity of G, then applying this equality twice to f·λ(g)·λ(h) and once to the (equivalent) expression f·λ(g·h) gives that f(g)·f(h) = f(g·h). That is, every element of H that fixes the identity of G is in fact an automorphism
of G. Such an f normalizes any λ(g), and the only λ(g) that fixes the identity is λ(1). Setting A to be the stabilizer (group theory) of the identity, the subgroup generated by A and λ(G) is semidirect product
with normal subgroup
λ(G) and complement A. Since λ(G) is transitive, the subgroup generated by λ(G) and the point stabilizer A is all of H, which shows the holomorph as a permutation group is isomorphic to the holomorph as semidirect product.
It is useful, but not directly relevant, that the centralizer of λ(G) in Sym(G) is ρ(G), their intersection is ρ(Z(G)) = λ(Z(G)), where Z(G) is the center
of G, and that A is a common complement to both of these normal subgroups of H.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
known as group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the holomorph of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is a group which simultaneously contains (copies of) the group and its automorphism group. The holomorph provides interesting examples of groups, and allows one to treat group elements and group automorphisms in a uniform context. In group theory, for a group
, the holomorph of denoted 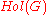can be described as a semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
or as a permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
.
Hol(G) as a semi-direct product
If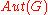 is the automorphism group of thenwhere the multiplication is given by
[Eq. 1]Typically, a semidirect product is given in the form
where and are groups and 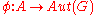is a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
and where the multiplication of elements in the semi-direct product is given as
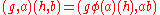
which is well defined, since
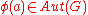and therefore .For the holomorph,
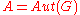and is the identity mapIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
, as such we suppress writing
explicitly in the multiplication given in [Eq. 1] above.For example,
-
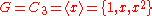the cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 3 -
where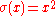 
-
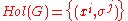with the multiplication given by -
where the exponents of 
are taken modModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
3 and those of
mod 2.
Observe, for example
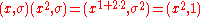
and note also that this group is not abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, as
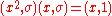, so that 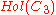is a non-abelian group of order 6 which, by basic group theory, must be isomorphic to the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.Hol(G) as a permutation group
A group G acts naturally on itself by left and right multiplication, each giving rise to a homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
from G into the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on the underlying set of G. One homomorphism is defined as λ: G → Sym(G), λ(g)(h) = g·h. That is, g is mapped to the permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
obtained by left multiplying each element of G by g. Similarly, a second homomorphism ρ: G → Sym(G) is defined by ρ(g)(h) = h·g−1, where the inverse ensures that ρ(g·h)(k) = ρ(g)(ρ(h)(k)). These homomorphisms are called the left and right regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
s of G. Each homomorphism is injective, a fact referred to as Cayley's theorem
Cayley's theorem
In group theory, Cayley's theorem, named in honor of Arthur Cayley, states that every group G is isomorphic to a subgroup of the symmetric group acting on G...
.
For example, if G = C3 = {1, x, x2 } is a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order three, then
- λ(x)(1) = x·1 = x,
- λ(x)(x) = x·x = x2, and
- λ(x)(x2) = x·x2 = 1,
so λ(x) takes (1, x, x2) to (x, x2, 1).
The image of λ is a subgroup of Sym(G) isomorphic to G, and its normalizer in Sym(G) is defined to be the holomorph H of G.
For each f in H and g in G, there is an h in G such that f·λ(g) = λ(h)·f. If an element f of the holomorph fixes the identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of G, then for 1 in G, (f·λ(g))(1) = (λ(h)·f)(1), but the left hand side is f(g), and the right side is h. In other words, if f in H fixes the identity of G, then for every g in G, f·λ(g) = λ(f(g))·f. If g, k are elements of G, and f is an element of H fixing the identity of G, then applying this equality twice to f·λ(g)·λ(h) and once to the (equivalent) expression f·λ(g·h) gives that f(g)·f(h) = f(g·h). That is, every element of H that fixes the identity of G is in fact an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of G. Such an f normalizes any λ(g), and the only λ(g) that fixes the identity is λ(1). Setting A to be the stabilizer (group theory) of the identity, the subgroup generated by A and λ(G) is semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
with normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
λ(G) and complement A. Since λ(G) is transitive, the subgroup generated by λ(G) and the point stabilizer A is all of H, which shows the holomorph as a permutation group is isomorphic to the holomorph as semidirect product.
It is useful, but not directly relevant, that the centralizer of λ(G) in Sym(G) is ρ(G), their intersection is ρ(Z(G)) = λ(Z(G)), where Z(G) is the center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of G, and that A is a common complement to both of these normal subgroups of H.