The Hopf maximum principle is a maximum principle

Maximum principle

In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...

 in the theory of second order elliptic partial differential equations and has been described as the "classic and bedrock result" of that theory. Generalizing the maximum principle for harmonic function

Harmonic function

In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....

s which was already known to Gauss in 1839, Eberhard Hopf

Eberhard Hopf

Eberhard Frederich Ferdinand Hopf was a mathematician and astronomer, one of the founding fathers of ergodic theory and a pioneer of bifurcation theory who also made significant contributions to the subjects of partial differential equations and integral equations, fluid dynamics, and differential...

 proved in 1927 that if a function satisfies a second order partial differential inequality of a certain kind in a domain of Rⁿ and attains a maximum in the domain then the function is constant. The simple idea behind Hopf's proof, the comparison technique he introduced for this purpose, has led to an enormous range of important applications and generalizations.

Mathematical formulation

Let u = u(x), x = (x₁, …, x_n) be a C² function which satisfies the differential inequality

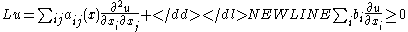
in an open domain

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 Ω, where the symmetric matrix a_ij = a_ij(x) is locally uniformly positive definite in Ω and the coefficients a_ij, b_i = b_i(x) are locally bounded. If u takes a maximum value M in Ω then u ≡ M.

It is usually thought that the Hopf maximum principle applies only to linear differential operators L. In particular, this is the point of view taken by Courant

Richard Courant

Richard Courant was a German American mathematician.- Life :Courant was born in Lublinitz in the German Empire's Prussian Province of Silesia. During his youth, his parents had to move quite often, to Glatz, Breslau, and in 1905 to Berlin. He stayed in Breslau and entered the university there...

 and Hilbert's

David Hilbert

David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...

 Methods of Mathematical Physics. In the later sections of his original paper, however, Hopf considered a more general situation which permits certain nonlinear operators L and, in some cases, leads to uniqueness statements in the Dirichlet problem

Dirichlet problem

In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....

 for the mean curvature

Mean curvature

In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....

 operator and the Monge–Ampère equation.

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.