Horseshoe lemma
Encyclopedia
In homological algebra
, the horseshoe lemma, also called the simultaneous resolution theorem, is a statement relating resolutions of two objects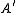
and 
to resolutions of
extensions of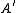
by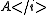 
. It says that if an object 
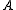is an extension of 
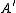by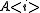 
, then a resolution of 
can be built up inductively
with the nth item in the resolution equal to the coproduct
of the nth items in the resolutions of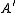
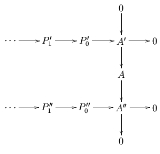
and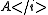 
. The name of the lemma comes from the shape of the diagram illustrating the lemma's hypothesis.
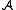be an abelian category
with enough projectives. If
is a diagram
in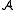
such that the column is exact
and the
rows are projective resolutions of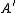
and 
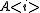respectively, then
it can be completed to a commutative diagram
where all columns are exact, the middle row is a projective resolution
of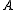
, and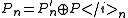 
for all n. If 
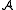is an
abelian category with enough injectives
, the dual
statement also holds.
The lemma can be proved inductively. At each stage of the induction, the properties of projective objects are used to define maps in a projective resolution of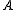
. Then the snake lemma
is invoked to show that the simultaneous resolution constructed so far has exact rows.
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, the horseshoe lemma, also called the simultaneous resolution theorem, is a statement relating resolutions of two objects
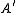and to resolutions ofextensions of
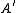by 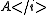. It says that if an object 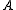is an extension of 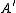by 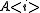, then a resolution of can be built up inductivelyMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
with the nth item in the resolution equal to the coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
of the nth items in the resolutions of
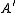and 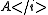. The name of the lemma comes from the shape of the diagram illustrating the lemma's hypothesis.Formal statement
Let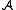 be an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
with enough projectives. If
is a diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
in
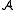such that the column is exactExact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
and the
rows are projective resolutions of
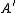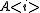and respectively, thenit can be completed to a commutative diagram
where all columns are exact, the middle row is a projective resolution
of
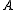, and 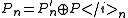for all n. If 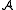is anabelian category with enough injectives
Injective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
, the dual
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
statement also holds.
The lemma can be proved inductively. At each stage of the induction, the properties of projective objects are used to define maps in a projective resolution of
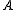. Then the snake lemmaSnake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
is invoked to show that the simultaneous resolution constructed so far has exact rows.