Snake lemma
Encyclopedia
The snake lemma is a tool used in mathematics
, particularly homological algebra
, to construct long exact sequences. The snake lemma is valid in every abelian category
and is a crucial tool in homological algebra and its applications, for instance in algebraic topology
. Homomorphisms constructed with its help are generally called connecting homomorphisms.
(such as the category of abelian group
s or the category of vector space
s over a given field), consider a commutative diagram
:
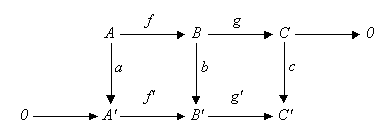
where the rows are exact sequence
s and 0 is the zero object.
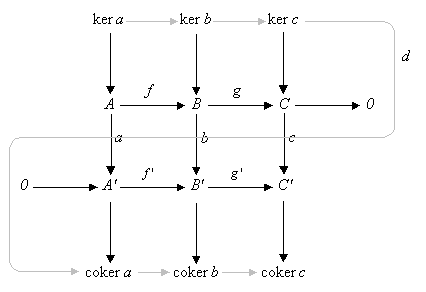
Then there is an exact sequence relating the kernels
and cokernel
s of a, b, and c:

Furthermore, if the morphism f is a monomorphism
, then so is the morphism ker a → ker b, and if g is an epimorphism
, then so is coker b → coker c.
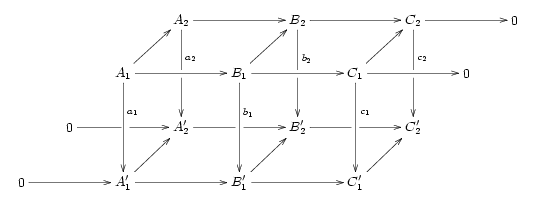
and then note that the exact sequence that is the conclusion of the lemma can be drawn on this expanded diagram in the reversed "S" shape of a slithering snake
.
In the case of abelian groups or modules
over some ring
, the map d can be constructed as follows.
Pick an element x in ker c and view it as an element of C; since g is surjective, there exists y in B with g(y) = x. Because of the commutativity of the diagram, we have g(b(y)) = c(g(y)) = c(x) = 0 (since x is in the kernel of c), and therefore b(y) is in the kernel of g' . Since the bottom row is exact, we find an element z in A' with f '(z) = b(y). z is unique by injectivity of f '. We then define d(x) = z + im(a). Now one has to check that d is well-defined (i.e. d(x) only depends on x and not on the choice of y), that it is a homomorphism, and that the resulting long sequence is indeed exact.
Once that is done, the theorem is proven for abelian groups or modules over a ring. For the general case, the argument may be rephrased in terms of properties of arrows and cancellation instead of elements. Alternatively, one may invoke Mitchell's embedding theorem
.
s). This follows from the naturality of the sequence produced by the snake lemma.
If
is a commutative diagram with exact rows, then the snake lemma can be applied twice, to the "front" and to the "back", yielding two long exact sequences; these are related by a commutative diagram of the form
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, to construct long exact sequences. The snake lemma is valid in every abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
and is a crucial tool in homological algebra and its applications, for instance in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. Homomorphisms constructed with its help are generally called connecting homomorphisms.
Statement
In an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
(such as the category of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s or the category of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over a given field), consider a commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:

where the rows are exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
s and 0 is the zero object.
Then there is an exact sequence relating the kernels
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
and cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
s of a, b, and c:

Furthermore, if the morphism f is a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, then so is the morphism ker a → ker b, and if g is an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
, then so is coker b → coker c.
Explanation of the name
To see where the snake lemma gets its name, expand the diagram above as follows:
and then note that the exact sequence that is the conclusion of the lemma can be drawn on this expanded diagram in the reversed "S" shape of a slithering snake
Snake
Snakes are elongate, legless, carnivorous reptiles of the suborder Serpentes that can be distinguished from legless lizards by their lack of eyelids and external ears. Like all squamates, snakes are ectothermic, amniote vertebrates covered in overlapping scales...
.
Construction of the maps
The maps between the kernels and the maps between the cokernels are induced in a natural manner by the given (horizontal) maps because of the diagram's commutativity. The exactness of the two induced sequences follows in a straightforward way from the exactness of the rows of the original diagram. The important statement of the lemma is that a connecting homomorphism d exists which completes the exact sequence.In the case of abelian groups or modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over some ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, the map d can be constructed as follows.
Pick an element x in ker c and view it as an element of C; since g is surjective, there exists y in B with g(y) = x. Because of the commutativity of the diagram, we have g(b(y)) = c(g(y)) = c(x) = 0 (since x is in the kernel of c), and therefore b(y) is in the kernel of g' . Since the bottom row is exact, we find an element z in A' with f '(z) = b(y). z is unique by injectivity of f '. We then define d(x) = z + im(a). Now one has to check that d is well-defined (i.e. d(x) only depends on x and not on the choice of y), that it is a homomorphism, and that the resulting long sequence is indeed exact.
Once that is done, the theorem is proven for abelian groups or modules over a ring. For the general case, the argument may be rephrased in terms of properties of arrows and cancellation instead of elements. Alternatively, one may invoke Mitchell's embedding theorem
Mitchell's embedding theorem
Mitchell's embedding theorem, also known as the Freyd–Mitchell theorem, is a result stating that every abelian category admits a full and exact embedding into the category of R-modules...
.
Naturality
In the applications, one often needs to show that long exact sequences are "natural" (in the sense of natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s). This follows from the naturality of the sequence produced by the snake lemma.
If
is a commutative diagram with exact rows, then the snake lemma can be applied twice, to the "front" and to the "back", yielding two long exact sequences; these are related by a commutative diagram of the form
In popular culture
- The proof of the snake lemma is being taught by Jill ClayburghJill ClayburghJill Clayburgh was an American actress. She received Academy Award nominations for her roles in An Unmarried Woman and Starting Over.-Personal life:...
at the very beginning of the 1980 film It's My TurnIt's My Turn (film)It's My Turn is a 1980 romantic comedy-drama film starring Jill Clayburgh, Michael Douglas, and Charles Grodin.The film was directed by Claudia Weill and written by Eleanor Bergstein...
.
External links
- Snake Lemma at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...