Hurst exponent
Encyclopedia
The Hurst exponent is used as a measure of the long term memory
of time series
. It relates to the autocorrelation
s of the time series and the rate at which these decrease as the lag between pairs of values increases.
Studies involving the Hurst exponent were originally developed in hydrology
for the practical matter of determining optimum dam sizing for the Nile river's volatile rain and drought conditions that had been observed over a long period of time. The name "Hurst exponent" or Hurst coefficient derives from Harold Edwin Hurst
(1880–1978), who was the lead researcher in these studies, and the use of the standard notation H for the coefficent relates to this name also.
In fractal geometry, the generalized Hurst exponent, has been denoted by H
or Hq in honor of both Harold Edwin Hurst
(1880–1978) and Ludwig Otto Hölder (1859–1937) by Benoît Mandelbrot
(1924-2010).
The Hurst exponent is referred to as the "index of dependence", or "index of long-range dependence". It quantifies the relative tendency of a time series
either to regress strongly to the mean or to cluster in a direction. A value H in the range 0.5 < H < 1 indicates a time series with long-term positive autocorrelation, meaning both that a high value in the series will probably be followed by another high value and that the values a long time into the future will also tend to be high. A value in the range 0 < H < 0.5 indicates a time series with long-term switching between high and low values in adjacent pairs, meaning that a single high value will probably be followed by a low value and that the value after that will tend to be high, with this tendency to switch between high and low values lasting a long time into the future. A value of H=0.5 can indicate a completely uncorrelated series, but in fact it is the value applicable to series for which the autocorrelations at small time lags can be positive or negative but where the absolute values of the autocorrelations decay exponentially quickly to zero. This in contrast to the typically power law
decay for the 0.5 < H < 1 and 0 < H < 0.5 cases.
as a function of the time span of a time series as follows;
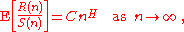
where;
on the time span n of observation. A time series of full length N is divided into a number of shorter time series of length n = N, N/2, N/4, ... The average rescaled range is then calculated for each value of n.
For a (partial) time series of length
, 
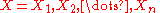, the rescaled range is calculated as follows:
1. Calculate the mean
;
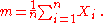
2. Create a mean-adjusted series;
3. Calculate the cumulative deviate series
;
4. Compute the range
;
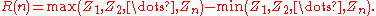
5. Compute the standard deviation
;
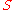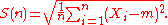
6. Calculate the rescaled range
and average over all the partial time series of length 
The Hurst exponent is estimated by fitting the power law
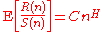to the data.
There are a variety of techniques that exist for estimating H, however assessing the accuracy of the estimation can be a complicated issue. Mathematically, in one technique, the Hurst exponent can be estimated such that:
for a time series
may be defined by the scaling properties of its structure
functions Sq(
):
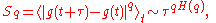
where q > 0,
is the time lag and averaging is over the time window
usually the largest time scale of the system.
Practically, in nature, there is no limit to time, and thus H is non-deterministic as it may only be estimated based on the observed data; e.g., the most dramatic daily move upwards ever seen in a stock market index can always be exceeded during some subsequent day.
H is directly related to fractal dimension
, D, such that D = 2 - H. The values of the Hurst exponent vary between 0 and 1, with higher values indicating a smoother trend, less volatility, and less roughness.
In the above mathematical estimation technique, the function H(q) contains information about averaged generalized volatilities at scale
(only q = 1, 2 are used to define the volatility). In particular, the H1 exponent indicates persistent (H1 > ½) or antipersistent (H1 < ½) behavior of the trend.
For the BRW (brown noise, 1/f²) one gets
while for the pink noise
(1/f) and white noise
we have
For the popular Levy stable processes and truncated Levy processes with parameter α it has been found that
A method to estimate
from non-stationary time series is called detrended fluctuation analysis
.
When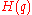
is a non-linear function of q the time series is a multifractal system
.
of the stochastic process then yields variance scaling, but is not needed for long time memory. E.g., both Markov process
es (i.e., memory-free processes) and fractional Brownian motion scale at the level of 1-point densities (simple averages), but neither scales at the level of pair correlations or, correspondingly, the 2-point probability density.
An efficient market requires a martingale condition, and unless the variance is linear in the time this produces nonstationary increments, x(t+T)-x(t)≠x(T)-x(0). Martingales are Markovian at the level of pair correlations, meaning that pair correlations cannot be used to beat a martingale market. Stationary increments with nonlinear variance, on the other hand, induce the long time pair memory of fractional Brownian motion that would make the market beatable at the level of pair correlations. Such a market would necessarily be far from "efficient".
Long-range dependency
Long-range dependency is a phenomenon that may arise in the analysis of spatial or time series data. It relates to the rate of decay of statistical dependence, with the implication that this decays more slowly than an exponential decay, typically a power-like decay...
of time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
. It relates to the autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
s of the time series and the rate at which these decrease as the lag between pairs of values increases.
Studies involving the Hurst exponent were originally developed in hydrology
Hydrology
Hydrology is the study of the movement, distribution, and quality of water on Earth and other planets, including the hydrologic cycle, water resources and environmental watershed sustainability...
for the practical matter of determining optimum dam sizing for the Nile river's volatile rain and drought conditions that had been observed over a long period of time. The name "Hurst exponent" or Hurst coefficient derives from Harold Edwin Hurst
Harold Edwin Hurst
Harold Edwin Hurst was a British hydrologist. Hurst's study on measuring the long-term storage capacity of reservoirs documented the presence of long-range dependence in hydrology. Much of Hurst's research was motivated by his empirical observations of the Nile. The Hurst exponent, which has been...
(1880–1978), who was the lead researcher in these studies, and the use of the standard notation H for the coefficent relates to this name also.
In fractal geometry, the generalized Hurst exponent, has been denoted by H
H (disambiguation)
H is the eighth letter of the Latin alphabet.H may also refer to:- Musical symbols :* H number, Harry Halbreich reference mechanism for music by Honegger and Martinů* H, B * H, B major- People :* H...
or Hq in honor of both Harold Edwin Hurst
Harold Edwin Hurst
Harold Edwin Hurst was a British hydrologist. Hurst's study on measuring the long-term storage capacity of reservoirs documented the presence of long-range dependence in hydrology. Much of Hurst's research was motivated by his empirical observations of the Nile. The Hurst exponent, which has been...
(1880–1978) and Ludwig Otto Hölder (1859–1937) by Benoît Mandelbrot
Benoît Mandelbrot
Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
(1924-2010).
The Hurst exponent is referred to as the "index of dependence", or "index of long-range dependence". It quantifies the relative tendency of a time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
either to regress strongly to the mean or to cluster in a direction. A value H in the range 0.5 < H < 1 indicates a time series with long-term positive autocorrelation, meaning both that a high value in the series will probably be followed by another high value and that the values a long time into the future will also tend to be high. A value in the range 0 < H < 0.5 indicates a time series with long-term switching between high and low values in adjacent pairs, meaning that a single high value will probably be followed by a low value and that the value after that will tend to be high, with this tendency to switch between high and low values lasting a long time into the future. A value of H=0.5 can indicate a completely uncorrelated series, but in fact it is the value applicable to series for which the autocorrelations at small time lags can be positive or negative but where the absolute values of the autocorrelations decay exponentially quickly to zero. This in contrast to the typically power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
decay for the 0.5 < H < 1 and 0 < H < 0.5 cases.
Definition
The Hurst exponent, H, is defined in terms of the asymptotic behaviour of the rescaled rangeRescaled range
The rescaled range is a statistical measure of the variability of a time series introduced by the British hydrologist Harold Edwin Hurst...
as a function of the time span of a time series as follows;
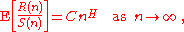
where;
-
is the rescaled rangeRescaled rangeThe rescaled range is a statistical measure of the variability of a time series introduced by the British hydrologist Harold Edwin Hurst...
-
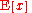is the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
- n is the time span of the observation (number of data points in a time series)
- C is a constant.
Estimating the exponent
To estimate the Hurst exponent, one must first estimate the dependence of the rescaled rangeRescaled range
The rescaled range is a statistical measure of the variability of a time series introduced by the British hydrologist Harold Edwin Hurst...
on the time span n of observation. A time series of full length N is divided into a number of shorter time series of length n = N, N/2, N/4, ... The average rescaled range is then calculated for each value of n.
For a (partial) time series of length
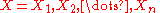, , the rescaled range is calculated as follows:1. Calculate the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
;
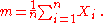
2. Create a mean-adjusted series;
3. Calculate the cumulative deviate series
;4. Compute the range
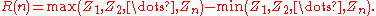
;5. Compute the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
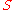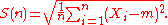
;6. Calculate the rescaled range
and average over all the partial time series of length The Hurst exponent is estimated by fitting the power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
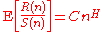to the data.Generalized exponent
The basic Hurst exponent can be related to the expected size of changes, as a function of the lag between observations, as measured by E(|Xt+τ-Xt|2). For the generalized form of the coefficient, the exponent here is replaced by a more general term, denoted by q.There are a variety of techniques that exist for estimating H, however assessing the accuracy of the estimation can be a complicated issue. Mathematically, in one technique, the Hurst exponent can be estimated such that:
- Hq = H(q),
for a time series
- g(t) (t = 1, 2,...)
may be defined by the scaling properties of its structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
functions Sq(
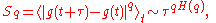
):where q > 0,
is the time lag and averaging is over the time windowusually the largest time scale of the system.
Practically, in nature, there is no limit to time, and thus H is non-deterministic as it may only be estimated based on the observed data; e.g., the most dramatic daily move upwards ever seen in a stock market index can always be exceeded during some subsequent day.
H is directly related to fractal dimension
Fractal dimension
In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
, D, such that D = 2 - H. The values of the Hurst exponent vary between 0 and 1, with higher values indicating a smoother trend, less volatility, and less roughness.
In the above mathematical estimation technique, the function H(q) contains information about averaged generalized volatilities at scale
(only q = 1, 2 are used to define the volatility). In particular, the H1 exponent indicates persistent (H1 > ½) or antipersistent (H1 < ½) behavior of the trend.For the BRW (brown noise, 1/f²) one gets
- Hq = ½,
while for the pink noise
Pink noise
Pink noise or 1/ƒ noise is a signal or process with a frequency spectrum such that the power spectral density is inversely proportional to the frequency. In pink noise, each octave carries an equal amount of noise power...
(1/f) and white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
we have
- Hq = 0.
For the popular Levy stable processes and truncated Levy processes with parameter α it has been found that
- Hq = q/α for q < α and Hq = 1 for q ≥ α.
A method to estimate
from non-stationary time series is called detrended fluctuation analysisDetrended fluctuation analysis
In stochastic processes, chaos theory and time series analysis, detrended fluctuation analysis is a method for determining the statistical self-affinity of a signal. It is useful for analysing time series that appear to be long-memory processes In stochastic processes, chaos theory and time series...
.
When
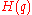is a non-linear function of q the time series is a multifractal systemMultifractal system
A multifractal system is a generalization of a fractal system in which a single exponent is not enough to describe its dynamics; instead, a continuous spectrum of exponents is needed....
.
Note
In the above definition two separate requirements are mixed together as if they would be one. Here are the two independent requirements: (i) stationarity of the increments, x(t+T)-x(t)=x(T)-x(0) in distribution. this is the condition that yields long time autocorrelations. (ii) Self-similaritySelf-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...
of the stochastic process then yields variance scaling, but is not needed for long time memory. E.g., both Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
es (i.e., memory-free processes) and fractional Brownian motion scale at the level of 1-point densities (simple averages), but neither scales at the level of pair correlations or, correspondingly, the 2-point probability density.
An efficient market requires a martingale condition, and unless the variance is linear in the time this produces nonstationary increments, x(t+T)-x(t)≠x(T)-x(0). Martingales are Markovian at the level of pair correlations, meaning that pair correlations cannot be used to beat a martingale market. Stationary increments with nonlinear variance, on the other hand, induce the long time pair memory of fractional Brownian motion that would make the market beatable at the level of pair correlations. Such a market would necessarily be far from "efficient".
External links
- http://www.scientio.com/Products/ChaosKit Scientio's ChaosKit product calculates hurst exponents amongst other Chaotic measures. Access is provided online via a web service and Graphic user interface.
- http://www.trusoft-international.com TruSoft's Benoit - Fractal Analysis Software product calculates hurst exponents and fractal dimensions.