
Detrended fluctuation analysis
Encyclopedia
In stochastic processes, chaos theory and time series analysis, detrended fluctuation analysis (DFA) is a method for determining the statistical self-affinity
of a signal. It is useful for analysing time series that appear to be long-memory processes (diverging correlation time, e.g. power-law decaying autocorrelation function) or 1/f noise.
The obtained exponent is similar to the Hurst exponent
, except that DFA may also be applied to signals whose underlying statistics (such as mean and variance) or dynamics are non-stationary
(changing with time). It is related to measures based upon spectral techniques such as autocorrelation
and Fourier transform
.
DFA was introduced by Peng et al. 1994 and represents an extension of the (ordinary) fluctuation analysis (FA), which is affected by non-stationarities.
 ,
,  , integration or summation first converts this into an unbounded process
, integration or summation first converts this into an unbounded process 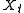 :
:

 is called cumulative sum or profile. This process converts, for example, an i.i.d. white noise
is called cumulative sum or profile. This process converts, for example, an i.i.d. white noise
process into a random walk
.
Next, is divided into time windows
is divided into time windows  of length
of length  samples, and a local least squares
samples, and a local least squares
straight-line fit (the local trend) is calculated by minimising the squared error with respect to the slope and intercept parameters
with respect to the slope and intercept parameters  :
:
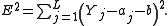
Trends of higher order, can be removed by higher order DFA, where the linear function is replaced by a polynomial of order
is replaced by a polynomial of order  .
.
Next, the root-mean-square deviation from the trend, the fluctuation, is calculated over every window at every time scale:

This detrending followed by fluctuation measurement process is repeated over the whole signal at a range of different window sizes , and a log-log graph
, and a log-log graph
of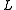 against
against  is constructed.
is constructed.
A straight line on this log-log graph indicates statistical self-affinity
expressed as . The scaling exponent
. The scaling exponent  is calculated as the slope of a straight line fit to the log-log graph of
is calculated as the slope of a straight line fit to the log-log graph of  against
against  using least-squares. This exponent is a generalization of the Hurst exponent
using least-squares. This exponent is a generalization of the Hurst exponent
. Because the expected displacement in an uncorrelated random walk of length L grows like , an exponent of
, an exponent of  would correspond to uncorrelated white noise. When the exponent is between 0 and 1, the result is Fractional Brownian motion, with the precise value giving information about the series self-correlations:
would correspond to uncorrelated white noise. When the exponent is between 0 and 1, the result is Fractional Brownian motion, with the precise value giving information about the series self-correlations:
There are different orders of DFA. In the described case, linear fits ( ) are applied to the profile, thus it is called DFA1. In general, DFA
) are applied to the profile, thus it is called DFA1. In general, DFA , uses polynomial fits of order
, uses polynomial fits of order  . Due to the summation (integration) from
. Due to the summation (integration) from  to
to  , linear trends in the mean of the profile represent constant trends in the initial sequence, and DFA1 only removes such constant trends (steps) in the
, linear trends in the mean of the profile represent constant trends in the initial sequence, and DFA1 only removes such constant trends (steps) in the  . In general DFA of order
. In general DFA of order  removes (polynomial) trends of order
removes (polynomial) trends of order  . For linear trends in the mean of
. For linear trends in the mean of 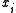 at least DFA2 is needed. The Hurst R/S analysis
at least DFA2 is needed. The Hurst R/S analysis
removes constants trends in the original sequence and thus, in its detrending it is equivalent to DFA1.
The DFA method was applied to many systems, ranging from DNA sequences and speech pathology detection to heartbeat fluctuation different sleep stages . Effect of trends on DFA were studied in and relation to the power spectrum method is presented in .
Since in the fluctuation function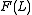 the square(root) is used, DFA measures the scaling-behavior of the second moment-fluctuations, this means
the square(root) is used, DFA measures the scaling-behavior of the second moment-fluctuations, this means  . The multifractal generalization (MF-DFA) uses a variable moment
. The multifractal generalization (MF-DFA) uses a variable moment 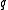 and provides
and provides 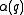 . Kantelhardt et al. intended this scaling exponent as a generalization of the classical Hurst exponent. The classical Hurst exponent corresponds to the second moment for stationary cases
. Kantelhardt et al. intended this scaling exponent as a generalization of the classical Hurst exponent. The classical Hurst exponent corresponds to the second moment for stationary cases  and to the second moment minus 1 for nonstationary cases
and to the second moment minus 1 for nonstationary cases 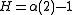 .
.
decays with an exponent :
:
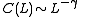 .
.
In addition the power spectrum decays as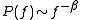 .
.
The three exponent are related by:
The relations can be derived using the Wiener–Khinchin theorem
.
Thus, is tied to the slope of the power spectrum
is tied to the slope of the power spectrum  used to describe the color of noise by this relationship:
used to describe the color of noise by this relationship:  .
.
For fractional Gaussian noise (FGN), we have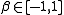 , and thus
, and thus  , and
, and  , where
, where  is the Hurst exponent
is the Hurst exponent
. for FGN is equal to
for FGN is equal to 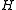 .
.
For fractional Brownian motion (FBM), we have , and thus
, and thus  , and
, and  , where
, where  is the Hurst exponent
is the Hurst exponent
. for FBM is equal to
for FBM is equal to  . In this context, FBM is the cumulative sum or the integral
. In this context, FBM is the cumulative sum or the integral
of FGN, thus, the exponents of their
power spectra differ by 2.
 by the DFA method, but this does not necessarily imply that the time series is self-similar. Self-similarity requires that the points on the log-log graph are sufficiently collinear across a very wide range of window sizes
by the DFA method, but this does not necessarily imply that the time series is self-similar. Self-similarity requires that the points on the log-log graph are sufficiently collinear across a very wide range of window sizes  .
.
Also, there are many scaling exponent-like quantities that can be measured for a self-similar time series, including the divider dimension and Hurst exponent
. Therefore, the DFA scaling exponent is not a fractal dimension
is not a fractal dimension
sharing all the desirable properties of the Hausdorff dimension
, for example, although in certain special cases it can be shown to be related to the box-counting dimension for the graph of a time series.
Self-affinity
In mathematics, self-affinity refers to a fractal whose pieces are scaled by different amounts in the x- and y-directions. We refer to these as being the 2-dimensional axes, like that of a grid. This means that in order to appreciate the self similarity of these fractal objects, they have to be...
of a signal. It is useful for analysing time series that appear to be long-memory processes (diverging correlation time, e.g. power-law decaying autocorrelation function) or 1/f noise.
The obtained exponent is similar to the Hurst exponent
Hurst exponent
The Hurst exponent is used as a measure of the long term memory of time series. It relates to the autocorrelations of the time series and the rate at which these decrease as the lag between pairs of values increases....
, except that DFA may also be applied to signals whose underlying statistics (such as mean and variance) or dynamics are non-stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
(changing with time). It is related to measures based upon spectral techniques such as autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
and Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.
DFA was introduced by Peng et al. 1994 and represents an extension of the (ordinary) fluctuation analysis (FA), which is affected by non-stationarities.
Calculation
Given a bounded time seriesTime series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
 ,
,  , integration or summation first converts this into an unbounded process
, integration or summation first converts this into an unbounded process 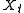 :
:
 is called cumulative sum or profile. This process converts, for example, an i.i.d. white noise
is called cumulative sum or profile. This process converts, for example, an i.i.d. white noiseWhite noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
process into a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
.
Next,
 is divided into time windows
is divided into time windows  of length
of length  samples, and a local least squares
samples, and a local least squaresLeast squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
straight-line fit (the local trend) is calculated by minimising the squared error
 with respect to the slope and intercept parameters
with respect to the slope and intercept parameters  :
: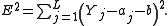
Trends of higher order, can be removed by higher order DFA, where the linear function
 is replaced by a polynomial of order
is replaced by a polynomial of order  .
.Next, the root-mean-square deviation from the trend, the fluctuation, is calculated over every window at every time scale:

This detrending followed by fluctuation measurement process is repeated over the whole signal at a range of different window sizes
 , and a log-log graph
, and a log-log graphLog-log graph
In science and engineering, a log-log graph or log-log plot is a two-dimensional graph of numerical data that uses logarithmic scales on both the horizontal and vertical axes...
of
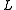 against
against  is constructed.
is constructed.A straight line on this log-log graph indicates statistical self-affinity
Self-affinity
In mathematics, self-affinity refers to a fractal whose pieces are scaled by different amounts in the x- and y-directions. We refer to these as being the 2-dimensional axes, like that of a grid. This means that in order to appreciate the self similarity of these fractal objects, they have to be...
expressed as
 . The scaling exponent
. The scaling exponent  is calculated as the slope of a straight line fit to the log-log graph of
is calculated as the slope of a straight line fit to the log-log graph of  against
against  using least-squares. This exponent is a generalization of the Hurst exponent
using least-squares. This exponent is a generalization of the Hurst exponentHurst exponent
The Hurst exponent is used as a measure of the long term memory of time series. It relates to the autocorrelations of the time series and the rate at which these decrease as the lag between pairs of values increases....
. Because the expected displacement in an uncorrelated random walk of length L grows like
 , an exponent of
, an exponent of  would correspond to uncorrelated white noise. When the exponent is between 0 and 1, the result is Fractional Brownian motion, with the precise value giving information about the series self-correlations:
would correspond to uncorrelated white noise. When the exponent is between 0 and 1, the result is Fractional Brownian motion, with the precise value giving information about the series self-correlations:-
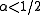 : anti-correlated
: anti-correlated -
 : uncorrelated, white noiseWhite noiseWhite noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
: uncorrelated, white noiseWhite noiseWhite noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency... -
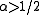 : correlated
: correlated -
 : 1/f-noise, pink noisePink noisePink noise or 1/ƒ noise is a signal or process with a frequency spectrum such that the power spectral density is inversely proportional to the frequency. In pink noise, each octave carries an equal amount of noise power...
: 1/f-noise, pink noisePink noisePink noise or 1/ƒ noise is a signal or process with a frequency spectrum such that the power spectral density is inversely proportional to the frequency. In pink noise, each octave carries an equal amount of noise power... -
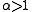 : non-stationary, random walk like, unbounded
: non-stationary, random walk like, unbounded -
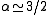 : Brownian noiseBrownian noiseIn science, Brownian noise , also known as Brown noise or red noise, is the kind of signal noise produced by Brownian motion, hence its alternative name of random walk noise...
: Brownian noiseBrownian noiseIn science, Brownian noise , also known as Brown noise or red noise, is the kind of signal noise produced by Brownian motion, hence its alternative name of random walk noise...
There are different orders of DFA. In the described case, linear fits (
 ) are applied to the profile, thus it is called DFA1. In general, DFA
) are applied to the profile, thus it is called DFA1. In general, DFA , uses polynomial fits of order
, uses polynomial fits of order  . Due to the summation (integration) from
. Due to the summation (integration) from  to
to  , linear trends in the mean of the profile represent constant trends in the initial sequence, and DFA1 only removes such constant trends (steps) in the
, linear trends in the mean of the profile represent constant trends in the initial sequence, and DFA1 only removes such constant trends (steps) in the  . In general DFA of order
. In general DFA of order  removes (polynomial) trends of order
removes (polynomial) trends of order  . For linear trends in the mean of
. For linear trends in the mean of 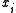 at least DFA2 is needed. The Hurst R/S analysis
at least DFA2 is needed. The Hurst R/S analysisRescaled range
The rescaled range is a statistical measure of the variability of a time series introduced by the British hydrologist Harold Edwin Hurst...
removes constants trends in the original sequence and thus, in its detrending it is equivalent to DFA1.
The DFA method was applied to many systems, ranging from DNA sequences and speech pathology detection to heartbeat fluctuation different sleep stages . Effect of trends on DFA were studied in and relation to the power spectrum method is presented in .
Since in the fluctuation function
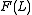 the square(root) is used, DFA measures the scaling-behavior of the second moment-fluctuations, this means
the square(root) is used, DFA measures the scaling-behavior of the second moment-fluctuations, this means  . The multifractal generalization (MF-DFA) uses a variable moment
. The multifractal generalization (MF-DFA) uses a variable moment 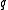 and provides
and provides 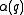 . Kantelhardt et al. intended this scaling exponent as a generalization of the classical Hurst exponent. The classical Hurst exponent corresponds to the second moment for stationary cases
. Kantelhardt et al. intended this scaling exponent as a generalization of the classical Hurst exponent. The classical Hurst exponent corresponds to the second moment for stationary cases  and to the second moment minus 1 for nonstationary cases
and to the second moment minus 1 for nonstationary cases 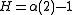 .
.Relations to other methods
In the case of power-law decaying auto-correlations, the correlation functionCorrelation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
decays with an exponent
 :
: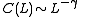 .
.In addition the power spectrum decays as
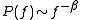 .
.The three exponent are related by:
-
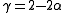
-
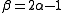 and
and -
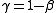 .
.
The relations can be derived using the Wiener–Khinchin theorem
Wiener–Khinchin theorem
The Wiener–Khinchin theorem states that the power spectral density of a wide–sense stationary random process is the Fourier transform of the corresponding autocorrelation function.-History:Norbert Wiener first published the result in...
.
Thus,
 is tied to the slope of the power spectrum
is tied to the slope of the power spectrum  used to describe the color of noise by this relationship:
used to describe the color of noise by this relationship:  .
.For fractional Gaussian noise (FGN), we have
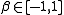 , and thus
, and thus  , and
, and  , where
, where  is the Hurst exponent
is the Hurst exponentHurst exponent
The Hurst exponent is used as a measure of the long term memory of time series. It relates to the autocorrelations of the time series and the rate at which these decrease as the lag between pairs of values increases....
.
 for FGN is equal to
for FGN is equal to 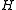 .
.For fractional Brownian motion (FBM), we have
 , and thus
, and thus  , and
, and  , where
, where  is the Hurst exponent
is the Hurst exponentHurst exponent
The Hurst exponent is used as a measure of the long term memory of time series. It relates to the autocorrelations of the time series and the rate at which these decrease as the lag between pairs of values increases....
.
 for FBM is equal to
for FBM is equal to  . In this context, FBM is the cumulative sum or the integral
. In this context, FBM is the cumulative sum or the integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of FGN, thus, the exponents of their
power spectra differ by 2.
Pitfalls in interpretation
As with most methods that depend upon line fitting, it is always possible to find a number by the DFA method, but this does not necessarily imply that the time series is self-similar. Self-similarity requires that the points on the log-log graph are sufficiently collinear across a very wide range of window sizes
by the DFA method, but this does not necessarily imply that the time series is self-similar. Self-similarity requires that the points on the log-log graph are sufficiently collinear across a very wide range of window sizes  .
.Also, there are many scaling exponent-like quantities that can be measured for a self-similar time series, including the divider dimension and Hurst exponent
Hurst exponent
The Hurst exponent is used as a measure of the long term memory of time series. It relates to the autocorrelations of the time series and the rate at which these decrease as the lag between pairs of values increases....
. Therefore, the DFA scaling exponent
 is not a fractal dimension
is not a fractal dimensionFractal dimension
In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
sharing all the desirable properties of the Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
, for example, although in certain special cases it can be shown to be related to the box-counting dimension for the graph of a time series.
Related topics
- Random walks
- Long range correlations
- Self affinitySelf-affinityIn mathematics, self-affinity refers to a fractal whose pieces are scaled by different amounts in the x- and y-directions. We refer to these as being the 2-dimensional axes, like that of a grid. This means that in order to appreciate the self similarity of these fractal objects, they have to be...
- time series analysis
- Hurst exponentHurst exponentThe Hurst exponent is used as a measure of the long term memory of time series. It relates to the autocorrelations of the time series and the rate at which these decrease as the lag between pairs of values increases....
- Fluctuations analysis
- Long term persistence
External links
- Tutorial on how to calculate detrended fluctuation analysis in Matlab using the Neurophysiological Biomarker Toolbox.
- FastDFA MATLABMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
code for rapidly calculating the DFA scaling exponent on very large datasets. - Physionet A good overview of DFA and C code to calculate it.

