Wiener–Khinchin theorem
Encyclopedia
The Wiener–Khinchin theorem (also known as the Wiener–Khintchine theorem and sometimes as the Wiener–Khinchin–Einstein theorem or the Khinchin–Kolmogorov theorem) states that the power spectral density
of a wide–sense stationary random process is the Fourier transform
of the corresponding autocorrelation
function.
first published the result in 1930, Khinchin independently later in 1934. Einstein had anticipated the idea in a brief two-page memo in 1914.
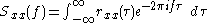
where
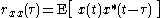
is the autocorrelation function (also called autocovariance
) defined in terms of statistical expectation
, and where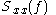
is the power spectral density of the function 
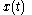. Note that the autocorrelation function is defined in terms of the expected value of a product, and that the Fourier transform of 
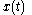does not exist in general, because stationary random functions are not square integrable
.
The asterisk denotes complex conjugate, and can be omitted if the random process is real-valued.
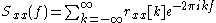
where
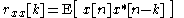
and where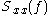
is the power spectral density of the function with discrete values 
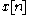. Being a sampled and discrete-time sequence, the spectral density is periodic in the frequency domain.
, LTI systems, when the inputs and outputs are not square integrable, so their Fourier transforms do not exist. A corollary is that the Fourier transform of the autocorrelation function of the output of an LTI system is equal to the product of the Fourier transform of the autocorrelation function of the input of the system times the squared magnitude of the Fourier transform of the system impulse response.
This works even when the Fourier transforms of the input and output signals do not exist because these signals are not square integrable, so the system inputs and outputs cannot be directly related by the Fourier transform of the impulse response.
Since the Fourier transform of the autocorrelation function of a signal is the power spectrum of the signal, this corollary is equivalent to saying that the power spectrum of the output is equal to the power spectrum of the input times the power transfer function
.
This corollary is used in the parametric method for power spectrum estimation.
and autocorrelation
, the Wiener–Khinchin theorem is a simple Fourier transform pair, trivially provable for any square integrable function, i.e. for functions whose Fourier transforms exist. More usefully, and historically, the theorem applies to wide-sense-stationary random processes
, signals whose Fourier transforms do not exist, using the definition of autocorrelation function in terms of expected value rather than an infinite integral. This trivialization of the Wiener–Khinchin theorem is commonplace in modern technical literature, and obscures the contributions of Aleksandr Yakovlevich Khinchin
, Norbert Wiener
, and Andrey Kolmogorov
.
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
of a wide–sense stationary random process is the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the corresponding autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
function.
History
Norbert WienerNorbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
first published the result in 1930, Khinchin independently later in 1934. Einstein had anticipated the idea in a brief two-page memo in 1914.
Continuous case
For the continuous case: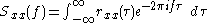where
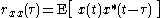
is the autocorrelation function (also called autocovariance
Autocovariance
In statistics, given a real stochastic process X, the autocovariance is the covariance of the variable with itself, i.e. the variance of the variable against a time-shifted version of itself...
) defined in terms of statistical expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, and where
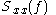is the power spectral density of the function 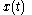. Note that the autocorrelation function is defined in terms of the expected value of a product, and that the Fourier transform of 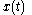does not exist in general, because stationary random functions are not square integrableSquare-integrable function
In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite...
.
The asterisk denotes complex conjugate, and can be omitted if the random process is real-valued.
Discrete case
For the discrete case: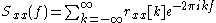where
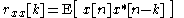
and where
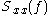is the power spectral density of the function with discrete values 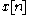. Being a sampled and discrete-time sequence, the spectral density is periodic in the frequency domain.Application
The theorem is useful for analyzing linear time-invariant systemsLTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
, LTI systems, when the inputs and outputs are not square integrable, so their Fourier transforms do not exist. A corollary is that the Fourier transform of the autocorrelation function of the output of an LTI system is equal to the product of the Fourier transform of the autocorrelation function of the input of the system times the squared magnitude of the Fourier transform of the system impulse response.
This works even when the Fourier transforms of the input and output signals do not exist because these signals are not square integrable, so the system inputs and outputs cannot be directly related by the Fourier transform of the impulse response.
Since the Fourier transform of the autocorrelation function of a signal is the power spectrum of the signal, this corollary is equivalent to saying that the power spectrum of the output is equal to the power spectrum of the input times the power transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
.
This corollary is used in the parametric method for power spectrum estimation.
Discrepancy of definition
By the definitions involving infinite integrals in the articles on spectral densitySpectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
and autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
, the Wiener–Khinchin theorem is a simple Fourier transform pair, trivially provable for any square integrable function, i.e. for functions whose Fourier transforms exist. More usefully, and historically, the theorem applies to wide-sense-stationary random processes
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
, signals whose Fourier transforms do not exist, using the definition of autocorrelation function in terms of expected value rather than an infinite integral. This trivialization of the Wiener–Khinchin theorem is commonplace in modern technical literature, and obscures the contributions of Aleksandr Yakovlevich Khinchin
Aleksandr Yakovlevich Khinchin
Aleksandr Yakovlevich Khinchin was a Soviet mathematician and one of the most significant people in the Soviet school of probability theory. He was born in the village of Kondrovo, Kaluga Governorate, Russian Empire. While studying at Moscow State University, he became one of the first followers...
, Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
, and Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
.