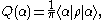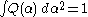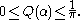Husimi Q representation
Encyclopedia
The Husimi-Q distribution is a mathematical tool used in physics, and was introduced in 1940. The Q-representation is a quasi-probability distribution commonly used in quantum mechanics
and also to represent the quantum state of light
. It is used in the field of quantum optics
and particularly for tomographic
purposes. It is also applied in the study of quantum
effects in superconductors.
) is the simplest distribution of quasi-probability in phase space
. It is defined as
which is
times the probability
distribution for the state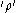
to be found in the coherent state
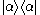. It produces a pictorial representation of the state 
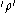to illustrate several of its mathematical properties. Essentially,
it is a convolution by a phase-space Gaussian distribution of the Wigner quasi-probability distribution
.
The Q-distribution is normalized to unity,
and is non-negative definite and bounded:
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and also to represent the quantum state of light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
. It is used in the field of quantum optics
Quantum optics
Quantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
and particularly for tomographic
Tomography
Tomography refers to imaging by sections or sectioning, through the use of any kind of penetrating wave. A device used in tomography is called a tomograph, while the image produced is a tomogram. The method is used in radiology, archaeology, biology, geophysics, oceanography, materials science,...
purposes. It is also applied in the study of quantum
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
effects in superconductors.
Definition and properties
The Husimi-Q distribution (called Q-function in the context of quantum opticsQuantum optics
Quantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
) is the simplest distribution of quasi-probability in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. It is defined as
which is
times the probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
distribution for the state
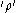to be found in the coherent stateCoherent state
In quantum mechanics a coherent state is a specific kind of quantum state of the quantum harmonic oscillator whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator...
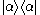. It produces a pictorial representation of the state 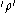to illustrate several of its mathematical properties. Essentially,it is a convolution by a phase-space Gaussian distribution of the Wigner quasi-probability distribution
Wigner quasi-probability distribution
The Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
.
The Q-distribution is normalized to unity,
and is non-negative definite and bounded:
See also
- Nonclassical lightNonclassical lightNonclassical light is any state of light that cannot be described using classical electromagnetism; its characteristics are described by the quantised electromagnetic field and quantum mechanics...
- Wigner quasi-probability distributionWigner quasi-probability distributionThe Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
- Glauber–Sudarshan P-representation