Hutchinson metric
Encyclopedia
.png)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hutchinson metric is a function which measures
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
"the discrepancy between two image
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
s for use in fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
" and "can also be applied to describe the similarity between DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
sequences expressed as real or complex genomic signals."
Formal definition
Consider only nonempty, compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, and finite metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. For a space
, let 
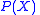denote the space of Borel probability measures on 
, with
the embedding associating to
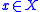the point measure 
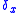. The support 
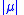of a measure in P(X) is the smallest closed subset of measure 1.If
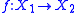
is Borel measurable then the induced map
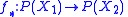
associates to
the measure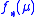 
defined by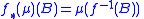
for all
Borel in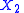 
.Then the Hutchinson metric is given by
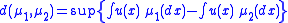
where the
is taken over all real-valued functions u with Lipschitz constant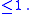
Then
is an isometric embedding of 
into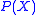 
, and if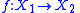
is Lipschitz then
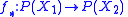
is Lipschitz with the same Lipschitz constant.
See also
- Acoustic metricAcoustic metricIn mathematical physics, a metric describes the arrangement of relative distances within a surface or volume, usually measured by signals passing through the region – essentially describing the intrinsic geometry of the region. An acoustic metric will describe the signal-carrying properties...
- Apophysis (software)
- Complete metric
- Fractal image compressionFractal compressionFractal compression is a lossy compression method for digital images, based on fractals. The method is best suited for textures and natural images, relying on the fact that parts of an image often resemble other parts of the same image...
- Image differencingImage differencingImage differencing is an image processing technique used to determine changes between images. The difference between two images is calculated by finding the difference between each pixel in each image, and generating an image based on the result...
- Metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
- Multifractal systemMultifractal systemA multifractal system is a generalization of a fractal system in which a single exponent is not enough to describe its dynamics; instead, a continuous spectrum of exponents is needed....