
Hyperhomology
Encyclopedia
In homological algebra
, the hyperhomology or hypercohomology of a complex
of objects of an abelian category
is an extension of the usual homology of an object to complexes.
It is a sort of cross between the derived functor cohomology of an object and the homology of a chain complex.
Hyperhomology is no longer used much: since about 1970 it has been largely replaced by the roughly equivalent concept of a derived functor
between derived categories.
Suppose that A is an abelian category with enough injectives and F a left exact functor to another abelian category B.
If C is a complex of objects of A bounded on the left, the hypercohomology
of C (for an integer i) is
calculated as follows:
The hypercohomology of C is independent of the choice of the quasi-isomorphism
, up to unique isomorphisms.
The hypercohomology can also be defined using derived categories
: the hypercohomology of C is just the cohomology of F(C) considered as an element of the derived category of B.
s; one with E2 term
and the other with E1 term
and E2 term
both converging to the hypercohomology
where RjF is a right derived functor of F.
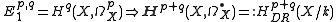
turns out to be a quasi-isomorphism and induces an isomorphism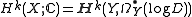 .
.
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, the hyperhomology or hypercohomology of a complex
of objects of an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
is an extension of the usual homology of an object to complexes.
It is a sort of cross between the derived functor cohomology of an object and the homology of a chain complex.
Hyperhomology is no longer used much: since about 1970 it has been largely replaced by the roughly equivalent concept of a derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
between derived categories.
Definition
We give the definition for hypercohomology as this is more common. As usual, hypercohomology and hyperhomology are essentially the same: one converts from one to the other by changing the direction of all arrows, replacing injective objects with projective ones, and so on.Suppose that A is an abelian category with enough injectives and F a left exact functor to another abelian category B.
If C is a complex of objects of A bounded on the left, the hypercohomology
- Hi(C)
of C (for an integer i) is
calculated as follows:
- Take a quasi-isomorphismQuasi-isomorphismIn homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
Φ : C → I, here I is a complex of injective elements of A. - The hypercohomology Hi(C) of C is then the cohomology Hi(F(I)) of the complex F(I).
The hypercohomology of C is independent of the choice of the quasi-isomorphism
Quasi-isomorphism
In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
, up to unique isomorphisms.
The hypercohomology can also be defined using derived categories
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
: the hypercohomology of C is just the cohomology of F(C) considered as an element of the derived category of B.
The hypercohomology spectral sequences
There are two hypercohomology spectral sequenceSpectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
s; one with E2 term
- Hi(RjF(C))
and the other with E1 term
- RjF(Ci)
and E2 term
- RjF(Hi(C))
both converging to the hypercohomology
- Hi+j(C),
where RjF is a right derived functor of F.
Examples
- For a variety X over a field k, the second spectral sequence from above gives the Hodge to de Rham spectral sequence for algebraic de Rham cohomology:
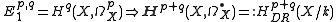
- Another example comes from the holomorphic log complexLogarithmic formIn contexts including complex manifolds and algebraic geometry, a logarithmic differential form is a meromorphic differential form with poles of a certain kind....
on a complex manifold. Let X be a complex algebraic manifold and a good compactification. This means that Y is a compact algebraic manifold and
a good compactification. This means that Y is a compact algebraic manifold and 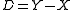 is a divisor on
is a divisor on 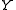 with simple normal crossings. The natural inclusion of complexes of sheaves
with simple normal crossings. The natural inclusion of complexes of sheaves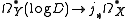
turns out to be a quasi-isomorphism and induces an isomorphism
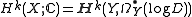 .
.

