Logarithmic form
Encyclopedia
In contexts including complex manifold
s and algebraic geometry
, a logarithmic differential form
is a meromorphic differential form with pole
s of a certain kind.
Let X be a complex manifold, and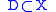
a divisor
and
a holomorphic p-form on 
. If 
and 
have a pole of order at most one along D, then 
is said to have a logarithmic pole along D. 
is also known as a logarithmic p-form. The logarithmic p-forms make up a subsheaf
of the meromorphic p-forms on X with a pole along D, denoted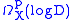
.
In the theory of Riemann surfaces, one encounters logarithmic one-forms which have the local expression
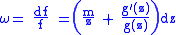
for some meromorphic function
(resp. rational function
)
, where g is holomorphic and non-vanishing at 0, and m is the order of f at 0.. That is, for some open covering, there are local representations of this differential form as a logarithmic derivative
(modified slightly with the exterior derivative
d in place of the usual differential operator
d/dz). Observe that
has only simple poles with integer residues. On higher dimensional complex manifolds, the Poincaré residue
is used to describe the distinctive behavior of logarithmic forms along poles.
and the fact that exterior differentiation d satisfies 
, one has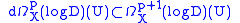
.
This implies that there is a complex of sheaves
, known as the holomorphic log complex corresponding to the divisor D. This is a subcomplex of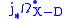 
, where 
is the inclusion and 
is the complex of sheaves of holomorphic forms on 
.
Of special interest is the case where D has simple normal crossings
. Then if
are the smooth, irreducible components of 
, one has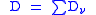 
with the 
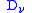meeting transversely. Locally 
is the union of hyperplanes, with local defining equations of the form 
in some holomorphic coordinates. One can show that the stalk of 
at p satisfies
and that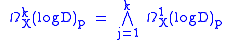
.
Some authors, e.g. , use the term log complex to refer to the holomorphic log complex corresponding to a divisor with normal crossings.
satisfying 
, where 
and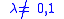 
is a complex number. Then D is a smooth irreducible hypersurface
in
and, in particular, a divisor with simple normal crossings. There is a meromorphic two-form on 
which has a simple pole along D. The Poincaré residue of
along D is given by the holomorphic one-form
.
Vital to the residue theory of logarithmic forms is the Gysin sequence
, which is in some sense a generalization of the Residue Theorem
for compact Riemann surfaces. This can be used to show, for example, that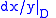
extends to a holomorphic one-form on the projective closure of D in 
, a smooth elliptic curve.
of complex algebraic varieties. Let X be a complex algebraic manifold and
a good compactification. This means that Y is a compact algebraic manifold and 
is a divisor on 
with simple normal crossings. The natural inclusion of complexes of sheaves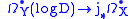
turns out to be a quasi-isomorphism. Thus
where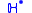
denotes hypercohomology of a complex of abelian sheaves. There is a decreasing filtration 
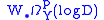given by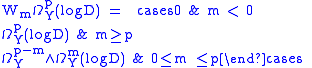
which, along with the trivial increasing filtration
on logarithmic p-forms, produces filtrations on cohomology
.
One shows that
can actually be defined over 
. Then the filtrations 
on cohomology give rise to a mixed Hodge structure on 
.
Classically, for example in elliptic function
theory, the logarithmic differential forms were recognised as complementary to the differentials of the first kind. They were sometimes called differentials of the second kind (and, with an unfortunate inconsistency, also sometimes of the third kind). The classical theory has now been subsumed as an aspect of Hodge theory. For a Riemann surface S, for example, the differentials of the first kind account for the term H1,0 in H1(S), when by the Dolbeault isomorphism it is interpreted as the sheaf cohomology
group H0(S,Ω); this is tautologous considering their definition. The H1,0 direct summand in H1(S), as well as being interpreted as H1(S,O) where O is the sheaf of holomorphic function
s on S, can be identified more concretely with a vector space of logarithmic differentials.
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a logarithmic differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
is a meromorphic differential form with pole
Pole
-General:*Poles, people originating from inbitating or inhabiting the country of Poland*Pole -Fictional:*Jill Pole, a fictional character from C. S...
s of a certain kind.
Let X be a complex manifold, and
a divisorDivisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
and
a holomorphic p-form on . If and have a pole of order at most one along D, then is said to have a logarithmic pole along D. is also known as a logarithmic p-form. The logarithmic p-forms make up a subsheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of the meromorphic p-forms on X with a pole along D, denoted
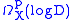.In the theory of Riemann surfaces, one encounters logarithmic one-forms which have the local expression
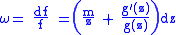
for some meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
(resp. rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
)
, where g is holomorphic and non-vanishing at 0, and m is the order of f at 0.. That is, for some open covering, there are local representations of this differential form as a logarithmic derivativeLogarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
(modified slightly with the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
d in place of the usual differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
d/dz). Observe that
has only simple poles with integer residues. On higher dimensional complex manifolds, the Poincaré residuePoincaré residue
In mathematics, the Poincaré residue is a generalization, to several complex variables and complex manifold theory, of the residue at a pole of complex function theory. It is just one of a number of such possible extensions....
is used to describe the distinctive behavior of logarithmic forms along poles.
Holomorphic Log Complex
By definition of and the fact that exterior differentiation d satisfies , one has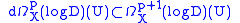.This implies that there is a complex of sheaves
, known as the holomorphic log complex corresponding to the divisor D. This is a subcomplex of 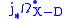, where is the inclusion and is the complex of sheaves of holomorphic forms on .Of special interest is the case where D has simple normal crossings
Normal crossings
In algebraic geometry normal crossings is the property of intersecting geometric objects to do it in a transversal way.-Normal crossing divisors:...
. Then if
are the smooth, irreducible components of , one has 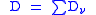with the 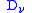meeting transversely. Locally is the union of hyperplanes, with local defining equations of the form in some holomorphic coordinates. One can show that the stalk of at p satisfiesand that
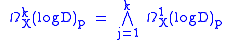.Some authors, e.g. , use the term log complex to refer to the holomorphic log complex corresponding to a divisor with normal crossings.
Higher Dimensional Example
Consider a once-punctured elliptic curve, given as the locus D of complex points satisfying , where and 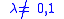is a complex number. Then D is a smooth irreducible hypersurfaceHypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
in
and, in particular, a divisor with simple normal crossings. There is a meromorphic two-form on which has a simple pole along D. The Poincaré residue of
along D is given by the holomorphic one-form.Vital to the residue theory of logarithmic forms is the Gysin sequence
Gysin sequence
In the field of mathematics known as algebraic topology, the Gysin sequence is a long exact sequence which relates the cohomology classes of the base space, the fiber and the total space of a sphere bundle. The Gysin sequence is a useful tool for calculating the cohomology rings given the Euler...
, which is in some sense a generalization of the Residue Theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
for compact Riemann surfaces. This can be used to show, for example, that
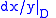extends to a holomorphic one-form on the projective closure of D in , a smooth elliptic curve.Hodge Theory
The holomorphic log complex can be brought to bear on the Hodge theoryHodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
of complex algebraic varieties. Let X be a complex algebraic manifold and
a good compactification. This means that Y is a compact algebraic manifold and is a divisor on with simple normal crossings. The natural inclusion of complexes of sheaves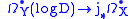turns out to be a quasi-isomorphism. Thus
where
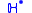denotes hypercohomology of a complex of abelian sheaves. There is a decreasing filtration 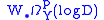given by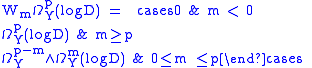which, along with the trivial increasing filtration
on logarithmic p-forms, produces filtrations on cohomology.One shows that
can actually be defined over . Then the filtrations on cohomology give rise to a mixed Hodge structure on .Classically, for example in elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
theory, the logarithmic differential forms were recognised as complementary to the differentials of the first kind. They were sometimes called differentials of the second kind (and, with an unfortunate inconsistency, also sometimes of the third kind). The classical theory has now been subsumed as an aspect of Hodge theory. For a Riemann surface S, for example, the differentials of the first kind account for the term H1,0 in H1(S), when by the Dolbeault isomorphism it is interpreted as the sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
group H0(S,Ω); this is tautologous considering their definition. The H1,0 direct summand in H1(S), as well as being interpreted as H1(S,O) where O is the sheaf of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s on S, can be identified more concretely with a vector space of logarithmic differentials.
External links
See Also
- Algebraic GeometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
- Adjunction formula
- Differential of the first kindDifferential of the first kindIn mathematics, differential of the first kind is a traditional term used in the theories of Riemann surfaces and algebraic curves , for everywhere-regular differential 1-forms...
- Residue TheoremResidue theoremThe residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...