
Normal crossings
Encyclopedia
In algebraic geometry
normal crossings is the property of intersecting geometric objects to do it in a transversal way.
, normal crossing divisors are a class of divisors
which generalize the smooth divisors. Intuitively they cross only in a transversal way.
Let A be an algebraic variety
, and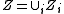 a reduced Cartier divisor
a reduced Cartier divisor
, with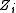 its irreducible components. Then Z is called a smooth normal crossing divisor if either
its irreducible components. Then Z is called a smooth normal crossing divisor if either
A is a curve
, or all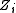 are smooth, and for each component
are smooth, and for each component 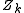 ,
, 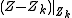 is a smooth normal crossing divisor.
is a smooth normal crossing divisor.
Equivalently, one says that a reduced divisor has normal crossings if each point étale locally
looks like the intersection of coordinate hyperplanes.
a normal crossings singularity is a point in an algebraic variety
that is locally isomorphic to a normal crossings divisor.
a simple normal crossings singularity is a point in an algebraic variety
, the latter having smooth
irreducible components
, that is locally isomorphic to a normal crossings divisor.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
normal crossings is the property of intersecting geometric objects to do it in a transversal way.
Normal crossing divisors
In algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, normal crossing divisors are a class of divisors
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
which generalize the smooth divisors. Intuitively they cross only in a transversal way.
Let A be an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, and
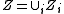 a reduced Cartier divisor
a reduced Cartier divisorDivisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
, with
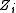 its irreducible components. Then Z is called a smooth normal crossing divisor if either
its irreducible components. Then Z is called a smooth normal crossing divisor if eitherA is a curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
, or all
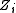 are smooth, and for each component
are smooth, and for each component 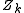 ,
, 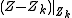 is a smooth normal crossing divisor.
is a smooth normal crossing divisor.Equivalently, one says that a reduced divisor has normal crossings if each point étale locally
Étale topology
In algebraic geometry, the étale topology is a Grothendieck topology on the category of schemes which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic...
looks like the intersection of coordinate hyperplanes.
Normal crossings singularity
In algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
a normal crossings singularity is a point in an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
that is locally isomorphic to a normal crossings divisor.
Simple normal crossings singularity
In algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
a simple normal crossings singularity is a point in an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, the latter having smooth
Smooth
Smooth means having a texture that lacks friction. Not rough.Smooth may also refer to:-In mathematics:* Smooth function, a function that is infinitely differentiable; used in calculus and topology...
irreducible components
Irreducible component
In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
, that is locally isomorphic to a normal crossings divisor.
Examples
- The normal crossing points in the algebraic variety called the Whitney umbrellaWhitney umbrellaright|frame|240px|Section of the surfaceIn mathematics, the Whitney umbrella is a self-intersecting surface placed in three dimensions...
are not simple normal crossings singularities. - The origin in the algebraic variety defined by
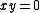 is a simple normal crossings singularity. The variety itself, seen as a subvariety of the two-dimensional affine planeCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is a simple normal crossings singularity. The variety itself, seen as a subvariety of the two-dimensional affine planeCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is an example of a normal crossings divisor.

