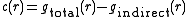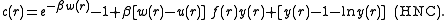Hypernetted-chain equation
Encyclopedia
In statistical mechanics
the hypernetted-chain equation is a closure
relation to solve the Ornstein–Zernike equation
which relates the direct correlation function to the total correlation function. It is commonly used in fluid theory to obtain e.g. expressions for the radial distribution function
. It is given by:
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
the hypernetted-chain equation is a closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
relation to solve the Ornstein–Zernike equation
Ornstein–Zernike equation
In statistical mechanics the Ornstein–Zernike equation is an integral equation for defining the direct correlation function. It basically describes how the correlation between two molecules can be calculated...
which relates the direct correlation function to the total correlation function. It is commonly used in fluid theory to obtain e.g. expressions for the radial distribution function
Radial distribution function
In statistical mechanics, a radial distribution function , g, describes how the atomic density varies as a function of the distance from one particular atom....
. It is given by:
-
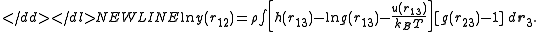
Derivation
The direct correlation function represents the direct correlation between two particles in a system containing N − 2 other particles. It can be represented by
where
is the radial distribution functionRadial distribution functionIn statistical mechanics, a radial distribution function , g, describes how the atomic density varies as a function of the distance from one particular atom....
, i.e.
(with w(r) the potential of mean forcePotential of mean forceThe Potential of Mean Force of a system with N molecules is strictly the potential that gives the average force over all the configurations of all the n+1...N molecules acting on a particle at any fixed configuration keeping fixed a set of molecules 1...n...
) and
is the radial distribution function without the direct interaction between pairs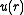 
included; i.e. we write 
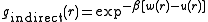. Thus we approximate c(r) by
By expanding the indirect part of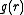
in the above equation and introducing the function 
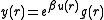we can approximate 
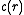by writing:
This equation is the essence of the hypernetted chain equation for if we substitute this result in the Ornstein–Zernike equationOrnstein–Zernike equationIn statistical mechanics the Ornstein–Zernike equation is an integral equation for defining the direct correlation function. It basically describes how the correlation between two molecules can be calculated...
, one obtains the hypernetted-chain equation:
-
See also
- Classical-map hypernetted-chain method
- Percus–Yevick approximationPercus–Yevick approximationIn statistical mechanics the Percus–Yevick approximation is a closure relation to solve the Ornstein–Zernike equation. It is also referred to as the Percus–Yevick equation. It is commonly used in fluid theory to obtain e.g...
– another closure relation
-
