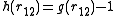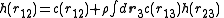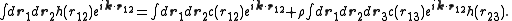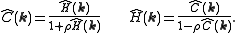Ornstein–Zernike equation
Encyclopedia
In statistical mechanics
the Ornstein–Zernike equation (named after Leonard Salomon Ornstein and Frits Zernike
) is an integral equation
for defining the direct correlation function
. It basically describes how the correlation
between two molecules can be calculated. Its applications can mainly be found in fluid theory.
It is convenient to define the total correlation function:
which is a measure for the "influence" of molecule 1 on molecule 2 at a distance
away with 
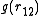as the radial distribution function
. In 1914 Ornstein and Zernike proposed to split this influence into two contributions, a direct and indirect part. The direct contribution is defined to be given by the direct correlation function, denoted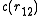
. The indirect part is due to the influence of molecule 1 on a third molecule, labeled 3, which in turn affects molecule 2, directly and indirectly. This indirect effect is weighted by the density and averaged over all the possible positions of particle 3. This decomposition can be written down mathematically as
which is called the Ornstein–Zernike equation. The OZ equation has the interesting property that if one multiplies the equation by
with 
and integrate with respect to 
and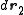 
one obtains:
If we then denote the Fourier transforms of h(r) and c(r) by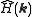
and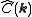 
this rearranges to
from which we obtain that
In order to solve this equation a closure
relation must be found. One commonly used closure relation is the Percus–Yevick approximation
.
More information can be found in.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
the Ornstein–Zernike equation (named after Leonard Salomon Ornstein and Frits Zernike
Frits Zernike
Frits Zernike was a Dutch physicist and winner of the Nobel prize for physics in 1953 for his invention of the phase contrast microscope, an instrument that permits the study of internal cell structure without the need to stain and thus kill the cells....
) is an integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
for defining the direct correlation function
Correlation function (statistical mechanics)
In statistical mechanics, the correlation function is a measure of the order in a system, as characterized by a mathematical correlation function, and describes how microscopic variables at different positions are correlated....
. It basically describes how the correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
between two molecules can be calculated. Its applications can mainly be found in fluid theory.
Derivation
The derivation below is heuristic in nature: rigorous derivations require extensive graph analysis or functional techniques. The interested reader is referred to for the full derivation.It is convenient to define the total correlation function:
which is a measure for the "influence" of molecule 1 on molecule 2 at a distance
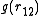away with as the radial distribution functionRadial distribution function
In statistical mechanics, a radial distribution function , g, describes how the atomic density varies as a function of the distance from one particular atom....
. In 1914 Ornstein and Zernike proposed to split this influence into two contributions, a direct and indirect part. The direct contribution is defined to be given by the direct correlation function, denoted
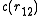. The indirect part is due to the influence of molecule 1 on a third molecule, labeled 3, which in turn affects molecule 2, directly and indirectly. This indirect effect is weighted by the density and averaged over all the possible positions of particle 3. This decomposition can be written down mathematically as
which is called the Ornstein–Zernike equation. The OZ equation has the interesting property that if one multiplies the equation by
with and integrate with respect to and 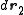one obtains:
If we then denote the Fourier transforms of h(r) and c(r) by
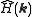and 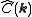this rearranges to
from which we obtain that
In order to solve this equation a closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
relation must be found. One commonly used closure relation is the Percus–Yevick approximation
Percus–Yevick approximation
In statistical mechanics the Percus–Yevick approximation is a closure relation to solve the Ornstein–Zernike equation. It is also referred to as the Percus–Yevick equation. It is commonly used in fluid theory to obtain e.g...
.
More information can be found in.
See also
- Percus–Yevick approximationPercus–Yevick approximationIn statistical mechanics the Percus–Yevick approximation is a closure relation to solve the Ornstein–Zernike equation. It is also referred to as the Percus–Yevick equation. It is commonly used in fluid theory to obtain e.g...
, a closure relation for solving the OZ equation - Hypernetted-chain equationHypernetted-chain equationIn statistical mechanics the hypernetted-chain equation is a closure relation to solve the Ornstein–Zernike equation which relates the direct correlation function to the total correlation function. It is commonly used in fluid theory to obtain e.g. expressions for the radial distribution function...
, a closure relation for solving the OZ equation
External links
- The Ornstein–Zernike equation and integral equations
- Multilevel wavelet solver for the Ornstein–Zernike equation Abstract
- Analytical solution of the Ornstein–Zernike equation for a multicomponent fluid
- The Ornstein–Zernike equation in the canonical ensemble
- Ornstein–Zernike Theory for Finite-Range Ising Models Above Tc
- OzOS, (a Linux distributionLinux distributionA Linux distribution is a member of the family of Unix-like operating systems built on top of the Linux kernel. Such distributions are operating systems including a large collection of software applications such as word processors, spreadsheets, media players, and database applications...
named after Leonard Salomon Ornstein and Frederik ZernikeFrits ZernikeFrits Zernike was a Dutch physicist and winner of the Nobel prize for physics in 1953 for his invention of the phase contrast microscope, an instrument that permits the study of internal cell structure without the need to stain and thus kill the cells....
)