Hörmander's condition
Encyclopedia
In mathematics
, Hörmander's condition is a property of vector field
s that, if satisfied, has many useful consequences in the theory of partial
and stochastic differential equation
s. The condition is named after the Swedish
mathematician
Lars Hörmander
.
V and W on d-dimension
al Euclidean space
Rd, let [V, W] denote their Lie bracket
, another vector field defined by
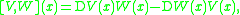
where DV(x) denotes the Fréchet derivative
of V at x ∈ Rd, which can be thought of as a matrix
that is applied to the vector W(x), and vice versa.
Let A0, A1, ... An be vector fields on Rd. They are said to satisfy Hörmander's condition if, for every point x ∈ Rd, the vectors
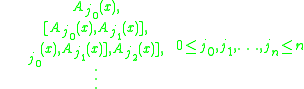
span
Rd. They are said to satisfy the parabolic Hörmander condition if the same holds true, but with the index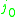
taking only values in 1,...,n.
F by
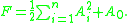
An important problem in the theory of partial differential equations is to determine sufficient conditions on the vector fields Ai for the Cauchy problem
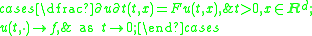
has a smooth fundamental solution
, i.e. a real-valued function p (0, +∞) × R2d→R such that p(t, ·, ·) is smooth on R2d for each t and
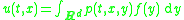
satisfies the Cauchy problem above. It had been known for some time that a smooth solution exists in the elliptic
case, in which
and the matrix A = (aji), 1 ≤ j ≤ d, 1 ≤ i ≤ n is such that AA∗ is everywhere an invertible matrix.
The great achievement of Hörmander's 1967 paper was to show that a smooth fundamental solution exists under a considerably weaker assumption: the parabolic version of the condition that now bears his name.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Hörmander's condition is a property of vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s that, if satisfied, has many useful consequences in the theory of partial
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
and stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
s. The condition is named after the Swedish
Sweden
Sweden , officially the Kingdom of Sweden , is a Nordic country on the Scandinavian Peninsula in Northern Europe. Sweden borders with Norway and Finland and is connected to Denmark by a bridge-tunnel across the Öresund....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Lars Hörmander
Lars Hörmander
Lars Valter Hörmander is a Swedish mathematician who has been called "the foremost contributor to the modern theory of linear partial differential equations". He was awarded the Fields Medal in 1962, and the Wolf Prize in 1988...
.
Definition
Given two C1 vector fieldsSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
V and W on d-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd, let [V, W] denote their Lie bracket
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
, another vector field defined by
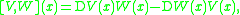
where DV(x) denotes the Fréchet derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
of V at x ∈ Rd, which can be thought of as a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that is applied to the vector W(x), and vice versa.
Let A0, A1, ... An be vector fields on Rd. They are said to satisfy Hörmander's condition if, for every point x ∈ Rd, the vectors
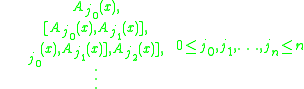
span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
Rd. They are said to satisfy the parabolic Hörmander condition if the same holds true, but with the index
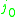taking only values in 1,...,n.Application to the Cauchy problem
With the same notation as above, define a second-order differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
F by
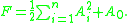
An important problem in the theory of partial differential equations is to determine sufficient conditions on the vector fields Ai for the Cauchy problem
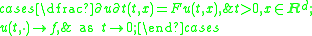
has a smooth fundamental solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
, i.e. a real-valued function p (0, +∞) × R2d→R such that p(t, ·, ·) is smooth on R2d for each t and
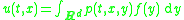
satisfies the Cauchy problem above. It had been known for some time that a smooth solution exists in the elliptic
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
case, in which
and the matrix A = (aji), 1 ≤ j ≤ d, 1 ≤ i ≤ n is such that AA∗ is everywhere an invertible matrix.
The great achievement of Hörmander's 1967 paper was to show that a smooth fundamental solution exists under a considerably weaker assumption: the parabolic version of the condition that now bears his name.