Ideal quotient
Encyclopedia
In abstract algebra
, if I and J are ideals
of a commutative ring
R, their ideal quotient (I : J) is the set
.
Then (I : J) is itself an ideal in R. The ideal quotient is viewed as a quotient because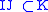
if and only if 
. The ideal quotient is useful for calculating primary decompositions. It also arises in the description of the set difference in algebraic geometry
.
Because of the notation, (I : J) is sometimes referred to as a colon ideal. There is an unrelated notion of the inverse of an ideal, known as a fractional ideal
which is defined for Dedekind rings.
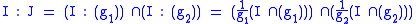
Then elimination theory can be used to calculate the intersection of I with (g1) and (g2):
Calculate a Gröbner basis
for tI + (1-t)(g1) with respect to lexicographic order. Then the basis functions which have no t in them generate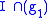
.
. More precisely,
where I denotes the taking of the ideal associated to a subset.
where "cl" denotes the Zariski
closure
, and Z denotes the taking of the variety defined by the ideal I.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, if I and J are ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of a commutative ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R, their ideal quotient (I : J) is the set
.Then (I : J) is itself an ideal in R. The ideal quotient is viewed as a quotient because
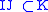if and only if . The ideal quotient is useful for calculating primary decompositions. It also arises in the description of the set difference in algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
Because of the notation, (I : J) is sometimes referred to as a colon ideal. There is an unrelated notion of the inverse of an ideal, known as a fractional ideal
Fractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
which is defined for Dedekind rings.
Properties
The ideal quotient satisfies the following properties:-
-
-
-
-
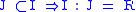
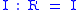
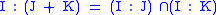
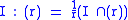(as long as R is an integral domain)
Calculating the quotient
The above properties can be used to calculate the quotient of ideals in a polynomial ring given their generators. For example, if I = (f1, f2, f3) and J = (g1, g2) are ideals in k[x1, ..., xn], then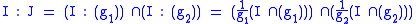Then elimination theory can be used to calculate the intersection of I with (g1) and (g2):
Calculate a Gröbner basis
Gröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
for tI + (1-t)(g1) with respect to lexicographic order. Then the basis functions which have no t in them generate
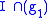.Geometric interpretation
The ideal quotient corresponds to set difference in algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. More precisely,
- If W is an affine variety and V is a subset of the affine space (not necessarily a variety), then
- I(V) : I(W) = I(V \ W),
where I denotes the taking of the ideal associated to a subset.
- If I and J are ideals in k[x1, ..., xn], then
- Z(I : J) = cl(Z(I) \ Z(J)),
where "cl" denotes the Zariski
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
, and Z denotes the taking of the variety defined by the ideal I.