
Iitaka dimension
Encyclopedia
In algebraic geometry
, the Iitaka dimension of a line bundle
L on an algebraic variety X is the dimension of the image of the rational map to projective space
determined by L. This is 1 less than the dimension of the ring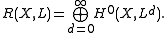
The Iitaka dimension of L is always less than or equal to the dimension of X. If L is not effective, then its Iitaka dimension is defined to be (or sometimes −1).
(or sometimes −1).
All ample line bundles are big.
Big line bundles need not determine birational isomorphisms of X with its image. For example, if C is a curve of genus 2, then the canonical bundle KC is big, but it determines a two-to-one covering, a morphism C to its image as canonical curve, which here is a rational normal curve.
.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Iitaka dimension of a line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
L on an algebraic variety X is the dimension of the image of the rational map to projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
determined by L. This is 1 less than the dimension of the ring
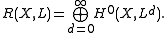
The Iitaka dimension of L is always less than or equal to the dimension of X. If L is not effective, then its Iitaka dimension is defined to be
 (or sometimes −1).
(or sometimes −1).Big line bundles
A line bundle is big if it is of maximal Iitaka dimension, that is, if its Iitaka dimension is equal to the dimension of the underlying variety. Bigness is a birational invariant: If f : Y → X is a birational morphism of varieties, and if L is a big line bundle on X, then f*L is a big line bundle on Y.All ample line bundles are big.
Big line bundles need not determine birational isomorphisms of X with its image. For example, if C is a curve of genus 2, then the canonical bundle KC is big, but it determines a two-to-one covering, a morphism C to its image as canonical curve, which here is a rational normal curve.
Kodaira dimension
The Iitaka dimension of the canonical bundle of a smooth variety is called its Kodaira dimensionKodaira dimension
In algebraic geometry, the Kodaira dimension κ measures the size of the canonical model of a projective variety V.The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar.-The plurigenera:...
.

