Infinitary combinatorics
Encyclopedia
In mathematics, infinitary combinatorics, or combinatorial set theory, is an extension of ideas in combinatorics
to infinite sets.
Some of the things studied include continuous graphs and trees
, extensions of Ramsey's theorem
, and Martin's axiom
.
Recent developments concern combinatorics of the continuum and combinatorics on successors of singular cardinals.
and n for a natural number. introduced the notation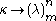
as a shorthand way of saying that every partition
of the set [κ]n of n-element subsets of
into m pieces has a homogeneous set of order type λ. A homogeneous set is in this case a subset of κ such that every n-element subset is in the same element of the partition. When m is 2 it is often omitted.
There are no ordinals κ with κ→(ω)ω, so n is usually taken to be finite. An extension where n is almost allowed to be infinite is
the notation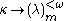
which is a shorthand way of saying that every partition
of the set of finite subsets of κ into m pieces has a subset of order type λ such that for any finite n, all subsets of size n are in the same element of the partition. When m is 2 it is often omitted.
Another variation is the notation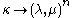
which is a shorthand way of saying that every coloring of the set [κ]n of n-element subsets of κ with 2 colors has a subset of order type λ such that all elements of [λ]n have the first color, or a subset of order type μ such that all elements of [μ]n have the second color.
Some properties of this include: (in what follows
is a cardinal)
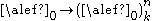for all finite n and k (Ramsey's theorem
).
(Erdős–Rado theorem
.)
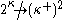(Sierpiński theorem)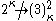
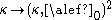(Erdős–Dushnik–Miller theorem).
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
to infinite sets.
Some of the things studied include continuous graphs and trees
Tree (set theory)
In set theory, a tree is a partially ordered set In set theory, a tree is a partially ordered set (poset) In set theory, a tree is a partially ordered set (poset) (T, In set theory, a tree is a partially ordered set (poset) (T, ...
, extensions of Ramsey's theorem
Ramsey's theorem
In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
, and Martin's axiom
Martin's axiom
In the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
.
Recent developments concern combinatorics of the continuum and combinatorics on successors of singular cardinals.
Ramsey theory for infinite sets
Write κ, λ for ordinals, m for a cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
and n for a natural number. introduced the notation
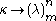
as a shorthand way of saying that every partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the set [κ]n of n-element subsets of
into m pieces has a homogeneous set of order type λ. A homogeneous set is in this case a subset of κ such that every n-element subset is in the same element of the partition. When m is 2 it is often omitted.There are no ordinals κ with κ→(ω)ω, so n is usually taken to be finite. An extension where n is almost allowed to be infinite is
the notation
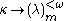
which is a shorthand way of saying that every partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the set of finite subsets of κ into m pieces has a subset of order type λ such that for any finite n, all subsets of size n are in the same element of the partition. When m is 2 it is often omitted.
Another variation is the notation
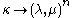
which is a shorthand way of saying that every coloring of the set [κ]n of n-element subsets of κ with 2 colors has a subset of order type λ such that all elements of [λ]n have the first color, or a subset of order type μ such that all elements of [μ]n have the second color.
Some properties of this include: (in what follows
is a cardinal)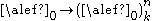 for all finite n and k (Ramsey's theoremRamsey's theorem
In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
).
(Erdős–Rado theoremErdős–Rado theorem
In partition calculus, part of combinatorial set theory, which is a branch of mathematics, the Erdős–Rado theorem is a basic result, extending Ramsey's theorem to uncountable sets.-Statement of the theorem:If r≥2 is finite, κ is an infinite cardinal, then...
.)
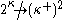(Sierpiński theorem)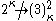 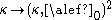(Erdős–Dushnik–Miller theorem).Large cardinals
Several large cardinal properties can be defined using this notation. In particular:- Weakly compact cardinalWeakly compact cardinalIn mathematics, a weakly compact cardinal is a certain kind of cardinal number introduced by ; weakly compact cardinals are large cardinals, meaning that their existence can not be proven from the standard axioms of set theory....
s κ are those that satisfy κ→(κ)2 - α-Erdős cardinalErdos cardinalIn mathematics, an Erdős cardinal, also called a partition cardinal is a certain kind of large cardinal number introduced by .The Erdős cardinal κ is defined to be the least cardinal such that for every function...
s κ are the smallest that satisfy κ→(α)<ω - Ramsey cardinalRamsey cardinalIn mathematics, a Ramsey cardinal is a certain kind of large cardinal number introduced by and named after Frank P. Ramsey.With [κ]<ω denoting the set of all finite subsets of κ, a cardinal number κ such that for every function...
s κ are those that satisfy κ→(κ)<ω