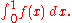Information-based complexity
Encyclopedia
Information-based complexity (IBC) studies optimal algorithms and computational complexity
for the continuous problems which arise in physical science
, economics
, engineering
, and mathematical finance
. IBC has studied such continuous problems as path integration
, partial differential equations, systems of ordinary differential equations, nonlinear equations, integral equations, fixed points
, and very high-dimensional integration
. All these problems involve functions (typically multivariate) of a real or complex variable. Since one can never obtain a closed-form solution of the problems of interest one has to settle for a numerical solution. Since a function of a real or complex variable cannot be entered into a digital computer, the solution of continuous problems involves partial information. To give a simple illustration, in the numerical approximation of an integral, only samples of the integrand at a finite number of points are available. In the numerical solution of partial differential equations the functions specifying the boundary conditions and the coefficients of the differential operator can only be sampled. Furthermore, this partial information can be expensive to obtain. Finally the information is often contaminated by noise.
The goal of information-based complexity is to create a theory of computational complexity and optimal algorithms for problems with partial, contaminated and priced information, and to apply the results to answering questions in various disciplines. Examples of such disciplines include physics
, economics, mathematical finance, computer vision
, control theory
, geophysics
, medical imaging
, weather forecasting
and climate prediction
, and statistics
. The theory is developed over abstract spaces, typically Hilbert
or Banach
spaces, while the applications are usually for multivariate problems.
Since the information is partial and contaminated, only approximate solutions can be obtained. IBC studies computational complexity and optimal algorithms for approximate solutions in various settings. Since the worst case setting often leads to negative results such as unsolvability and intractability, settings with weaker assurances such as average, probabilistic and randomized are also studied. A fairly new area of IBC research is continuous quantum computing.
For most integrands we can't use the fundamental theorem of calculus
to compute the integral analytically; we have to approximate it numerically. We compute the values of
at n points
The n numbers are the partial information about the true integrand
We combine these n numbers by a combinatory algorithm to compute an approximation to the integral. See the monograph Complexity and Information for particulars.
Because we have only partial information we can use an adversary argument to tell us how large n has to be to compute an
-approximation. Because of these information-based arguments we can often obtain tight bounds on the complexity of continuous problems. For discrete problems such as integer factorization
or the travelling salesman problem
we have settle for conjectures about the complexity hierarchy. The reason is that the input is a number or a vector of numbers and can thus be entered into the computer. Thus there is typically no adversary argument at the information level and the complexity of a discrete problem is rarely known.
The univariate integration problem was for illustration only. Significant for many applications is multivariate integration. The number of variables is in the hundreds or thousands. The number of variables may even be infinite; we then speak of path integration. The reason that integrals are important in many disciplines is that they occur when we want to know the expected behavior of a continuous process. See for example, the application to mathematical finance below.
Assume we want to compute an integral in d dimensions (dimensions and variables are used interchangeably) and that we want to guarantee an error at most
for any integrand in some class. The computational complexity of the problem is known to be of order 
(Here we are counting the number of function evaluations and the number of arithmetic operations so this is the time complexity.) This would take many years for even modest values of 
The exponential dependence on d is called the curse of dimensionality
. We say the problem is intractable.
We stated the curse of dimensionality for integration. But exponential dependence on d occurs for almost every continuous problem that has been investigated. How can we try to vanquish the curse? There are two possibilities:
(CMO) requires the calculation of a number of
dimensional integrals, the 
being the number of months in 
years. Recall that if a worst case assurance is required the time is of order 
time units. Even if the error is not small, say 
this is 
time units. People in finance have long been using the Monte Carlo method
(MC), an instance of a randomized algorithm. Then in 1994 a research group at Columbia University
(Papageorgiou, Paskov, Traub, Woźniakowski) discovered that the quasi-Monte Carlo
(QMC) method using low discrepancy sequences
beat MC by one to three orders of magnitude. The results were reported to a number of Wall Street finance to considerable initial skepticism. The results were first published by Paskov and Traub
, Faster Valuation of Financial Derivatives, Journal of Portfolio Management 22, 113-120. Today QMC is widely used in the financial sector to value financial derivatives.
These results are empirical; where does computational complexity come in? QMC is not a panacea for all high dimensional integrals. What is special about financial derivatives? Here's a possible explanation. The
dimensions in the CMO represent monthly future times. Due to the discounted value of money variables representing times for in the future are less important than the variables representing nearby times. Thus the integrals are non-isotropic. Sloan and Woźniakowski introduced the very powerful idea of weighted spaces which is a formalization of the above observation. They were able to show that with this additional domain knowledge high dimensional integrals satisfying certain conditions were tractable even in the worst case! In contrast the Monte Carlo method gives only a stochastic assurance. See Sloan and Woźniakowski When are Quasi-Monte Carlo Algorithms Efficient for High Dimensional Integration? J. Complexity 14, 1-33, 1998. For which classes of integrals is QMC superior to MC? This continues to be a major research problem.
had the key insight that the optimal algorithm and the computational complexity of solving a continuous problem depended on the available information. He applied this insight to the solution of nonlinear equations
which started the area of optimal iteration theory. This research was published in the 1964 monograph Iterative Methods for the Solution of Equations.
The general setting for information-based complexity was formulated by Traub and Woźniakowski in 1980 in A General Theory of Optimal Algorithms. For a list of more recent monographs and pointers to the extensive literature see To Learn More below.
Extensive bibliographies may be found in the monographs N (1988), TW (1980), TWW (1988) and TW (1998).
The IBC website has a searchable data base of some 730 items.
Listings of papers may be found in many of the homepages.
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
for the continuous problems which arise in physical science
Physical science
Physical science is an encompassing term for the branches of natural science and science that study non-living systems, in contrast to the life sciences...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, and mathematical finance
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
. IBC has studied such continuous problems as path integration
Path integration
Path integration is the name given to the method thought to be used by animals for dead reckoning.Charles Darwin and J.J. Murphy first postulated an inertially-based navigation system in animals in 1873...
, partial differential equations, systems of ordinary differential equations, nonlinear equations, integral equations, fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, and very high-dimensional integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
. All these problems involve functions (typically multivariate) of a real or complex variable. Since one can never obtain a closed-form solution of the problems of interest one has to settle for a numerical solution. Since a function of a real or complex variable cannot be entered into a digital computer, the solution of continuous problems involves partial information. To give a simple illustration, in the numerical approximation of an integral, only samples of the integrand at a finite number of points are available. In the numerical solution of partial differential equations the functions specifying the boundary conditions and the coefficients of the differential operator can only be sampled. Furthermore, this partial information can be expensive to obtain. Finally the information is often contaminated by noise.
The goal of information-based complexity is to create a theory of computational complexity and optimal algorithms for problems with partial, contaminated and priced information, and to apply the results to answering questions in various disciplines. Examples of such disciplines include physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, economics, mathematical finance, computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, geophysics
Geophysics
Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...
, medical imaging
Medical imaging
Medical imaging is the technique and process used to create images of the human body for clinical purposes or medical science...
, weather forecasting
Weather forecasting
Weather forecasting is the application of science and technology to predict the state of the atmosphere for a given location. Human beings have attempted to predict the weather informally for millennia, and formally since the nineteenth century...
and climate prediction
Numerical weather prediction
Numerical weather prediction uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic...
, and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
. The theory is developed over abstract spaces, typically Hilbert
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
or Banach
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
spaces, while the applications are usually for multivariate problems.
Since the information is partial and contaminated, only approximate solutions can be obtained. IBC studies computational complexity and optimal algorithms for approximate solutions in various settings. Since the worst case setting often leads to negative results such as unsolvability and intractability, settings with weaker assurances such as average, probabilistic and randomized are also studied. A fairly new area of IBC research is continuous quantum computing.
Overview
We illustrate some important concepts with a very simple example, the computation of
For most integrands we can't use the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
to compute the integral analytically; we have to approximate it numerically. We compute the values of
at n points
The n numbers are the partial information about the true integrand
We combine these n numbers by a combinatory algorithm to compute an approximation to the integral. See the monograph Complexity and Information for particulars.Because we have only partial information we can use an adversary argument to tell us how large n has to be to compute an
-approximation. Because of these information-based arguments we can often obtain tight bounds on the complexity of continuous problems. For discrete problems such as integer factorizationInteger factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
or the travelling salesman problem
Travelling salesman problem
The travelling salesman problem is an NP-hard problem in combinatorial optimization studied in operations research and theoretical computer science. Given a list of cities and their pairwise distances, the task is to find the shortest possible tour that visits each city exactly once...
we have settle for conjectures about the complexity hierarchy. The reason is that the input is a number or a vector of numbers and can thus be entered into the computer. Thus there is typically no adversary argument at the information level and the complexity of a discrete problem is rarely known.
The univariate integration problem was for illustration only. Significant for many applications is multivariate integration. The number of variables is in the hundreds or thousands. The number of variables may even be infinite; we then speak of path integration. The reason that integrals are important in many disciplines is that they occur when we want to know the expected behavior of a continuous process. See for example, the application to mathematical finance below.
Assume we want to compute an integral in d dimensions (dimensions and variables are used interchangeably) and that we want to guarantee an error at most
for any integrand in some class. The computational complexity of the problem is known to be of order (Here we are counting the number of function evaluations and the number of arithmetic operations so this is the time complexity.) This would take many years for even modest values of The exponential dependence on d is called the curse of dimensionalityCurse of dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
. We say the problem is intractable.
We stated the curse of dimensionality for integration. But exponential dependence on d occurs for almost every continuous problem that has been investigated. How can we try to vanquish the curse? There are two possibilities:
- We can weaken the guarantee that the error must be less than
(worst case setting) and settle for a stochastice assurance. For example, we might only require that the expected error be less than 
(average case setting.) Another possibility is the randomized setting. For some problems we can break the curse of dimensionality by weakening the assurance; for others, we cannot. There is a large IBC literature on results in various settings; see Where to Learn More below. - We can incorporate domain knowledge. See An Example: Mathematical Finance below.
An example: mathematical finance
Very high dimensional integrals are common in finance. For example, computing expected cash flows for a collateralized mortgage obligationCollateralized mortgage obligation
A collateralized mortgage obligation is a type of financial debt vehicle that was first created in 1983 by the investment banks Salomon Brothers and First Boston for U.S. mortgage lender Freddie Mac. A collateralized mortgage obligation (CMO) is a type of financial debt vehicle that was first...
(CMO) requires the calculation of a number of
dimensional integrals, the being the number of months in years. Recall that if a worst case assurance is required the time is of order time units. Even if the error is not small, say this is time units. People in finance have long been using the Monte Carlo methodMonte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
(MC), an instance of a randomized algorithm. Then in 1994 a research group at Columbia University
Columbia University
Columbia University in the City of New York is a private, Ivy League university in Manhattan, New York City. Columbia is the oldest institution of higher learning in the state of New York, the fifth oldest in the United States, and one of the country's nine Colonial Colleges founded before the...
(Papageorgiou, Paskov, Traub, Woźniakowski) discovered that the quasi-Monte Carlo
Quasi-Monte Carlo method
In numerical analysis, a quasi-Monte Carlo method is a method for the computation of an integral that is based on low-discrepancy sequences...
(QMC) method using low discrepancy sequences
Low-discrepancy sequence
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy....
beat MC by one to three orders of magnitude. The results were reported to a number of Wall Street finance to considerable initial skepticism. The results were first published by Paskov and Traub
Joseph F Traub
Joseph Frederick Traub , is a computer scientist. He is the Edwin Howard Armstrong Professor of Computer Science at Columbia University and External Professor at the Santa Fe Institute...
, Faster Valuation of Financial Derivatives, Journal of Portfolio Management 22, 113-120. Today QMC is widely used in the financial sector to value financial derivatives.
These results are empirical; where does computational complexity come in? QMC is not a panacea for all high dimensional integrals. What is special about financial derivatives? Here's a possible explanation. The
dimensions in the CMO represent monthly future times. Due to the discounted value of money variables representing times for in the future are less important than the variables representing nearby times. Thus the integrals are non-isotropic. Sloan and Woźniakowski introduced the very powerful idea of weighted spaces which is a formalization of the above observation. They were able to show that with this additional domain knowledge high dimensional integrals satisfying certain conditions were tractable even in the worst case! In contrast the Monte Carlo method gives only a stochastic assurance. See Sloan and Woźniakowski When are Quasi-Monte Carlo Algorithms Efficient for High Dimensional Integration? J. Complexity 14, 1-33, 1998. For which classes of integrals is QMC superior to MC? This continues to be a major research problem.Brief history
Precursors to IBC may be found in the 1950s by Kiefer, Sard, and Nikolskij. In 1959 TraubJoseph F Traub
Joseph Frederick Traub , is a computer scientist. He is the Edwin Howard Armstrong Professor of Computer Science at Columbia University and External Professor at the Santa Fe Institute...
had the key insight that the optimal algorithm and the computational complexity of solving a continuous problem depended on the available information. He applied this insight to the solution of nonlinear equations
Nonlinearity
In mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...
which started the area of optimal iteration theory. This research was published in the 1964 monograph Iterative Methods for the Solution of Equations.
The general setting for information-based complexity was formulated by Traub and Woźniakowski in 1980 in A General Theory of Optimal Algorithms. For a list of more recent monographs and pointers to the extensive literature see To Learn More below.
Prizes
There are a number of prizes for IBC research.- Prize for Achievement in Information-Based Complexity This annual prize, which was created in 1999, consists of $3000 and a plaque. It is given for outstanding achievement in information-based complexity. The recipients are listed below. The affiliation is as of the time of the award.
- 1999 Erich Novak, University of Jena, Germany
- 2000 Sergei Pereverzev, Ukrainian Academy of Science, Ukraine
- 2001 G. W. Wasilkowski, University of Kentucky, USA
- 2002 Stefan Heinrich, University of Kaiserslautern, Germany
- 2003 Arthur G. Werschulz, Fordham University, USA
- 2004 Peter Mathe, Weierstrass Institute for Applied Analysis and Stochastics, Germany
- 2005 Ian Sloan, Scientia Professor, University of New South Wales, Sydney, Australia
- 2006 Leszek Plaskota, Department of Mathematics, Informatics and Mechanics, University of Warsaw, Poland
- 2007 Klaus Ritter, Department of Mathematics, TU Darmstadt, Germany
- 2008 Anargyros Papageorgiou, Columbia University, USA
- Information-Based Complexity Young Researcher Award This annual award, which created in 2003, consists of $1000 and a plaque. The recipients have been
- 2003 Frances Kuo, School of Mathematics, University of New South Wales, Sydney, Australia
- 2004 Christiane Lemieux, University of Calgary, Calgary, Alberta, Canada, and Josef Dick, University of New South Wales, Sydney, Australia
- 2005 Friedrich Pillichshammer, Institute for Financial Mathematics, University of Linz, Austria
- 2006 Jakob Creutzig, TU Darmstadt, Germany and Dirk Nuyens, Katholieke Universiteit, Leuven, Belgium
- 2007 Andreas Neuenkirch, Universität Frankfurt, Germany
- Best Paper Award, Journal of Complexity This annual award, which was created in 1996, consists of $3000 and a plaque. Many, but by no means all of the awards have been for research in IBC. The recipients have been
- 1996 Pascal Koiran
- 1997 Co-winners
- B. Bank, M. Giusti, J. Heintz, and G. M. Mbakop
- R. DeVore and V. Temlyakov
- 1998 Co-winners
- Stefan Heinrich
- P. Kirrinis
- 1999 Arthur G. Werschulz
- 2000 Co-winners
- Bernard Mourrain and Victor Y. Pan
- J. Maurice Rojas
- 2001 Erich Novak
- 2002 Peter Hertling
- 2003 Co-winners
- Markus Blaeser
- Boleslaw Kacewicz
- 2004 Stefan Heinrich
- 2005 Co-winners
- Yosef Yomdin
- Josef Dick and Friedrich Pillichshammer
- 2006 Knut Petras and Klaus Ritter
- 2007 Co-winners
- Martin Avendano, Teresa Krick and Martin Sombra
- Istvan Berkes, Robert F. Tichy and the late Walter Philipp
- 2008 Stefan Heinrich and Bernhard Milla
Monographs
The following list is in chronologial order- Traub, J. F., Iterative Methods for the Solution of Equations, Prentice Hall, 1964. Reissued Chelsea Publishing Company, 1982; Russian translation MIR, 1985; Reissued American Mathematical Society, 1998
- Traub, J. F., and Woźniakowski, H., A General Theory of Optimal Algorithms, Academic Press, New York, 1980
- Traub, J. F., Woźniakowski, H., and Wasilkowski, G. W., Information, Uncertainty, Complexity, Addison-Wesley, New York, 1983
- Novak, E., Deterministic and Stochastic Error Bounds in Numerical Analysis, Lecture Nots in Mathematics, vol. 1349, Springer-Verlag, New York, 1988
- Traub, J. F., Woźniakowski, H., and Wasilkowski, G. W., Information-Based Complexity, Academic Press, New York, 1988
- Werschulz, A. G., The Computational Complexity of Differential and Integral Equations: An Information-Based Approach, Oxford University Press, New York, 1991
- Kowalski, M., Sikorski, K., and Stenger, F., Selected Topics in Approximation and Computation, Oxford University Press, Oxford, UK, 1995
- Plaskota, L., Noisy Information and Computational Complexity, Cambridge University Press, Cambridge, UK, 1996
- Traub, J. F., and Werschulz, A. G., Complexity and Information, Oxford University Press, Oxford, UK, 1998
- Ritter, K., Average-Case Analysis of Numerical Problems, Springer-Verlag, New York, 2000
- Sikorski, K., Optimal Solution of Nonlinear Equations, Oxford University Press, Oxford, UK, 2001
Pointers to the literature
The Journal of Complexity publishes many IBC papers.Extensive bibliographies may be found in the monographs N (1988), TW (1980), TWW (1988) and TW (1998).
The IBC website has a searchable data base of some 730 items.
Listings of papers may be found in many of the homepages.
External links
- IBC website This has searchable data base of some 730 items
- Journal of Complexity
- Complexity and Information
- Joseph Traub
- Henryk Woźniakowski
- J.F Traub, 1985. An Introduction to Information-Based Complexity