
Integrability conditions for differential systems
Encyclopedia
In mathematics
, certain systems of partial differential equation
s are usefully formulated, from the point of view of their underlying geometric and algebraic structure, in terms of a system of differential form
s. The idea is to take advantage of the way a differential form restricts to a submanifold
, and the fact that this restriction is compatible with the exterior derivative
. This is one possible approach to certain over-determined systems, for example. A Pfaffian system is one specified by 1-forms alone, but the theory includes other types of example of differential system.
Given a collection of differential 1-forms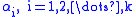 on an n-dimensional manifold M,
on an n-dimensional manifold M,
an integral manifold is a submanifold whose tangent space at every point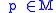 is annihilated by each
is annihilated by each 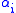 .
.
A maximal integral manifold is a submanifold

such that the kernel of the restriction map on forms

is spanned by the at every point p of N. If in addition the
at every point p of N. If in addition the 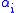 are linearly independent, then N is (n − k)-dimensional. Note that
are linearly independent, then N is (n − k)-dimensional. Note that  need not be an embedded submanifold.
need not be an embedded submanifold.
A Pfaffian system is said to be completely integrable if N admits a foliation
by maximal integral manifolds. (Note that the foliation need not be regular; i.e. the leaves of the foliation might not be embedded submanifolds.)
An integrability condition is a condition on the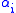 to guarantee that there will be integral submanifolds of sufficiently high dimension.
to guarantee that there will be integral submanifolds of sufficiently high dimension.
. One version states that if the ideal algebraically generated by the collection of
algebraically generated by the collection of 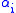 inside the ring
inside the ring 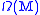 is differentially closed, in other words
is differentially closed, in other words
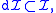
then the system admits a foliation
by maximal integral manifolds. (The converse is obvious from the definitions.)
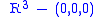

If were in the ideal generated by
were in the ideal generated by  we would have, by the skewness of the wedge product
we would have, by the skewness of the wedge product

But a direct calculation gives

which is a nonzero multiple of the standard volume form on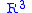 . Therefore, there are no two-dimensional leaves, and the system is not completely integrable.
. Therefore, there are no two-dimensional leaves, and the system is not completely integrable.
On the other hand, the curve defined by
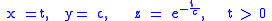
is easily verified to be a solution (i.e. an integral curve
) for the above Pfaffian system for any nonzero constant .
.
, we may consider the problem of finding an orthogonal coframe
 (i.e., collection of 1-forms forming a basis of the cotangent space at every point with
(i.e., collection of 1-forms forming a basis of the cotangent space at every point with  ) which are closed
) which are closed 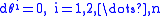 . By the Poincaré lemma, the
. By the Poincaré lemma, the 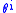 locally will have the form
locally will have the form 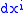 for some functions
for some functions  on the manifold, and thus provide an isometry of an open subset of M with an open subset of
on the manifold, and thus provide an isometry of an open subset of M with an open subset of 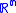 . Such a manifold is called locally flat.
. Such a manifold is called locally flat.
This problem reduces to a question on the coframe bundle
of M. Suppose we had such a closed coframe
 .
.
If we had another coframe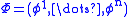 , then the two coframes would be related by an orthogonal transformation
, then the two coframes would be related by an orthogonal transformation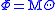
If the connection 1-form is , then we have
, then we have
On the other hand,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, certain systems of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s are usefully formulated, from the point of view of their underlying geometric and algebraic structure, in terms of a system of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s. The idea is to take advantage of the way a differential form restricts to a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
, and the fact that this restriction is compatible with the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
. This is one possible approach to certain over-determined systems, for example. A Pfaffian system is one specified by 1-forms alone, but the theory includes other types of example of differential system.
Given a collection of differential 1-forms
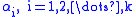 on an n-dimensional manifold M,
on an n-dimensional manifold M,an integral manifold is a submanifold whose tangent space at every point
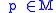 is annihilated by each
is annihilated by each 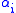 .
.A maximal integral manifold is a submanifold

such that the kernel of the restriction map on forms

is spanned by the
 at every point p of N. If in addition the
at every point p of N. If in addition the 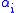 are linearly independent, then N is (n − k)-dimensional. Note that
are linearly independent, then N is (n − k)-dimensional. Note that  need not be an embedded submanifold.
need not be an embedded submanifold.A Pfaffian system is said to be completely integrable if N admits a foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
by maximal integral manifolds. (Note that the foliation need not be regular; i.e. the leaves of the foliation might not be embedded submanifolds.)
An integrability condition is a condition on the
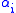 to guarantee that there will be integral submanifolds of sufficiently high dimension.
to guarantee that there will be integral submanifolds of sufficiently high dimension.Necessary and sufficient conditions
The necessary and sufficient conditions for complete integrability of a Pfaffian system are given by the Frobenius theoremFrobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
. One version states that if the ideal
 algebraically generated by the collection of
algebraically generated by the collection of 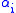 inside the ring
inside the ring 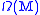 is differentially closed, in other words
is differentially closed, in other words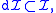
then the system admits a foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
by maximal integral manifolds. (The converse is obvious from the definitions.)
Example of a non-integrable system
Not every Pfaffian system is completely integrable in the Frobenius sense. For example, consider the following one-form on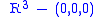

If
 were in the ideal generated by
were in the ideal generated by  we would have, by the skewness of the wedge product
we would have, by the skewness of the wedge product
But a direct calculation gives

which is a nonzero multiple of the standard volume form on
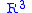 . Therefore, there are no two-dimensional leaves, and the system is not completely integrable.
. Therefore, there are no two-dimensional leaves, and the system is not completely integrable.On the other hand, the curve defined by
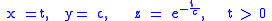
is easily verified to be a solution (i.e. an integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
) for the above Pfaffian system for any nonzero constant
 .
.Examples of applications
In Riemannian geometryRiemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, we may consider the problem of finding an orthogonal coframe
Coframe
In mathematics, a coframe or coframe field on a smooth manifold M is a system of one-forms or covectors which form a basis of the cotangent bundle at every point. In the exterior algebra of M, one has a natural map from v_k:\bigoplus^kT^*M\to\bigwedge^kT^*M, given by v_k:\mapsto...
 (i.e., collection of 1-forms forming a basis of the cotangent space at every point with
(i.e., collection of 1-forms forming a basis of the cotangent space at every point with  ) which are closed
) which are closed 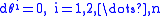 . By the Poincaré lemma, the
. By the Poincaré lemma, the 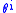 locally will have the form
locally will have the form 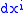 for some functions
for some functions  on the manifold, and thus provide an isometry of an open subset of M with an open subset of
on the manifold, and thus provide an isometry of an open subset of M with an open subset of 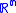 . Such a manifold is called locally flat.
. Such a manifold is called locally flat.This problem reduces to a question on the coframe bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of M. Suppose we had such a closed coframe
 .
.If we had another coframe
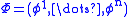 , then the two coframes would be related by an orthogonal transformation
, then the two coframes would be related by an orthogonal transformation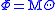
If the connection 1-form is
 , then we have
, then we have
On the other hand,
-

But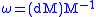 is the Maurer–Cartan form for the orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
is the Maurer–Cartan form for the orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
. Therefore it obeys the structural equation

and this is just the curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of M:

After an application of the Frobenius theorem, one concludes that a manifold M is locally flat if and only if its curvature vanishes.
Generalizations
Many generalizations exist to integrability conditions on differential systems which are not necessarily generated by one-forms. The most famous of which are the Cartan-Kähler theorem, which only works for real analyticReal analysisReal analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
differential systems, and the Cartan–Kuranishi prolongation theorem. See Further reading for details.
Further reading
- Bryant, Chern, Gardner, Goldschmidt, Griffiths, Exterior Differential Systems, Mathematical Sciences Research Institute Publications, Springer-Verlag, ISBN 0-387-97411-3
- Olver, P., Equivalence, Invariants, and Symmetry, Cambridge, ISBN 0-521-47811-1
- Ivey, T., Landsberg, J.M., Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Differential Systems, American Mathematical Society, ISBN 0-8218-3375-8

