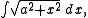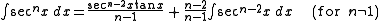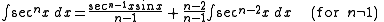Integral of secant cubed
Encyclopedia
The integral of secant cubed is one of the more challenging indefinite integrals of elementary calculus
:
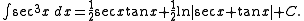
There are a number of reasons why this particular antiderivative is worthy of special attention:
may be found by integration by parts
, as follows:
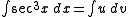
where
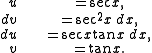
Then

Here we have assumed already known the integral of the secant function
.
Next we add to both sides of the equality just derived:
to both sides of the equality just derived:
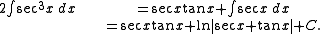
Then divide both sides by 2:
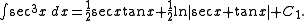
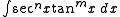 can be reduced using the Pythagorean identity if n is even or n and m are both odd. If n is odd and m is even, hyperbolic substitutions can be used to replace the nested integration by parts with hyperbolic power reducing formulas.
can be reduced using the Pythagorean identity if n is even or n and m are both odd. If n is odd and m is even, hyperbolic substitutions can be used to replace the nested integration by parts with hyperbolic power reducing formulas.
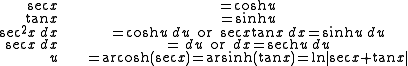
Note that follows directly from this substitution.
follows directly from this substitution.
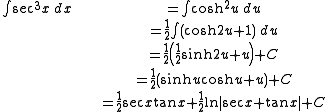
Alternatively:
Even powers of tangents can be accommodated by using binomial expansion to form an odd polynomial of secant and using these formulae on the largest term and combining like terms.
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
:
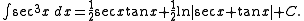
There are a number of reasons why this particular antiderivative is worthy of special attention:
- The technique used for reducing integrals of higher odd powers of secant to lower ones is fully present in this, the simplest case. The other cases are done in the same way.
- The utility of hyperbolic functions in integration can be demonstrated in cases of odd powers of secant (powers of tangent can also be included).
- This is one of several integrals usually done in a first-year calculus course in which the most natural way to proceed involves integrating by parts and returning to the same integral one started with (another is the integral of the product of an exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
with a sine or cosine function; yet another the integral of a power of the sine or cosine function).
- This integral is used in evaluating any integral of the form
-
-
- where a is a constant. In particular, it appears in the problems of:
- rectifying (i.e. finding the arc lengthArc lengthDetermining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
of) the parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. - rectifying the Archimedean spiralArchimedean spiralThe Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
. - finding the surface areaSurface areaSurface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
of the helicoidHelicoidThe helicoid, after the plane and the catenoid, is the third minimal surface to be known. It was first discovered by Jean Baptiste Meusnier in 1776. Its name derives from its similarity to the helix: for every point on the helicoid there is a helix contained in the helicoid which passes through...
.
Derivation
This antiderivativeAntiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
may be found by integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
, as follows:
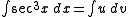
where
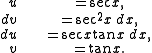
Then

Here we have assumed already known the integral of the secant function
Integral of the secant function
The integral of the secant function of trigonometry was the subject of one of the "outstanding open problems of the mid-seventeenth century", solved in 1668 by James Gregory. In 1599, Edward Wright evaluated the integral by numerical methods – what today we would call Riemann sums...
.
Next we add
 to both sides of the equality just derived:
to both sides of the equality just derived: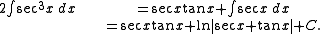
Then divide both sides by 2:
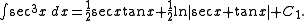
Hyperbolic derivation
Integrals of the form: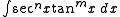 can be reduced using the Pythagorean identity if n is even or n and m are both odd. If n is odd and m is even, hyperbolic substitutions can be used to replace the nested integration by parts with hyperbolic power reducing formulas.
can be reduced using the Pythagorean identity if n is even or n and m are both odd. If n is odd and m is even, hyperbolic substitutions can be used to replace the nested integration by parts with hyperbolic power reducing formulas.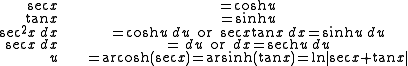
Note that
 follows directly from this substitution.
follows directly from this substitution.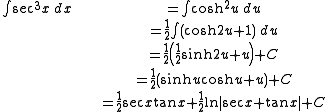
Higher odd powers of secant
Just as the integration by parts above reduced the integral of secant cubed to the integral of secant to the first power, so a similar process reduces the integral of higher odd powers of secant to lower ones. This is the secant reduction formula, which follows the syntax:Alternatively:
Even powers of tangents can be accommodated by using binomial expansion to form an odd polynomial of secant and using these formulae on the largest term and combining like terms.