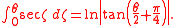Integral of the secant function
Encyclopedia
The integral
of the secant function of trigonometry
was the subject of one of the "outstanding open problems of the mid-seventeenth century", solved in 1668 by James Gregory. In 1599, Edward Wright
evaluated the integral by numerical methods – what today we would call Riemann sum
s. He wanted the solution for the purposes of cartography
– specifically for constructing an accurate Mercator map
. In the 1640s, Henry Bond, a teacher of navigation, surveying, and other mathematical topics, compared Wright's numerically computed table of values of the integral of the secant with a table of logarithms of the tangent function, and consequently conjectured that
That conjecture became widely known, and in 1665, Isaac Newton
was aware of it.
The problem was solved by Isaac Barrow
. His proof of the result was the earliest use of partial fraction
s in integration. Adapted to modern notation, Barrow's proof began as follows:
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the secant function of trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
was the subject of one of the "outstanding open problems of the mid-seventeenth century", solved in 1668 by James Gregory. In 1599, Edward Wright
Edward Wright (mathematician)
Edward Wright was an English mathematician and cartographer noted for his book Certaine Errors in Navigation , which for the first time explained the mathematical basis of the Mercator projection, and set out a reference table giving the linear scale multiplication factor as a function of...
evaluated the integral by numerical methods – what today we would call Riemann sum
Riemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
s. He wanted the solution for the purposes of cartography
Cartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
– specifically for constructing an accurate Mercator map
Mercator projection
The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
. In the 1640s, Henry Bond, a teacher of navigation, surveying, and other mathematical topics, compared Wright's numerically computed table of values of the integral of the secant with a table of logarithms of the tangent function, and consequently conjectured that
That conjecture became widely known, and in 1665, Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
was aware of it.
The problem was solved by Isaac Barrow
Isaac Barrow
Isaac Barrow was an English Christian theologian, and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for the discovery of the fundamental theorem of calculus. His work centered on the properties of the tangent; Barrow was...
. His proof of the result was the earliest use of partial fraction
Partial fraction
In algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function ....
s in integration. Adapted to modern notation, Barrow's proof began as follows:
-
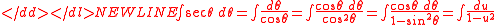
This reduces it to the problem of antidifferentiating a rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
by using partial fractions. The proof goes on from there:
-

Finally, we convert it back to a function of θ:
-
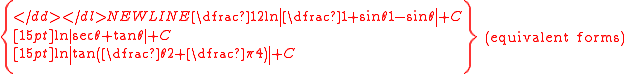
The problem can also be done by directly applying the Weierstrass substitutionWeierstrass substitutionIn integral calculus, the Weierstrass substitution, named after Karl Weierstrass, is used for finding antiderivatives, and hence definite integrals, of rational functions of trigonometric functions. No generality is lost by taking these to be rational functions of the sine and cosine. The...
, but the details become somewhat more complicated than in the argument above.
External links
-
-