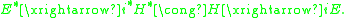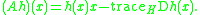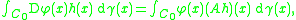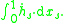Integration by parts operator
Encyclopedia
In mathematics
, an integration by parts operator is a linear operator used to formulate integration by parts
formulae; the most interesting examples of integration by parts operators occur in infinite-dimensional settings and find uses in stochastic analysis and its applications.
such that both E and its continuous dual space E∗ are separable spaces; let μ be a Borel measure on E. Let S be any (fixed) subset
of the class of functions defined on E. A linear operator A : S → L2(E, μ; R) is said to be an integration by parts operator for μ if
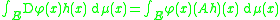
for every C1 function
φ : E → R and all h ∈ S for which either side of the above equality makes sense. In the above, Dφ(x) denotes the Fréchet derivative
of φ at x.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an integration by parts operator is a linear operator used to formulate integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
formulae; the most interesting examples of integration by parts operators occur in infinite-dimensional settings and find uses in stochastic analysis and its applications.
Definition
Let E be a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
such that both E and its continuous dual space E∗ are separable spaces; let μ be a Borel measure on E. Let S be any (fixed) subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the class of functions defined on E. A linear operator A : S → L2(E, μ; R) is said to be an integration by parts operator for μ if
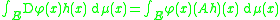
for every C1 function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
φ : E → R and all h ∈ S for which either side of the above equality makes sense. In the above, Dφ(x) denotes the Fréchet derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
of φ at x.
Examples
- Consider an abstract Wiener spaceAbstract Wiener spaceAn abstract Wiener space is a mathematical object in measure theory, used to construct a "decent" measure on an infinite-dimensional vector space. It is named after the American mathematician Norbert Wiener...
i : H → E with abstract Wiener measure γ. Take S to be the set of all C1 functions from E into E∗; E∗ can be thought of as a subspace of E in view of the inclusions
- For h ∈ S, define Ah by
- This operator A is an integration by parts operator, also known as the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
operator; a proof can be found in Elworthy (1974).
- The classical Wiener spaceClassical Wiener spaceIn mathematics, classical Wiener space is the collection of all continuous functions on a given domain , taking values in a metric space . Classical Wiener space is useful in the study of stochastic processes whose sample paths are continuous functions...
C0 of continuous pathsContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
in Rn starting at zero and defined on the unit intervalInterval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0, 1] has another integration by parts operator. Let S be the collection
- i.e., all boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
, adaptedAdapted processIn the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
processes with absolutely continuous sample paths. Let φ : C0 → R be any C1 function such that both φ and Dφ are bounded. For h ∈ S and λ ∈ R, the Girsanov theoremGirsanov theoremIn probability theory, the Girsanov theorem describes how the dynamics of stochastic processes change when the original measure is changed to an equivalent probability measure...
implies that
- Differentiating with respect to λ and setting λ = 0 gives
- where (Ah)(x) is the Itō integral
- The same relation holds for more general φ by an approximation argument; thus, the Itō integral is an integration by parts operator and can be seen as an infinite-dimensional divergence operator. This is the same result as the integration by parts formula derived from the Clark-Ocone theorem.