
Introduction to entropy
Encyclopedia
Entropy
is a measure of how evenly energy is distributed in a system. In a physical system, entropy provides a measure of the amount of energy that cannot be used to do work
.
When heat
flows from a hot region to a cold region, entropy increases as heat is distributed throughout the system. The concept of entropy is central to the second law of thermodynamics
. The second law determines which physical processes can occur. For example, it predicts that heat flows from high temperature to low temperature in spontaneous process
es. The second law of thermodynamics can be stated as saying that the entropy of an isolated system
always increases, and processes which increase entropy can occur spontaneously. Since entropy increases as uniformity increases, the second law says qualitatively that uniformity increases.
The term entropy was coined in 1865 by the German physicist Rudolf Clausius
, from the Greek words en-, "in", and trope "a turning", in analogy with energy
.
. It uses entropy to quantify the capacity of a system for change, namely that heat flows from a region of higher temperature to one with lower temperature, and to determine whether a thermodynamic process may occur.
Entropy is defined by two descriptions, first as macroscopic relationship between heat flow into a system and the system's change in temperature, and second, on a microscopic level, as the natural logarithm
of the number of microstates
of a system.
Following the formalism of Clausius, the first definition can be mathematically stated as:
Where dS is the change in entropy and δq is the heat added to the system reversibly. If the temperature is allowed to vary the equation must be integrated
over the temperature path. This definition of entropy does not allow the determination of an absolute value, only of differences.
The second definition of entropy comes from statistical mechanics
. The entropy of a particular macrostate
is defined to be Boltzmann constant times the natural logarithm
of the number of microstates corresponding to that macrostate, or mathematically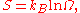
Where S is the entropy, kB is the Boltzmann constant, and Ω is the number of microstates.
The macrostate of a system is what we know about the system, for example the temperature
, pressure
, and volume of a gas in a box. For each set of values of temperature, pressure, and volume there are many arrangements of molecules which result in those values. The number of arrangements of molecules which could result in the same values for temperature, pressure and volume is the number of microstates.
The concept of energy
is related to the first law of thermodynamics
, which deals with the conservation of energy
and under which the loss in heat will result in a decrease in the internal energy
of the thermodynamic system
. Thermodynamic entropy provides a comparative measure of the amount of this decrease in internal energy of the system and the corresponding increase in internal energy of the surroundings at a given temperature. A simple and more concrete visualization of the second law is that energy of all types changes from being localized to becoming dispersed or spread out, if it is not hindered from doing so. Entropy change is the quantitative measure of that kind of a spontaneous process: how much energy has flowed or how widely it has become spread out at a specific temperature.
Entropy has been developed to describe any of several phenomena, depending on the field and the context in which it is being used. Information entropy
takes the mathematical concepts of statistical thermodynamics into areas of probability theory
unconnected with heat and energy.

at the melting temperature of ice. In this system, some heat
(δQ) from the warmer surroundings at 298 K (77°F, 25°C) transfers to the cooler system of ice and water at its constant temperature (T) of 273 K (32°F, 0°C), the melting temperature of ice. The entropy of the system, which is δQ/T, increases by δQ/273K. The heat δQ for this process is the energy required to change water from the solid state to the liquid state, and is called the enthalpy of fusion
, i.e. ΔH for ice fusion.
It is important to realize that the entropy of the surrounding room decreases less than the entropy of the ice and water increases: the room temperature of 298 K is larger than 273 K and therefore the ratio, (entropy change), of δQ/298K for the surroundings is smaller than the ratio (entropy change), of δQ/273K for the ice and water system. This is always true in spontaneous events in a thermodynamic system and it shows the predictive importance of entropy: the final net entropy after such an event is always greater than was the initial entropy.
As the temperature of the cool water rises to that of the room and the room further cools imperceptibly, the sum of the δQ/T over the continuous range, “at many increments”, in the initially cool to finally warm water can be found by calculus. The entire miniature ‘universe’, i.e. this thermodynamic system, has increased in entropy. Energy has spontaneously become more dispersed and spread out in that ‘universe’ than when the glass of ice + water was introduced and became a 'system' within it.
in developing statistical views of entropy
using probability theory
to describe the increased molecular movement on the microscopic level. That was before quantum behavior came to be better understood by Werner Heisenberg
and those who followed. Descriptions of thermodynamic (heat) entropy on the microscopic level are found in statistical thermodynamics and statistical mechanics
.
For most of the 20th century, textbooks tended to describe entropy as "disorder", following Boltzmann's early conceptualisation of the motional energy of molecules. More recently, there has been a trend in chemistry and physics textbooks to describe entropy in terms of "dispersal of energy". Entropy can also involve the dispersal of particles, which are themselves energetic. Thus there are instances where both particles and energy disperse at different rates when substances are mixed together.
The mathematics developed in statistical thermodynamics were found to be applicable in other disciplines. In particular, information sciences developed the concept of information entropy
where a constant replaces the temperature which is inherent in thermodynamic entropy.
The important overall principle is that ”Energy of all types changes from being localized to becoming dispersed or spread out, if it is not hindered from doing so. Entropy (or better, entropy change) is the quantitative measure of that kind of a spontaneous process: how much energy has been transferred/T or how widely it has become spread out at a specific temperature.
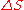 , was described in macroscopic terms that could be directly measured, such as volume, temperature, or pressure. However, today the classical equation of entropy,
, was described in macroscopic terms that could be directly measured, such as volume, temperature, or pressure. However, today the classical equation of entropy, 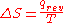 can be explained, part by part, in modern terms describing how molecules are responsible for what is happening:
can be explained, part by part, in modern terms describing how molecules are responsible for what is happening:
so that it provides "a measurement of the disorder or randomness of a system". It has been argued that ambiguities in the terms used (such as "disorder" and "chaos") contribute to widespread confusion and can hinder comprehension of entropy for most students. A more recent formulation associated with Frank L. Lambert
describing entropy as energy dispersal
describes entropy as measuring "the spontaneous dispersal of energy — at a specific temperature."
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
is a measure of how evenly energy is distributed in a system. In a physical system, entropy provides a measure of the amount of energy that cannot be used to do work
Work (thermodynamics)
In thermodynamics, work performed by a system is the energy transferred to another system that is measured by the external generalized mechanical constraints on the system. As such, thermodynamic work is a generalization of the concept of mechanical work in mechanics. Thermodynamic work encompasses...
.
When heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
flows from a hot region to a cold region, entropy increases as heat is distributed throughout the system. The concept of entropy is central to the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
. The second law determines which physical processes can occur. For example, it predicts that heat flows from high temperature to low temperature in spontaneous process
Spontaneous process
A spontaneous process is the time-evolution of a system in which it releases free energy and moves to a lower, more thermodynamically stable energy state...
es. The second law of thermodynamics can be stated as saying that the entropy of an isolated system
Isolated system
In the natural sciences an isolated system, as contrasted with an open system, is a physical system without any external exchange. If it has any surroundings, it does not interact with them. It obeys in particular the first of the conservation laws: its total energy - mass stays constant...
always increases, and processes which increase entropy can occur spontaneously. Since entropy increases as uniformity increases, the second law says qualitatively that uniformity increases.
The term entropy was coined in 1865 by the German physicist Rudolf Clausius
Rudolf Clausius
Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...
, from the Greek words en-, "in", and trope "a turning", in analogy with energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
.
Explanation
The concept of thermodynamic entropy arises from the second law of thermodynamicsSecond law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
. It uses entropy to quantify the capacity of a system for change, namely that heat flows from a region of higher temperature to one with lower temperature, and to determine whether a thermodynamic process may occur.
Entropy is defined by two descriptions, first as macroscopic relationship between heat flow into a system and the system's change in temperature, and second, on a microscopic level, as the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of the number of microstates
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
of a system.
Following the formalism of Clausius, the first definition can be mathematically stated as:
Where dS is the change in entropy and δq is the heat added to the system reversibly. If the temperature is allowed to vary the equation must be integrated
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over the temperature path. This definition of entropy does not allow the determination of an absolute value, only of differences.
The second definition of entropy comes from statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. The entropy of a particular macrostate
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
is defined to be Boltzmann constant times the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of the number of microstates corresponding to that macrostate, or mathematically
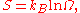
Where S is the entropy, kB is the Boltzmann constant, and Ω is the number of microstates.
The macrostate of a system is what we know about the system, for example the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, and volume of a gas in a box. For each set of values of temperature, pressure, and volume there are many arrangements of molecules which result in those values. The number of arrangements of molecules which could result in the same values for temperature, pressure and volume is the number of microstates.
The concept of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
is related to the first law of thermodynamics
First law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
, which deals with the conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
and under which the loss in heat will result in a decrease in the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of the thermodynamic system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
. Thermodynamic entropy provides a comparative measure of the amount of this decrease in internal energy of the system and the corresponding increase in internal energy of the surroundings at a given temperature. A simple and more concrete visualization of the second law is that energy of all types changes from being localized to becoming dispersed or spread out, if it is not hindered from doing so. Entropy change is the quantitative measure of that kind of a spontaneous process: how much energy has flowed or how widely it has become spread out at a specific temperature.
Entropy has been developed to describe any of several phenomena, depending on the field and the context in which it is being used. Information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
takes the mathematical concepts of statistical thermodynamics into areas of probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
unconnected with heat and energy.

Example of increasing entropy
Ice melting provides an example in which entropy increases in a small system, a thermodynamic system consisting of the surroundings (the warm room) and the entity of glass container, ice, water which has been allowed to reach thermodynamic equilibriumThermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
at the melting temperature of ice. In this system, some heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
(δQ) from the warmer surroundings at 298 K (77°F, 25°C) transfers to the cooler system of ice and water at its constant temperature (T) of 273 K (32°F, 0°C), the melting temperature of ice. The entropy of the system, which is δQ/T, increases by δQ/273K. The heat δQ for this process is the energy required to change water from the solid state to the liquid state, and is called the enthalpy of fusion
Enthalpy of fusion
The enthalpy of fusion is the change in enthalpy resulting from heating one mole of a substance to change its state from a solid to a liquid. The temperature at which this occurs is the melting point....
, i.e. ΔH for ice fusion.
It is important to realize that the entropy of the surrounding room decreases less than the entropy of the ice and water increases: the room temperature of 298 K is larger than 273 K and therefore the ratio, (entropy change), of δQ/298K for the surroundings is smaller than the ratio (entropy change), of δQ/273K for the ice and water system. This is always true in spontaneous events in a thermodynamic system and it shows the predictive importance of entropy: the final net entropy after such an event is always greater than was the initial entropy.
As the temperature of the cool water rises to that of the room and the room further cools imperceptibly, the sum of the δQ/T over the continuous range, “at many increments”, in the initially cool to finally warm water can be found by calculus. The entire miniature ‘universe’, i.e. this thermodynamic system, has increased in entropy. Energy has spontaneously become more dispersed and spread out in that ‘universe’ than when the glass of ice + water was introduced and became a 'system' within it.
Origins and uses
Originally, entropy was named to describe the "waste heat," or more accurately, energy losses, from heat engines and other mechanical devices which could never run with 100% efficiency in converting energy into work. Later, the term came to acquire several additional descriptions, as more was understood about the behavior of molecules on the microscopic level. In the late 19th century, the word "disorder" was used by Ludwig BoltzmannLudwig Boltzmann
Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
in developing statistical views of entropy
Entropy (statistical views)
In classical statistical mechanics, the entropy function earlier introduced by Clausius is changed to statistical entropy using probability theory...
using probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
to describe the increased molecular movement on the microscopic level. That was before quantum behavior came to be better understood by Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
and those who followed. Descriptions of thermodynamic (heat) entropy on the microscopic level are found in statistical thermodynamics and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.
For most of the 20th century, textbooks tended to describe entropy as "disorder", following Boltzmann's early conceptualisation of the motional energy of molecules. More recently, there has been a trend in chemistry and physics textbooks to describe entropy in terms of "dispersal of energy". Entropy can also involve the dispersal of particles, which are themselves energetic. Thus there are instances where both particles and energy disperse at different rates when substances are mixed together.
The mathematics developed in statistical thermodynamics were found to be applicable in other disciplines. In particular, information sciences developed the concept of information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
where a constant replaces the temperature which is inherent in thermodynamic entropy.
Heat and entropy
At a microscopic level, kinetic energy of molecules is responsible for the temperature of a substance or a system. “Heat” is the kinetic energy of molecules being transferred: when motional energy is transferred from hotter surroundings to a cooler system, faster moving molecules in the surroundings collide with the walls of the system which transfers some of their energy to the molecules of the system and makes them move faster.- Molecules in a gas like nitrogen at room temperature at any instant are moving at an average speed of nearly 500 miles per hour (210 m/s), repeatedly colliding and therefore exchanging energy so that their individual speeds are always changing, even being motionless for an instant if two molecules with exactly the same speed collide head-on, before another molecule hits them and they race off, as fast as 2500 miles an hour. (At higher temperatures average speeds increase and motional energy becomes proportionately greater.)
- Thus motional molecular energy (‘heat energy’) from hotter surroundings, like faster moving molecules in a flame or violently vibrating iron atoms in a hot plate, will melt or boil a substance (the system) at the temperature of its melting or boiling point. That amount of motional energy from the surroundings that is required for melting or boiling is called the phase change energy, specifically the enthalpy of fusion or of vaporization, respectively. This phase change energy breaks bonds between the molecules in the system (not chemical bonds inside the molecules that hold the atoms together) rather than contributing to the motional energy and making the molecules move any faster – so it doesn’t raise the temperature, but instead enables the molecules to break free to move as a liquid or as a vapor.
- In terms of energy, when a solid becomes a liquid or a liquid a vapor, motional energy coming from the surroundings is changed to ‘ potential energy ‘ in the substance (phase change energy, which is released back to the surroundings when the surroundings become cooler than the substance's boiling or melting temperature, respectively). Phase change energy increases the entropy of a substance or system because it is energy that must be spread out in the system from the surroundings so that the substance can exist as a liquid or vapor at a temperature above its melting or boiling point. When this process occurs in a ‘universe’ that consists of the surroundings plus the system, the total energy of the universe becomes more dispersed or spread out as part of the greater energy that was only in the hotter surroundings transfers so that some is in the cooler system. This energy dispersal increases the entropy of the 'universe'.
The important overall principle is that ”Energy of all types changes from being localized to becoming dispersed or spread out, if it is not hindered from doing so. Entropy (or better, entropy change) is the quantitative measure of that kind of a spontaneous process: how much energy has been transferred/T or how widely it has become spread out at a specific temperature.
Classical calculation of entropy
When entropy was first defined and used in 1865 the very existence of atoms was still controversial and there was no concept that temperature was due to the motional energy of molecules or that “heat” was actually the transferring of that motional molecular energy from one place to another. Entropy change,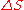 , was described in macroscopic terms that could be directly measured, such as volume, temperature, or pressure. However, today the classical equation of entropy,
, was described in macroscopic terms that could be directly measured, such as volume, temperature, or pressure. However, today the classical equation of entropy, 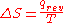 can be explained, part by part, in modern terms describing how molecules are responsible for what is happening:
can be explained, part by part, in modern terms describing how molecules are responsible for what is happening:-
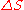 is the change in entropy of a system (some physical substance of interest) after some motional energy (“heat”) has been transferred to it by fast moving molecules. So,
is the change in entropy of a system (some physical substance of interest) after some motional energy (“heat”) has been transferred to it by fast moving molecules. So,  .
.
- Then,
 , the quotient of the motional energy (“heat”) q that is transferred "reversibly" (rev) to the system from the surroundings (or from another system in contact with the first system) divided by T, the absolute temperature at which the transfer occurs.
, the quotient of the motional energy (“heat”) q that is transferred "reversibly" (rev) to the system from the surroundings (or from another system in contact with the first system) divided by T, the absolute temperature at which the transfer occurs.
- “Reversible” or “reversibly” (rev) simply means that T, the temperature of the system, has to stay (almost) exactly the same while any energy is being transferred to or from it. That’s easy in the case of phase changes, where the system absolutely must stay in the solid or liquid form until enough energy is given to it to break bonds between the molecules before it can change to a liquid or a gas. For example in the melting of ice at 273.15 K, no matter what temperature the surroundings are – from 273.20 K to 500 K or even higher, the temperature of the ice will stay at 273.15 K until the last molecules in the ice are changed to liquid water, i.e., until all the hydrogen bonds between the water molecules in ice are broken and new, less-exactly fixed hydrogen bonds between liquid water molecules are formed. This amount of energy necessary for ice melting per mole has been found to be 6008 joules at 273 K. Therefore, the entropy change per mole is
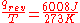 , or 22 J/K.
, or 22 J/K. - When the temperature isn't at the melting or boiling point of a substance no intermolecular bond-breaking is possible, and so any motional molecular energy (“heat”) from the surroundings transferred to a system raises its temperature, making its molecules move faster and faster. As the temperature is constantly rising, there is no longer a particular value of “T” at which energy is transferred. However, a "reversible" energy transfer can be measured at a very small temperature increase, and a cumulative total can be found by adding each of many small temperature intervals or increments. For example, to find the entropy change
 from 300 K to 310 K, measure the amount of energy transferred at dozens or hundreds of temperature increments, say from 300.00 K to 300.01 K and then 300.01 to 300.02 and so on, dividing the q by each T, and finally adding them all.
from 300 K to 310 K, measure the amount of energy transferred at dozens or hundreds of temperature increments, say from 300.00 K to 300.01 K and then 300.01 to 300.02 and so on, dividing the q by each T, and finally adding them all. - Calculus can be used to make this calculation easier if the effect of energy input to the system is linearly dependent on the temperature change, as in simple heating of a system at moderate to relatively high temperatures. Thus, the energy being transferred “per incremental change in temperature” (the heat capacity,
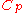 ), multiplied by the integralIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
), multiplied by the integralIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of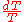 from
from  to
to  , is directly given by
, is directly given by  .
.
- “Reversible” or “reversibly” (rev) simply means that T, the temperature of the system, has to stay (almost) exactly the same while any energy is being transferred to or from it. That’s easy in the case of phase changes, where the system absolutely must stay in the solid or liquid form until enough energy is given to it to break bonds between the molecules before it can change to a liquid or a gas. For example in the melting of ice at 273.15 K, no matter what temperature the surroundings are – from 273.20 K to 500 K or even higher, the temperature of the ice will stay at 273.15 K until the last molecules in the ice are changed to liquid water, i.e., until all the hydrogen bonds between the water molecules in ice are broken and new, less-exactly fixed hydrogen bonds between liquid water molecules are formed. This amount of energy necessary for ice melting per mole has been found to be 6008 joules at 273 K. Therefore, the entropy change per mole is
Introductory descriptions of entropy
Traditionally, 20th century textbooks have introduced entropy as order and disorderEntropy (order and disorder)
In thermodynamics, entropy is commonly associated with the amount of order, disorder, and/or chaos in a thermodynamic system. This stems from Rudolf Clausius' 1862 assertion that any thermodynamic processes always "admits to being reduced to the alteration in some way or another of the arrangement...
so that it provides "a measurement of the disorder or randomness of a system". It has been argued that ambiguities in the terms used (such as "disorder" and "chaos") contribute to widespread confusion and can hinder comprehension of entropy for most students. A more recent formulation associated with Frank L. Lambert
Frank L. Lambert
Frank L. Lambert is a Professor Emeritus of Chemistry at Occidental College, Los Angeles. He is known for his advocacy of changing the definition of thermodynamic entropy as “disorder” in US general chemistry texts to its replacement by viewing entropy as a measure of energy dispersal.-Teaching...
describing entropy as energy dispersal
Entropy (energy dispersal)
The description of entropy as energy dispersal provides an introductory method of teaching the thermodynamic concept of entropy. In physics and physical chemistry, entropy has commonly been defined as a scalar measure of the disorder of a thermodynamic system...
describes entropy as measuring "the spontaneous dispersal of energy — at a specific temperature."
See also
- Entropy (energy dispersal)Entropy (energy dispersal)The description of entropy as energy dispersal provides an introductory method of teaching the thermodynamic concept of entropy. In physics and physical chemistry, entropy has commonly been defined as a scalar measure of the disorder of a thermodynamic system...
- Second law of thermodynamicsSecond law of thermodynamicsThe second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
- Statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
- ThermodynamicsThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
- Application of entropy to drug selectivity
Further reading
- Goldstein, Martin and Inge F. (1993) The Refrigerator and the Universe: Understanding the Laws of Energy. Harvard Univ. Press. Chpts. 4-12 touch on entropy in some way.


