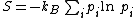Entropy (statistical views)
Encyclopedia
In classical
statistical mechanics
, the entropy
function earlier introduced by Clausius is changed to statistical entropy using probability theory
. The statistical entropy perspective was introduced in 1870 with the work of the Austrian physicist Ludwig Boltzmann
.
that are accessible to a system in the course of its thermal fluctuations
. So the entropy is defined over two different levels of description of the given system. The entropy is given by the Gibbs entropy formula, named after J. Willard Gibbs
. For a classical system (i.e., a collection of classical particles) with a discrete set of microstates, if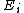
is the energy of microstate i, and 
is its probability that it occurs during the system's fluctuations, then the entropy of the system is
The quantity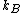
is a physical constant
known as Boltzmann's constant, which, like the entropy, has units of heat capacity
. The logarithm
is dimensionless.
This definition remains valid even when the system is far away from equilibrium. Other definitions assume that the system is in thermal equilibrium
, either as an isolated system
, or as a system in exchange with its surroundings. The set of microstates on which the sum is to be done is called a statistical ensemble. Each statistical ensemble (micro-canonical, canonical, grand-canonical, etc.) describes a different configuration of the system's exchanges with the outside, from an isolated system to a system that can exchange one more quantity with a reservoir, like energy, volume or molecules. In every ensemble, the equilibrium
configuration of the system is dictated by the maximization of the entropy of the union of the system and its reservoir, according to the second law of thermodynamics
(see the statistical mechanics
article).
Neglecting correlation
s between the different possible states (or, more generally, neglecting statistical dependencies
between states) will lead to an overestimate of the entropy. These correlations occur in systems of interacting particles, that is, in all systems more complex than an ideal gas
.
This S is almost universally called simply the entropy. It can also be called the statistical entropy or the thermodynamic entropy without changing the meaning. Note the above expression of the statistical entropy is a discretized version of Shannon entropy. The von Neumann entropy
formula is an extension of the Gibbs entropy formula to the quantum mechanical
case.
, consistent with its macroscopic thermodynamic properties (or macrostate). To understand what microstates and macrostates are, consider the example of a gas
in a container. At a microscopic level, the gas consists of a vast number
of freely moving atom
s, which occasionally collide with one another and with the walls of the container. The microstate of the system is a description of the positions and momenta
of all the atoms. In principle, all the physical properties of the system are determined by its microstate. However, because the number of atoms is so large, the motion of individual atoms is mostly irrelevant to the behavior of the system as a whole. Provided the system is in thermodynamic equilibrium, the system can be adequately described by a handful of macroscopic quantities, called "thermodynamic variables": the total energy
E, volume
V, pressure
P, temperature
T, and so forth. The macrostate of the system is a description of its thermodynamic variables.
There are three important points to note. Firstly, to specify any one microstate, we need to write down an impractically long list of numbers, whereas specifying a macrostate requires only a few numbers (E, V, etc.). However, and this is the second point, the usual thermodynamic equations
only describe the macrostate of a system adequately when this system is in equilibrium; non-equilibrium situations can generally not be described by a small number of variables. For example, if a gas is sloshing around in its container, even a macroscopic description would have to include, e.g., the velocity of the fluid at each different point. Actually, the macroscopic state of the system will be described by a small number of variables only if the system is at global thermodynamic equilibrium
. Thirdly, more than one microstate can correspond to a single macrostate. In fact, for any given macrostate, there will be a huge number of microstates that are consistent with the given values of E, V, etc.
We are now ready to provide a definition of entropy. The entropy S is defined as
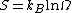
where
The statistical entropy reduces to Boltzmann's entropy when all the accessible microstates of the system are equally likely. It is also the configuration corresponding to the maximum of a system's entropy for a given set of accessible microstates
, in other words the macroscopic configuration in which the lack of information is maximal. As such, according to the second law of thermodynamics
, it is the equilibrium
configuration of an isolated system. Boltzmann's entropy is the expression of entropy at thermodynamic equilibrium in the micro-canonical ensemble.
This postulate, which is known as Boltzmann's principle, may be regarded as the foundation of statistical mechanics
, which describes thermodynamic systems using the statistical behaviour of its constituents. It turns out that S is itself a thermodynamic property, just like E or V. Therefore, it acts as a link between the microscopic world and the macroscopic. One important property of S follows readily from the definition: since Ω is a natural number
(1,2,3,...), S is either zero or positive (ln(1)=0, lnΩ≥0.)
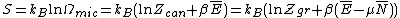
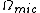is the microcanonical partition function
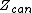is the canonical partition function
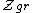is the grand canonical partition function
s, each of which is either heads up or tails up
. The macrostates are specified by the total number of heads and tails, whereas the microstates are specified by the facings of each individual coin. For the macrostates of 100 heads or 100 tails, there is exactly one possible configuration, so our knowledge of the system is complete. At the opposite extreme, the macrostate which gives us the least knowledge about the system consists of 50 heads and 50 tails in any order, for which there are 100,891,344,545,564,193,334,812,497,256 (100 choose 50
) ≈ 1029 possible microstates.
Even when a system is entirely isolated from external influences, its microstate is constantly changing. For instance, the particles in a gas are constantly moving, and thus occupy a different position at each moment of time; their momenta are also constantly changing as they collide with each other or with the container walls. Suppose we prepare the system in an artificially highly-ordered equilibrium state. For instance, imagine dividing a container with a partition and placing a gas on one side of the partition, with a vacuum on the other side. If we remove the partition and watch the subsequent behavior of the gas, we will find that its microstate evolves according to some chaotic and unpredictable pattern, and that on average these microstates will correspond to a more disordered macrostate than before. It is possible, but extremely unlikely, for the gas molecules to bounce off one another in such a way that they remain in one half of the container. It is overwhelmingly probable for the gas to spread out to fill the container evenly, which is the new equilibrium macrostate of the system.
This is an example illustrating the Second Law of Thermodynamics
:
Since its discovery, this idea has been the focus of a great deal of thought, some of it confused. A chief point of confusion is the fact that the Second Law applies only to isolated systems. For example, the Earth
is not an isolated system because it is constantly receiving energy in the form of sunlight
. In contrast, the universe
may be considered an isolated system, so that its total disorder is constantly increasing.
statistical mechanics
, the number of microstates is actually uncountably infinite
, since the properties of classical systems are continuous. For example, a microstate of a classical ideal gas is specified by the positions and momenta of all the atoms, which range continuously over the real number
s. If we want to define Ω, we have to come up with a method of grouping the microstates together to obtain a countable set. This procedure is known as coarse graining. In the case of the ideal gas, we count two states of an atom as the "same" state if their positions and momenta are within δx and δp of each other. Since the values of δx and δp can be chosen arbitrarily, the entropy is not uniquely defined. It is defined only up to an additive constant. (As we will see, the thermodynamic definition of entropy is also defined only up to a constant.)
This ambiguity can be resolved with quantum mechanics
. The quantum state of a system can be expressed as a superposition of "basis" states, which can be chosen to be energy eigenstates (i.e. eigenstates of the quantum Hamiltonian
.) Usually, the quantum states are discrete, even though there may be an infinite number of them. For a system with some specified energy E, one takes Ω to be the number of energy eigenstates within a macroscopically small energy range between E and E + δE. In the thermodynamical limit, the specific entropy becomes independent on the choice of δE.
An important result, known as Nernst's theorem or the third law of thermodynamics
, states that the entropy of a system at zero absolute temperature
is a well-defined constant. This is because a system at zero temperature exists in its lowest-energy state, or ground state
, so that its entropy is determined by the degeneracy
of the ground state. Many systems, such as crystal lattices
, have a unique ground state, and (since ln(1) = 0) this means that they have zero entropy at absolute zero. Other systems have more than one state with the same, lowest energy, and have a non-vanishing "zero-point entropy". For instance, ordinary ice
has a zero-point entropy of 3.41 J/(mol·K), because its underlying crystal structure
possesses multiple configurations with the same energy (a phenomenon known as geometrical frustration
).
The third law of thermodynamics states that the entropy of a perfect crystal at absolute zero, or 0 kelvin
is zero. This means that in a perfect crystal, at 0 kelvin, nearly all molecular motion should cease in order to achieve ΔS=0. A perfect crystal is one in which the internal lattice structure is the same at all times; in other words, it is fixed and non-moving, and does not have rotational or vibrational energy. This means that there is only one way in which this order can be attained: when every particle of the structure is in its proper place.
However, the equation for predicting quantized vibrational levels shows that even when the vibrational quantum number is 0, the molecule still has vibrational energy. This means that no matter how cold the temperature gets, the molecule will always have vibration. This is in keeping with the Heisenberg uncertainty principle, which states that both the position and the momentum of a particle cannot be known precisely, at a given time:
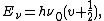
where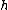
is Planck's constant, 
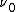is the characteristic frequency of the vibration, and 
is the vibrational quantum number. Note that even when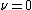 
(the zero-point energy
),
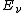does not equal 0.
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
function earlier introduced by Clausius is changed to statistical entropy using probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. The statistical entropy perspective was introduced in 1870 with the work of the Austrian physicist Ludwig Boltzmann
Ludwig Boltzmann
Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
.
Gibbs Entropy Formula
The macroscopic state of the system is defined by a distribution on the microstatesMicrostate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
that are accessible to a system in the course of its thermal fluctuations
Thermal fluctuations
In statistical mechanics, thermal fluctuations are random deviations of a system from its equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they disappear altogether as temperature approaches absolute zero.Thermal fluctuations are a...
. So the entropy is defined over two different levels of description of the given system. The entropy is given by the Gibbs entropy formula, named after J. Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
. For a classical system (i.e., a collection of classical particles) with a discrete set of microstates, if
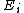is the energy of microstate i, and is its probability that it occurs during the system's fluctuations, then the entropy of the system is
The quantity
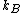is a physical constantPhysical constant
A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
known as Boltzmann's constant, which, like the entropy, has units of heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
. The logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
is dimensionless.
This definition remains valid even when the system is far away from equilibrium. Other definitions assume that the system is in thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
, either as an isolated system
Isolated system
In the natural sciences an isolated system, as contrasted with an open system, is a physical system without any external exchange. If it has any surroundings, it does not interact with them. It obeys in particular the first of the conservation laws: its total energy - mass stays constant...
, or as a system in exchange with its surroundings. The set of microstates on which the sum is to be done is called a statistical ensemble. Each statistical ensemble (micro-canonical, canonical, grand-canonical, etc.) describes a different configuration of the system's exchanges with the outside, from an isolated system to a system that can exchange one more quantity with a reservoir, like energy, volume or molecules. In every ensemble, the equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
configuration of the system is dictated by the maximization of the entropy of the union of the system and its reservoir, according to the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
(see the statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
article).
Neglecting correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
s between the different possible states (or, more generally, neglecting statistical dependencies
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
between states) will lead to an overestimate of the entropy. These correlations occur in systems of interacting particles, that is, in all systems more complex than an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
.
This S is almost universally called simply the entropy. It can also be called the statistical entropy or the thermodynamic entropy without changing the meaning. Note the above expression of the statistical entropy is a discretized version of Shannon entropy. The von Neumann entropy
Von Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
formula is an extension of the Gibbs entropy formula to the quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
case.
Boltzmann's principle
In Boltzmann's definition, entropy is a measure of the number of possible microscopic states (or microstates) of a system in thermodynamic equilibriumThermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, consistent with its macroscopic thermodynamic properties (or macrostate). To understand what microstates and macrostates are, consider the example of a gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
in a container. At a microscopic level, the gas consists of a vast number
Avogadro's number
In chemistry and physics, the Avogadro constant is defined as the ratio of the number of constituent particles N in a sample to the amount of substance n through the relationship NA = N/n. Thus, it is the proportionality factor that relates the molar mass of an entity, i.e...
of freely moving atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s, which occasionally collide with one another and with the walls of the container. The microstate of the system is a description of the positions and momenta
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of all the atoms. In principle, all the physical properties of the system are determined by its microstate. However, because the number of atoms is so large, the motion of individual atoms is mostly irrelevant to the behavior of the system as a whole. Provided the system is in thermodynamic equilibrium, the system can be adequately described by a handful of macroscopic quantities, called "thermodynamic variables": the total energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
E, volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
V, pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
P, temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
T, and so forth. The macrostate of the system is a description of its thermodynamic variables.
There are three important points to note. Firstly, to specify any one microstate, we need to write down an impractically long list of numbers, whereas specifying a macrostate requires only a few numbers (E, V, etc.). However, and this is the second point, the usual thermodynamic equations
Thermodynamic equations
Thermodynamics is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process...
only describe the macrostate of a system adequately when this system is in equilibrium; non-equilibrium situations can generally not be described by a small number of variables. For example, if a gas is sloshing around in its container, even a macroscopic description would have to include, e.g., the velocity of the fluid at each different point. Actually, the macroscopic state of the system will be described by a small number of variables only if the system is at global thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
. Thirdly, more than one microstate can correspond to a single macrostate. In fact, for any given macrostate, there will be a huge number of microstates that are consistent with the given values of E, V, etc.
We are now ready to provide a definition of entropy. The entropy S is defined as
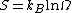
where
- kB is Boltzmann's constant and
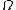is the number of microstates consistent with the given macrostate.
The statistical entropy reduces to Boltzmann's entropy when all the accessible microstates of the system are equally likely. It is also the configuration corresponding to the maximum of a system's entropy for a given set of accessible microstates
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
, in other words the macroscopic configuration in which the lack of information is maximal. As such, according to the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
, it is the equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
configuration of an isolated system. Boltzmann's entropy is the expression of entropy at thermodynamic equilibrium in the micro-canonical ensemble.
This postulate, which is known as Boltzmann's principle, may be regarded as the foundation of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, which describes thermodynamic systems using the statistical behaviour of its constituents. It turns out that S is itself a thermodynamic property, just like E or V. Therefore, it acts as a link between the microscopic world and the macroscopic. One important property of S follows readily from the definition: since Ω is a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
(1,2,3,...), S is either zero or positive (ln(1)=0, lnΩ≥0.)
Ensembles
The various ensembles used in statistical thermodynamics are linked to the entropy by the following relations: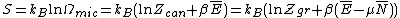 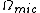is the microcanonical partition functionMicrocanonical ensemble
In statistical physics, the microcanonical ensemble is a theoretical tool used to describe the thermodynamic properties of an isolated system. In such a system, the possible macrostates of the system all have the same energy and the probability for the system to be in any given microstate is the same...
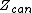is the canonical partition functionCanonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
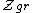is the grand canonical partition functionGrand canonical ensemble
In statistical mechanics, a grand canonical ensemble is a theoretical collection of model systems put together to mirror the calculated probability distribution of microscopic states of a given physical system which is being maintained in a given macroscopic state...
Lack of knowledge and the second law of thermodynamics
We can view Ω as a measure of our lack of knowledge about a system. As an illustration of this idea, consider a set of 100 coinCoin
A coin is a piece of hard material that is standardized in weight, is produced in large quantities in order to facilitate trade, and primarily can be used as a legal tender token for commerce in the designated country, region, or territory....
s, each of which is either heads up or tails up
Coin flipping
Coin flipping or coin tossing or heads or tails is the practice of throwing a coin in the air to choose between two alternatives, sometimes to resolve a dispute between two parties...
. The macrostates are specified by the total number of heads and tails, whereas the microstates are specified by the facings of each individual coin. For the macrostates of 100 heads or 100 tails, there is exactly one possible configuration, so our knowledge of the system is complete. At the opposite extreme, the macrostate which gives us the least knowledge about the system consists of 50 heads and 50 tails in any order, for which there are 100,891,344,545,564,193,334,812,497,256 (100 choose 50
Combination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
) ≈ 1029 possible microstates.
Even when a system is entirely isolated from external influences, its microstate is constantly changing. For instance, the particles in a gas are constantly moving, and thus occupy a different position at each moment of time; their momenta are also constantly changing as they collide with each other or with the container walls. Suppose we prepare the system in an artificially highly-ordered equilibrium state. For instance, imagine dividing a container with a partition and placing a gas on one side of the partition, with a vacuum on the other side. If we remove the partition and watch the subsequent behavior of the gas, we will find that its microstate evolves according to some chaotic and unpredictable pattern, and that on average these microstates will correspond to a more disordered macrostate than before. It is possible, but extremely unlikely, for the gas molecules to bounce off one another in such a way that they remain in one half of the container. It is overwhelmingly probable for the gas to spread out to fill the container evenly, which is the new equilibrium macrostate of the system.
This is an example illustrating the Second Law of Thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
:
- the total entropy of any isolated thermodynamic system tends to increase over time, approaching a maximum value.
Since its discovery, this idea has been the focus of a great deal of thought, some of it confused. A chief point of confusion is the fact that the Second Law applies only to isolated systems. For example, the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is not an isolated system because it is constantly receiving energy in the form of sunlight
Sunlight
Sunlight, in the broad sense, is the total frequency spectrum of electromagnetic radiation given off by the Sun. On Earth, sunlight is filtered through the Earth's atmosphere, and solar radiation is obvious as daylight when the Sun is above the horizon.When the direct solar radiation is not blocked...
. In contrast, the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
may be considered an isolated system, so that its total disorder is constantly increasing.
Counting of microstates
In classicalClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the number of microstates is actually uncountably infinite
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
, since the properties of classical systems are continuous. For example, a microstate of a classical ideal gas is specified by the positions and momenta of all the atoms, which range continuously over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. If we want to define Ω, we have to come up with a method of grouping the microstates together to obtain a countable set. This procedure is known as coarse graining. In the case of the ideal gas, we count two states of an atom as the "same" state if their positions and momenta are within δx and δp of each other. Since the values of δx and δp can be chosen arbitrarily, the entropy is not uniquely defined. It is defined only up to an additive constant. (As we will see, the thermodynamic definition of entropy is also defined only up to a constant.)
This ambiguity can be resolved with quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. The quantum state of a system can be expressed as a superposition of "basis" states, which can be chosen to be energy eigenstates (i.e. eigenstates of the quantum Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
.) Usually, the quantum states are discrete, even though there may be an infinite number of them. For a system with some specified energy E, one takes Ω to be the number of energy eigenstates within a macroscopically small energy range between E and E + δE. In the thermodynamical limit, the specific entropy becomes independent on the choice of δE.
An important result, known as Nernst's theorem or the third law of thermodynamics
Third law of thermodynamics
The third law of thermodynamics is a statistical law of nature regarding entropy:For other materials, the residual entropy is not necessarily zero, although it is always zero for a perfect crystal in which there is only one possible ground state.-History:...
, states that the entropy of a system at zero absolute temperature
Absolute zero
Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
is a well-defined constant. This is because a system at zero temperature exists in its lowest-energy state, or ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
, so that its entropy is determined by the degeneracy
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
of the ground state. Many systems, such as crystal lattices
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
, have a unique ground state, and (since ln(1) = 0) this means that they have zero entropy at absolute zero. Other systems have more than one state with the same, lowest energy, and have a non-vanishing "zero-point entropy". For instance, ordinary ice
Ice
Ice is water frozen into the solid state. Usually ice is the phase known as ice Ih, which is the most abundant of the varying solid phases on the Earth's surface. It can appear transparent or opaque bluish-white color, depending on the presence of impurities or air inclusions...
has a zero-point entropy of 3.41 J/(mol·K), because its underlying crystal structure
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
possesses multiple configurations with the same energy (a phenomenon known as geometrical frustration
Geometrical frustration
In condensed matter physics, the term geometrical frustration means a phenomenon in which the geometrical properties of the crystal lattice or the presence of conflicting atomic forces forbid simultaneous minimization of the interaction energies acting at a given site.This may lead to highly...
).
The third law of thermodynamics states that the entropy of a perfect crystal at absolute zero, or 0 kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
is zero. This means that in a perfect crystal, at 0 kelvin, nearly all molecular motion should cease in order to achieve ΔS=0. A perfect crystal is one in which the internal lattice structure is the same at all times; in other words, it is fixed and non-moving, and does not have rotational or vibrational energy. This means that there is only one way in which this order can be attained: when every particle of the structure is in its proper place.
However, the equation for predicting quantized vibrational levels shows that even when the vibrational quantum number is 0, the molecule still has vibrational energy. This means that no matter how cold the temperature gets, the molecule will always have vibration. This is in keeping with the Heisenberg uncertainty principle, which states that both the position and the momentum of a particle cannot be known precisely, at a given time:
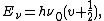
where
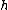is Planck's constant, 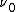is the characteristic frequency of the vibration, and is the vibrational quantum number. Note that even when 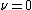(the zero-point energyZero-point energy
Zero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature...
),
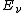does not equal 0.See also
- Boltzmann constant
- Configuration entropyConfiguration entropyIn statistical mechanics, configuration entropy is the portion of a system's entropy that is related to the position of its constituent particles rather than to their velocity or momentum. It is physically related to the number of ways of arranging all the particles of the system while maintaining...
- Conformational entropyConformational entropyConformational entropy is the entropy associated with the physical arrangement of a polymer chain that assumes a compact or globular state in solution. The concept is most commonly applied to biological macromolecules such as proteins and RNA, but can also be used for polysaccharides and other...
- EnthalpyEnthalpyEnthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
- EntropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
- Entropy (classical thermodynamics)
- Entropy (energy dispersal)Entropy (energy dispersal)The description of entropy as energy dispersal provides an introductory method of teaching the thermodynamic concept of entropy. In physics and physical chemistry, entropy has commonly been defined as a scalar measure of the disorder of a thermodynamic system...
- Entropy of mixingEntropy of mixingIn thermodynamics the entropy of mixing is the increase in the total entropy of a compound system, when different and chemically non-reacting chemical substances or material components are mixed by removing partition between the system's initially separate volumes...
- Entropy (order and disorder)Entropy (order and disorder)In thermodynamics, entropy is commonly associated with the amount of order, disorder, and/or chaos in a thermodynamic system. This stems from Rudolf Clausius' 1862 assertion that any thermodynamic processes always "admits to being reduced to the alteration in some way or another of the arrangement...
- History of entropyHistory of entropyThe concept of entropy developed in response to the observation that a certain amount of functional energy released from combustion reactions is always lost to dissipation or friction and is thus not transformed into useful work...
- Information theoryInformation theoryInformation theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
- Thermodynamic free energyThermodynamic free energyThe thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...