Geometrical frustration
Encyclopedia
In condensed matter physics
, the term geometrical frustration (or in short: frustration ) means a phenomenon in which the geometrical properties of the crystal lattice or the presence of conflicting atomic forces forbid simultaneous minimization of the interaction energies acting at a given site.
This may lead to highly degenerate
ground state
s with a nonzero entropy
at zero temperature. Or in simple terms, the substance can never be completely frozen
, because the structure it forms does not have a single minimal-energy state
, so motion on a molecular scale continues even at absolute zero
and even without input of energy
.
The term frustration, in the context of magnetic
systems, is due to Gerard Toulouse (1977) . Frustrated magnetic
systems have been studied for many years. Early work includes a study of the Ising model
on a triangular lattice with nearest-neighbor spin
s coupled antiferromagnetically
by G. H. Wannier
, published in 1950 . Related research on magnets with competing interactions, where
different couplings, each favoring simple (e.g. ferro- and antiferromagnetic), but different structures,
are present. In that case incommensurate
, such as helical
spin arrangements may result, as had been discussed originally by A. Yoshimori, T. A. Kaplan, R. J. Elliott, and others, starting in 1959. A renewed interest in such spin systems with competing or frustrated interactions arose about two decades later in the context of spin glass
es and spatially modulated magnetic superstructures. In spin glasses, frustration is
augmented by stochastic
disorder in the interactions. Well-known spin models with competing or frustrated interactions include the Sherrington-Kirkpatrick model , describing spin glasses, and the ANNNI model
, describing commensurate and incommensurate
magnetic superstructures.
, where it stems from the topological arrangement of spin
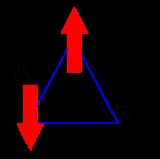
s. A simple 2D example is shown in Figure 1. Three magnetic ions reside on the corners of a triangle with antiferromagnetic
interactions between them—the energy is minimized when each spin is aligned opposite to its neighbors. Once the first two spins align anti-parallel, the third one is frustrated because its two possible orientations, up and down, give the same energy. The third spin cannot simultaneously minimize its interactions with both of the other two. Thus the ground state is twofold degenerate
.
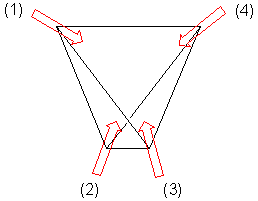
Similarly in three dimensions, four spins arranged in a tetrahedron
(Figure 2) may experience geometric frustration. If there is an antiferromagnetic interaction between spins, then it is not possible to arrange the spins so that all interactions between spins are antiparallel. There are six nearest-neighbor interactions, four of which are antiparallel and thus favourable, but two of which (between 1 and 2, and between 3 and 4) are unfavourable. It is impossible to have all interactions favourable, and the system is frustrated.

Geometrical frustration is also possible if the spins are arranged in a non-collinear
way. If we consider a tetrahedron with a spin on each vertex pointing along the easy axis (that is, directly towards or away from the centre of the tetrahedron), then it is possible to arrange the four spins so that there is no net spin (Figure 3). This is exactly equivalent to having an antiferromagnetic interaction between each pair of spins, so in this case there is no geometrical frustration. With these axes, geometric frustration arises if there is a ferromagnetic interaction between neighbours, where energy is minimized by parallel spins. The best possible arrangement is shown in Figure 4, with two spins pointing towards the centre and two pointing away. The net magnetic moment
points upwards, maximising ferromagnetic interactions in this direction, but left and right vectors cancel out (i.e. are antiferromagnetically aligned), as do forwards and backwards. There are three different equivalent arrangements with two spins out and two in, so the ground state is three-fold degenerate.

in Quantum chromodynamics
): One considers for example expressions ("total energies" or "Hamiltonians") of the form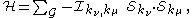
where G is the graph considered, whereas the quantities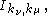 are the so-called „exchange energies“ between nearest-neighbours, which (in the energy units considered) assume the values
are the so-called „exchange energies“ between nearest-neighbours, which (in the energy units considered) assume the values 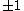 , while the
, while the  are inner products of scalar or vectorial spins or pseudo-spins. If the graph G has quadratic or triangular faces P, the so-called "plaquette variables"
are inner products of scalar or vectorial spins or pseudo-spins. If the graph G has quadratic or triangular faces P, the so-called "plaquette variables" 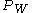 , "loop-products" of the following kind, appear:
, "loop-products" of the following kind, appear: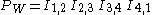 resp.
resp. 
which are also called "frustration products“. One has to perform a sum over these products, summed over all plaquettes. The result for a single plaquette is either +1 or -1. In the last-mentioned case the plaquette is "geometrically frustrated".
It can be shown that the result has a simple gauge invariance: it does not change - nor do so other measurable quantities, e.g. the "total energy" even if locally the exchange integrals and the spins are simultaneously modified as follows:
even if locally the exchange integrals and the spins are simultaneously modified as follows: Here the numbers
Here the numbers 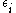 und
und 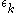 are arbitrary signs, i.e. =+1 or = (-1), so that the modified structure may look totally random.
are arbitrary signs, i.e. =+1 or = (-1), so that the modified structure may look totally random.
 Although most previous and current research on frustration focuses on spin systems, the phenomenon was first studied in ordinary ice
Although most previous and current research on frustration focuses on spin systems, the phenomenon was first studied in ordinary ice
. In 1936 Giauque and Stout published The Entropy of Water and the Third Law of Thermodynamics. Heat Capacity of Ice from 15K to 273K, reporting calorimeter
measurements on water through the freezing and vaporization transitions up to the high temperature gas phase. The entropy
was calculated by integrating the heat capacity
and adding the latent heat
contributions; the low temperature measurements were extrapolated to zero, using Debye’s then recently derived formula . The resulting entropy, S1 = 44.28 cal/(K•mol) = 185.3 J/(mol•K) was compared to the theoretical result from statistical mechanics of an ideal gas, S2 = 45.10 cal/(K•mol) = 188.7 J/(mol•K). The two values differ by S0 = 0.82±0.05 cal/(K•mol) = 3.4 J/(mol•K). This result was then explained by Linus Pauling
, to an excellent approximation, who showed that ice possesses a finite entropy (estimated as 0.81 cal/(K•mol) or 3.4 J/(mol•K)) at zero temperature due to the configurational disorder intrinsic to the protons in ice.
In the hexagonal or cubic
ice phase the oxygen
ions form a tetrahedral structure with an O-O bond length 2.76 Å
(276 pm), while the O-H bond length measures only 0.96 Å (96 pm). Every oxygen (white) ion is surrounded by four hydrogen ions (black) and each hydrogen ion is surrounded by 2 oxygen ions, as shown in Figure 5. Maintaining the internal H2O molecule structure, the minimum energy position of a proton is not half-way between two adjacent oxygen ions. There are two equivalent positions a hydrogen may occupy on the line of the O-O bond, a far and a near position. Thus a rule leads to the frustration of positions of the proton for a ground state configuration: for each oxygen two of the neighboring protons must reside in the far position and two of them in the near position, so-called ‘Ice rules
’. Pauling proposed that the open tetrahedral structure of ice affords many equivalent states satisfying the ice rules.
Pauling went on to compute the configurational entropy in the following way: consider one mole of ice, consisting of N of O2- and 2N of protons. Each O-O bond has two positions for a proton, leading to 22N possible configurations. However, among the 16 possible configurations associated with each oxygen, only 6 are energetically favorable, maintaining the H2O molecule constraint. Then an upper bound of the numbers that the ground state can take is estimated as Ω<22N(6/16)N. Correspondingly the configurational entropy S0 = kBln(Ω) = NkBln(3/2) = 0.81 cal/(K•mol) = 3.4 J/(mol•K) is in amazing agreement with the missing entropy measured by Giauque and Stout.
Although Pauling’s calculation neglected both the global constraint on the number of protons and the local constraint arising from closed loops on the Wurtzite lattice, the estimate was subsequently shown to be of excellent accuracy.
 A mathematically analogous situation to the degeneracy in water ice is found in the spin ice
A mathematically analogous situation to the degeneracy in water ice is found in the spin ice
s. A common spin ice structure is shown in Figure 6 in the cubic pyrochlore structure with one magnetic atom or ion residing on each of the four corners. Due to the strong crystal field
in the material, each of the magnetic ions can be represented by an Ising ground state doublet with a large moment. This suggests a picture of Ising spins residing on the corner-sharing tetrahedral lattice with spins fixed along the local quantization axis, the <111> cubic axes
, which coincide with the lines connecting each tetrahedral vertex to the center. Every tetrahedral cell must have two spins pointing in and two pointing out in order to minimize the energy. Currently the spin ice model has been approximately realized by real materials, most notably the rare earth pyrochlores Ho2Ti2O7, Dy2Ti2O7
, and Ho2Sn2O7. These materials all show nonzero residual entropy at zero kelvins.
(fcc), hexagonal-close-packed, tetrahedron
, pyrochlore
and kagome lattice
s with antiferromagnetic interaction. So frustration is divided into two categories: the first corresponds to the spin glass
, which has both disorder in structure and frustration in spin; the second is the geometrical frustration with an ordered lattice structure and frustration of spin. The frustration of a spin glass is understood within the framework of the RKKY
model, in which the interaction property, either ferromagnetic or anti-ferromagnetic, is dependent on the distance of the two magnetic ions. Due to the lattice disorder in the spin glass, one spin of interest and its nearest neighbors could be at different distances and have a different interaction property, which thus leads to different preferred alignment of the spin.
In 2006 R.F.Wang et al. reported the discovery of an artificial geometrically frustrated magnet composed of arrays of lithographically fabricated single-domain ferromagnetic islands. These islands are manually arranged to create a two-dimensional analog to spin ice. As shown in Figure 7a , to mimic the frustration of spin ice, a two-dimensional analog is created by frustrated arrays consisting of square lattices, in which a single lattice is represented by four ferromagnetic islands meeting at a vertex. For a pair of moments at one vertex, it is favorable to have one pointing in and the other pointing out, while unfavorable to have both pointing out or pointing in, due to energy minimization (Figure 7b). For the four moments at one vertex, there are 16 kinds of configurations, as in Figure 7c. The lowest energy vertex configurations is Type I and II, which have two moments pointing in toward the centre of the vertex, and two pointing out. The percentage of Type I and II are 12.5% and 25% respectively.
Using lithographically fabricated arrays, it is possible to engineer frustrated systems to alter the strength of interactions, the geometry of the lattice, the type and number of defects, and other properties which impact the nature of frustration. The lattice parameters range from 320 nm to 880 nm, with a fixed island size of 80 nm × 220 nm laterally and 25 nm thick, which is small enough for magnetic moments to point lengthwise along the islands and big enough to be stable at 300 K. Figure 8 is AFM (Atomic force microscopy) and MFM (Magnetic force microscopy) images of the frustrated lattice. The black and white halves in Figure 8b indicate the north and south poles of the ferromagnetic island. From the MFM images, the moment configuration of array can be easily determined. The vertex types can be directly observed as described in Figure 7c: the pink vertex is Type I, the green vertex is Type III and the blue vertex is Type II. Thus the artificial spin ice is demonstrated.
In this work on a square lattice of frustrated magnets, Wang et al. observed both ice-like short-range correlations and the absence of long-range correlations, just like in the spin ice at low temperature. These results solidify the uncharted ground on which the real physics of frustration can be visualized and modeled by these artificial geometrically frustrated magnets, and inspires further research activity.
It is sometime possible to establish some local rules, of chemical nature, which lead to low energy configurations and therefore govern structural and chemical order. This is not generally the case and often the local order defined by local interactions cannot propagate freely, leading to geometric frustration. A common feature of all these systems is that, even with simple local rules, they present a large set of, often complex, structural realizations. Geometric frustration plays in role in fields of condensed matter, ranging from clusters and amorphous solids to complex fluids.
The general method of approach to resolve these complications follows two steps. First, the constraint of perfect space-filling is relaxed by allowing for space curvature. An ideal, un-frustrated, structure is defined in this curved space. Then, specific distortions are applied to this ideal template in order to embed it into three dimensional Euclidean space. The final structure is a mixture of ordered regions, where the local order is similar to that of the template, and defects arising from the embedding. Among the possible defects, disclinations play an important role.

Consider first an arrangement of identical discs (a model for a hypothetical two dimensional metal) on a plane; we suppose that the interaction between discs is isotropic and locally tends to arrange the disks in the densest way as possible. The best arrangement for three disks is trivially an equilateral triangle with the disk centers located at the triangle vertices. The study of the long range structure can therefore be reduced to that of plane tilings with equilateral triangles. A well known solution is provided by the triangular tiling with a total compatibility between the local and global rules: the system is said to be ``un-frustrated".
But now, the interaction energy is supposed to be at a minimum when atoms sit on the vertices of a regular pentagon
. Trying to propagate in the long range a packing of these pentagons sharing edges (atomic bonds) and vertices (atoms) is impossible. This is due to the impossibility of tiling a plane with regular pentagons, simply because the pentagon vertex angle does not divide . Three such pentagons can easily fit at a common vertex, but a gap remains between two edges. It is this kind of discrepancy which is called "geometric frustration".
. Three such pentagons can easily fit at a common vertex, but a gap remains between two edges. It is this kind of discrepancy which is called "geometric frustration".
There is one way to overcome this difficulty. Let the surface to be tiled be free of any presupposed topology, and let us build the tiling with a strict application of the local interaction rule. In this simple example, we observe that the surface inherits the topology of a sphere and so receives a curvature. The final structure, here a pentagonal dodecahedron, allows for a perfect propagation of the pentagonal order. It is called an "ideal" (defect-free) model for the considered structure.

A regular tetrahedron is the densest configuration for the packing of four equal spheres. The dense random packing of hard spheres problem can thus be mapped on the tetrahedral packing problem. It is a practical exercise to try to pack table tennis balls in order to form only tetrahedral configurations. One starts with four balls arranged as a perfect tetrahedron, and try to add new spheres, while forming new tetrahedra. The next solution, with five balls, is trivially two tetrahedra sharing a common face; note that already with this solution, the f.c.c. structure, which contains individual tetrahedral holes, does not show such a configuration (the tetrahedra share edges, not faces). With six balls, three regular tetrahedra are built, and the cluster is incompatible with all compact crystalline structures (f.c.c. and h.c.p.). Adding a seventh sphere gives a new cluster consisting in two "axial" balls touching each other and five others touching the latter two balls, the outer shape being an almost regular pentagonal bi-pyramid. However, we are facing now a real packing problem, analogous to the one encountered above with the pentagonal tiling in two dimensions. The dihedral angle of a tetrahedron is not commensurable with ; consequently, a hole remains between two faces of neighboring tetrahedra. As a consequence, a perfect tiling of the Euclidean space R3 is impossible with regular tetrahedra. The frustration has a topological character: it is impossible to fill Euclidean space with tetrahedra, even severely distorted, if we impose that a constant number of tetrahedral (here five) share a common edge.
; consequently, a hole remains between two faces of neighboring tetrahedra. As a consequence, a perfect tiling of the Euclidean space R3 is impossible with regular tetrahedra. The frustration has a topological character: it is impossible to fill Euclidean space with tetrahedra, even severely distorted, if we impose that a constant number of tetrahedral (here five) share a common edge.
The next step is crucial: the search for an un-frustrated structure by allowing for curvature in the space, in order for the local configurations to propagate identically and without defects throughout the whole space.
Regular packing of tetrahedra: the polytope
Twenty tetrahedra pack with a common vertex in such a way that the twelve outer vertices form an irregular icosahedron. Indeed the icosahedron edge length 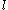 is slightly longer than the circumsphere radius
is slightly longer than the circumsphere radius  (
(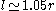 ).
).
There is a solution with regular icosahedra if the space is not Euclidean, but spherical. It is the polytope
 , using the
, using the
Schläffli notation.
There are one hundred and twenty vertices which all belong to the hypersphere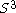 with radius equal to the golden ratio
with radius equal to the golden ratio
 if the edges are of unit length. - The six hundred cells are regular tetrahedra grouped by five around a common edge and by twenty around a common vertex. - This structure is called a polytope (see Coxeter) which is the general name in higher dimension in the series polygon, polyhedron, ... - Even if this structure is embedded in four dimensions, it has been considered as a three dimensional (curved) manifold. This point is conceptually important for the following reason. The ideal models that have been introduced in the curved Space are three dimensional curved templates. They look locally as three dimensional Euclidean models. So, the
if the edges are of unit length. - The six hundred cells are regular tetrahedra grouped by five around a common edge and by twenty around a common vertex. - This structure is called a polytope (see Coxeter) which is the general name in higher dimension in the series polygon, polyhedron, ... - Even if this structure is embedded in four dimensions, it has been considered as a three dimensional (curved) manifold. This point is conceptually important for the following reason. The ideal models that have been introduced in the curved Space are three dimensional curved templates. They look locally as three dimensional Euclidean models. So, the  polytope, which is a tiling by tetrahedra, provides a very dense atomic structure if atoms are located on its vertices. It is therefore naturally used as a template for amorphous metals, but one should not forget that it is at the price of successive idealizations.
polytope, which is a tiling by tetrahedra, provides a very dense atomic structure if atoms are located on its vertices. It is therefore naturally used as a template for amorphous metals, but one should not forget that it is at the price of successive idealizations.
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, the term geometrical frustration (or in short: frustration ) means a phenomenon in which the geometrical properties of the crystal lattice or the presence of conflicting atomic forces forbid simultaneous minimization of the interaction energies acting at a given site.
This may lead to highly degenerate
Degenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
s with a nonzero entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
at zero temperature. Or in simple terms, the substance can never be completely frozen
Freezing
Freezing or solidification is a phase change in which a liquid turns into a solid when its temperature is lowered below its freezing point. The reverse process is melting....
, because the structure it forms does not have a single minimal-energy state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
, so motion on a molecular scale continues even at absolute zero
Absolute zero
Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
and even without input of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
.
The term frustration, in the context of magnetic
Magnetism
Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...
systems, is due to Gerard Toulouse (1977) . Frustrated magnetic
Magnetism
Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...
systems have been studied for many years. Early work includes a study of the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
on a triangular lattice with nearest-neighbor spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
s coupled antiferromagnetically
Antiferromagnetism
In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usuallyrelated to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism...
by G. H. Wannier
Gregory Wannier
Gregory Hugh Wannier was a Swiss physicist.He attended Princeton as a graduate student and later taught at several American universities before a stint in industry....
, published in 1950 . Related research on magnets with competing interactions, where
different couplings, each favoring simple (e.g. ferro- and antiferromagnetic), but different structures,
are present. In that case incommensurate
Commensurability
Two concepts or things are commensurable if they are measurable or comparable by a common standard.Commensurability may refer to:* commensurability , the commensurability of scientific theories...
, such as helical
Helimagnetism
Helimagnetism is an incommensurate form of magnetic ordering that results from the competition between Ferromagnetic and Antiferromagnetic exchange interactions, and is typically only observed at liquid helium temperatures. Spins of neighbouring magnetic moments arrange themselves in a spiral or...
spin arrangements may result, as had been discussed originally by A. Yoshimori, T. A. Kaplan, R. J. Elliott, and others, starting in 1959. A renewed interest in such spin systems with competing or frustrated interactions arose about two decades later in the context of spin glass
Spin glass
A spin glass is a magnet with frustrated interactions, augmented by stochastic disorder, where usually ferromagnetic and antiferromagnetic bonds are randomly distributed...
es and spatially modulated magnetic superstructures. In spin glasses, frustration is
augmented by stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
disorder in the interactions. Well-known spin models with competing or frustrated interactions include the Sherrington-Kirkpatrick model , describing spin glasses, and the ANNNI model
ANNNI model
In statistical physics, the axial next-nearest-neighbor Ising model, usually known as the ANNNI model, is a variant of the Ising model in which competing ferromagnetic and...
, describing commensurate and incommensurate
Commensurability
Two concepts or things are commensurable if they are measurable or comparable by a common standard.Commensurability may refer to:* commensurability , the commensurability of scientific theories...
magnetic superstructures.
Magnetic ordering
Geometrical frustration is an important feature in magnetismMagnetism
Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...
, where it stems from the topological arrangement of spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
s. A simple 2D example is shown in Figure 1. Three magnetic ions reside on the corners of a triangle with antiferromagnetic
Antiferromagnetism
In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usuallyrelated to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism...
interactions between them—the energy is minimized when each spin is aligned opposite to its neighbors. Once the first two spins align anti-parallel, the third one is frustrated because its two possible orientations, up and down, give the same energy. The third spin cannot simultaneously minimize its interactions with both of the other two. Thus the ground state is twofold degenerate
Degenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
.
Similarly in three dimensions, four spins arranged in a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
(Figure 2) may experience geometric frustration. If there is an antiferromagnetic interaction between spins, then it is not possible to arrange the spins so that all interactions between spins are antiparallel. There are six nearest-neighbor interactions, four of which are antiparallel and thus favourable, but two of which (between 1 and 2, and between 3 and 4) are unfavourable. It is impossible to have all interactions favourable, and the system is frustrated.

Geometrical frustration is also possible if the spins are arranged in a non-collinear
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
way. If we consider a tetrahedron with a spin on each vertex pointing along the easy axis (that is, directly towards or away from the centre of the tetrahedron), then it is possible to arrange the four spins so that there is no net spin (Figure 3). This is exactly equivalent to having an antiferromagnetic interaction between each pair of spins, so in this case there is no geometrical frustration. With these axes, geometric frustration arises if there is a ferromagnetic interaction between neighbours, where energy is minimized by parallel spins. The best possible arrangement is shown in Figure 4, with two spins pointing towards the centre and two pointing away. The net magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
points upwards, maximising ferromagnetic interactions in this direction, but left and right vectors cancel out (i.e. are antiferromagnetically aligned), as do forwards and backwards. There are three different equivalent arrangements with two spins out and two in, so the ground state is three-fold degenerate.


Mathematical definition
The mathematical definition is simple (and analogous to the so-called Wilson loopWilson loop
In gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
in Quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
): One considers for example expressions ("total energies" or "Hamiltonians") of the form
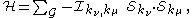
where G is the graph considered, whereas the quantities
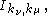 are the so-called „exchange energies“ between nearest-neighbours, which (in the energy units considered) assume the values
are the so-called „exchange energies“ between nearest-neighbours, which (in the energy units considered) assume the values 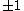 , while the
, while the  are inner products of scalar or vectorial spins or pseudo-spins. If the graph G has quadratic or triangular faces P, the so-called "plaquette variables"
are inner products of scalar or vectorial spins or pseudo-spins. If the graph G has quadratic or triangular faces P, the so-called "plaquette variables" 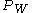 , "loop-products" of the following kind, appear:
, "loop-products" of the following kind, appear: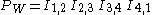 resp.
resp. 
which are also called "frustration products“. One has to perform a sum over these products, summed over all plaquettes. The result for a single plaquette is either +1 or -1. In the last-mentioned case the plaquette is "geometrically frustrated".
It can be shown that the result has a simple gauge invariance: it does not change - nor do so other measurable quantities, e.g. the "total energy"
 even if locally the exchange integrals and the spins are simultaneously modified as follows:
even if locally the exchange integrals and the spins are simultaneously modified as follows: Here the numbers
Here the numbers 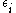 und
und 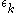 are arbitrary signs, i.e. =+1 or = (-1), so that the modified structure may look totally random.
are arbitrary signs, i.e. =+1 or = (-1), so that the modified structure may look totally random.Water ice

Ice
Ice is water frozen into the solid state. Usually ice is the phase known as ice Ih, which is the most abundant of the varying solid phases on the Earth's surface. It can appear transparent or opaque bluish-white color, depending on the presence of impurities or air inclusions...
. In 1936 Giauque and Stout published The Entropy of Water and the Third Law of Thermodynamics. Heat Capacity of Ice from 15K to 273K, reporting calorimeter
Calorimeter
A calorimeter is a device used for calorimetry, the science of measuring the heat of chemical reactions or physical changes as well as heat capacity. Differential scanning calorimeters, isothermal microcalorimeters, titration calorimeters and accelerated rate calorimeters are among the most common...
measurements on water through the freezing and vaporization transitions up to the high temperature gas phase. The entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
was calculated by integrating the heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
and adding the latent heat
Latent heat
Latent heat is the heat released or absorbed by a chemical substance or a thermodynamic system during a process that occurs without a change in temperature. A typical example is a change of state of matter, meaning a phase transition such as the melting of ice or the boiling of water. The term was...
contributions; the low temperature measurements were extrapolated to zero, using Debye’s then recently derived formula . The resulting entropy, S1 = 44.28 cal/(K•mol) = 185.3 J/(mol•K) was compared to the theoretical result from statistical mechanics of an ideal gas, S2 = 45.10 cal/(K•mol) = 188.7 J/(mol•K). The two values differ by S0 = 0.82±0.05 cal/(K•mol) = 3.4 J/(mol•K). This result was then explained by Linus Pauling
Linus Pauling
Linus Carl Pauling was an American chemist, biochemist, peace activist, author, and educator. He was one of the most influential chemists in history and ranks among the most important scientists of the 20th century...
, to an excellent approximation, who showed that ice possesses a finite entropy (estimated as 0.81 cal/(K•mol) or 3.4 J/(mol•K)) at zero temperature due to the configurational disorder intrinsic to the protons in ice.
In the hexagonal or cubic
Cubic crystal system
In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
ice phase the oxygen
Oxygen
Oxygen is the element with atomic number 8 and represented by the symbol O. Its name derives from the Greek roots ὀξύς and -γενής , because at the time of naming, it was mistakenly thought that all acids required oxygen in their composition...
ions form a tetrahedral structure with an O-O bond length 2.76 Å
Ångström
The angstrom or ångström, is a unit of length equal to 1/10,000,000,000 of a meter . Its symbol is the Swedish letter Å....
(276 pm), while the O-H bond length measures only 0.96 Å (96 pm). Every oxygen (white) ion is surrounded by four hydrogen ions (black) and each hydrogen ion is surrounded by 2 oxygen ions, as shown in Figure 5. Maintaining the internal H2O molecule structure, the minimum energy position of a proton is not half-way between two adjacent oxygen ions. There are two equivalent positions a hydrogen may occupy on the line of the O-O bond, a far and a near position. Thus a rule leads to the frustration of positions of the proton for a ground state configuration: for each oxygen two of the neighboring protons must reside in the far position and two of them in the near position, so-called ‘Ice rules
Ice rules
In chemistry, ice rules are basic principles that govern arrangement of atoms in water ice. They are also known as Bernal–Fowler rules, after British physicists John Desmond Bernal and Ralph H...
’. Pauling proposed that the open tetrahedral structure of ice affords many equivalent states satisfying the ice rules.
Pauling went on to compute the configurational entropy in the following way: consider one mole of ice, consisting of N of O2- and 2N of protons. Each O-O bond has two positions for a proton, leading to 22N possible configurations. However, among the 16 possible configurations associated with each oxygen, only 6 are energetically favorable, maintaining the H2O molecule constraint. Then an upper bound of the numbers that the ground state can take is estimated as Ω<22N(6/16)N. Correspondingly the configurational entropy S0 = kBln(Ω) = NkBln(3/2) = 0.81 cal/(K•mol) = 3.4 J/(mol•K) is in amazing agreement with the missing entropy measured by Giauque and Stout.
Although Pauling’s calculation neglected both the global constraint on the number of protons and the local constraint arising from closed loops on the Wurtzite lattice, the estimate was subsequently shown to be of excellent accuracy.
Spin ice

Spin ice
A spin ice is a substance that is similar to water ice in that it can never be completely frozen. This is because it does not have a single minimal-energy state. A spin ice has "spin" degrees of freedom , with frustrated interactions which prevent it freezing...
s. A common spin ice structure is shown in Figure 6 in the cubic pyrochlore structure with one magnetic atom or ion residing on each of the four corners. Due to the strong crystal field
Crystal field theory
Crystal field theory is a model that describes the electronic structure of transition metal compounds, all of which can be considered coordination complexes. CFT successfully accounts for some magnetic properties, colours, hydration enthalpies, and spinel structures of transition metal complexes,...
in the material, each of the magnetic ions can be represented by an Ising ground state doublet with a large moment. This suggests a picture of Ising spins residing on the corner-sharing tetrahedral lattice with spins fixed along the local quantization axis, the <111> cubic axes
Miller index
Miller indices form a notation system in crystallography for planes and directions in crystal lattices.In particular, a family of lattice planes is determined by three integers h, k, and ℓ, the Miller indices. They are written , and each index denotes a plane orthogonal to a direction in the...
, which coincide with the lines connecting each tetrahedral vertex to the center. Every tetrahedral cell must have two spins pointing in and two pointing out in order to minimize the energy. Currently the spin ice model has been approximately realized by real materials, most notably the rare earth pyrochlores Ho2Ti2O7, Dy2Ti2O7
Dysprosium titanate
Dysprosium titanate is an inorganic compound, a ceramic of the titanate family, with pyrochlore structure. Its CAS number is .Dysprosium titanate, like holmium titanate and holmium stannate, is a spin ice material...
, and Ho2Sn2O7. These materials all show nonzero residual entropy at zero kelvins.
Extension of Pauling’s model: General frustration
The spin ice model is only one subdivision of frustrated systems. The word frustration was initially introduced to describe a system’s inability to simultaneously minimize the competing interaction energy between its components. In general frustration is caused either by competing interactions due to site disorder (see also the Villain model or by lattice structure such as in the triangular, face-centered cubicCubic crystal system
In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
(fcc), hexagonal-close-packed, tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, pyrochlore
Pyrochlore
Pyrochlore 2Nb2O6 is a solid solution between the niobium end member , and the tantalum end member .-Occurrence:...
and kagome lattice
Kagome lattice
A kagome lattice is an arrangement of laths composed of interlaced triangles such that each point where two laths cross has four neighboring points...
s with antiferromagnetic interaction. So frustration is divided into two categories: the first corresponds to the spin glass
Spin glass
A spin glass is a magnet with frustrated interactions, augmented by stochastic disorder, where usually ferromagnetic and antiferromagnetic bonds are randomly distributed...
, which has both disorder in structure and frustration in spin; the second is the geometrical frustration with an ordered lattice structure and frustration of spin. The frustration of a spin glass is understood within the framework of the RKKY
RKKY
RKKY stands for Ruderman-Kittel-Kasuya-Yosida and refers to a coupling mechanism of nuclear magnetic moments or localized inner d or f shell electron spins in a metal by means of an interaction through the conduction electrons....
model, in which the interaction property, either ferromagnetic or anti-ferromagnetic, is dependent on the distance of the two magnetic ions. Due to the lattice disorder in the spin glass, one spin of interest and its nearest neighbors could be at different distances and have a different interaction property, which thus leads to different preferred alignment of the spin.
Artificial geometrically frustrated ferromagnets
Although many properties of spin ice materials have been studied experimentally, little has been revealed about the local accommodation of spin to frustration within the system, since that individual spins cannot be probed without altering the state of the system. Fortunately, with the help of new nanometer techniques, it is possible to fabricate nanometer size magnetic islands analogous to those of the naturally occurring spin ice materials, and they can be probed without altering the moment configuration.In 2006 R.F.Wang et al. reported the discovery of an artificial geometrically frustrated magnet composed of arrays of lithographically fabricated single-domain ferromagnetic islands. These islands are manually arranged to create a two-dimensional analog to spin ice. As shown in Figure 7a , to mimic the frustration of spin ice, a two-dimensional analog is created by frustrated arrays consisting of square lattices, in which a single lattice is represented by four ferromagnetic islands meeting at a vertex. For a pair of moments at one vertex, it is favorable to have one pointing in and the other pointing out, while unfavorable to have both pointing out or pointing in, due to energy minimization (Figure 7b). For the four moments at one vertex, there are 16 kinds of configurations, as in Figure 7c. The lowest energy vertex configurations is Type I and II, which have two moments pointing in toward the centre of the vertex, and two pointing out. The percentage of Type I and II are 12.5% and 25% respectively.
Using lithographically fabricated arrays, it is possible to engineer frustrated systems to alter the strength of interactions, the geometry of the lattice, the type and number of defects, and other properties which impact the nature of frustration. The lattice parameters range from 320 nm to 880 nm, with a fixed island size of 80 nm × 220 nm laterally and 25 nm thick, which is small enough for magnetic moments to point lengthwise along the islands and big enough to be stable at 300 K. Figure 8 is AFM (Atomic force microscopy) and MFM (Magnetic force microscopy) images of the frustrated lattice. The black and white halves in Figure 8b indicate the north and south poles of the ferromagnetic island. From the MFM images, the moment configuration of array can be easily determined. The vertex types can be directly observed as described in Figure 7c: the pink vertex is Type I, the green vertex is Type III and the blue vertex is Type II. Thus the artificial spin ice is demonstrated.
In this work on a square lattice of frustrated magnets, Wang et al. observed both ice-like short-range correlations and the absence of long-range correlations, just like in the spin ice at low temperature. These results solidify the uncharted ground on which the real physics of frustration can be visualized and modeled by these artificial geometrically frustrated magnets, and inspires further research activity.
Geometric Frustration without Lattice
Another type of geometrical frustration arises from the propagation of a local order. A main question that a condensed matter physicist faces is to explain the stability of a solid.It is sometime possible to establish some local rules, of chemical nature, which lead to low energy configurations and therefore govern structural and chemical order. This is not generally the case and often the local order defined by local interactions cannot propagate freely, leading to geometric frustration. A common feature of all these systems is that, even with simple local rules, they present a large set of, often complex, structural realizations. Geometric frustration plays in role in fields of condensed matter, ranging from clusters and amorphous solids to complex fluids.
The general method of approach to resolve these complications follows two steps. First, the constraint of perfect space-filling is relaxed by allowing for space curvature. An ideal, un-frustrated, structure is defined in this curved space. Then, specific distortions are applied to this ideal template in order to embed it into three dimensional Euclidean space. The final structure is a mixture of ordered regions, where the local order is similar to that of the template, and defects arising from the embedding. Among the possible defects, disclinations play an important role.

Simple two-dimensional examples
Two dimensional examples are helpful in order to get some understanding about the origin of the competition between local rules and geometry in the large.Consider first an arrangement of identical discs (a model for a hypothetical two dimensional metal) on a plane; we suppose that the interaction between discs is isotropic and locally tends to arrange the disks in the densest way as possible. The best arrangement for three disks is trivially an equilateral triangle with the disk centers located at the triangle vertices. The study of the long range structure can therefore be reduced to that of plane tilings with equilateral triangles. A well known solution is provided by the triangular tiling with a total compatibility between the local and global rules: the system is said to be ``un-frustrated".
But now, the interaction energy is supposed to be at a minimum when atoms sit on the vertices of a regular pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
. Trying to propagate in the long range a packing of these pentagons sharing edges (atomic bonds) and vertices (atoms) is impossible. This is due to the impossibility of tiling a plane with regular pentagons, simply because the pentagon vertex angle does not divide
 . Three such pentagons can easily fit at a common vertex, but a gap remains between two edges. It is this kind of discrepancy which is called "geometric frustration".
. Three such pentagons can easily fit at a common vertex, but a gap remains between two edges. It is this kind of discrepancy which is called "geometric frustration".There is one way to overcome this difficulty. Let the surface to be tiled be free of any presupposed topology, and let us build the tiling with a strict application of the local interaction rule. In this simple example, we observe that the surface inherits the topology of a sphere and so receives a curvature. The final structure, here a pentagonal dodecahedron, allows for a perfect propagation of the pentagonal order. It is called an "ideal" (defect-free) model for the considered structure.
Dense structures and tetrahedral packings
The stability of metals is a longstanding question of solid state physics, which can only be understood in the quantum mechanical framework by properly taking into account the interaction between the positively charged ions and the valence and conduction electrons. It is nevertheless possible to use a very simplified picture of metallic bonding and only keeps an isotropic type of interactions, leading to structures which can be represented as densely packed spheres. And indeed the crystalline simple metal structures are often either close packed face centered cubic (f.c.c.) or hexagonal close packing (h.c.p.) lattices. Up to some extend amorphous metals and quasicrystals can also be modeled by close packing of spheres. The local atomic order is well modeled by a close packing of tetrahedra, leading to an imperfect icosahedral order.
A regular tetrahedron is the densest configuration for the packing of four equal spheres. The dense random packing of hard spheres problem can thus be mapped on the tetrahedral packing problem. It is a practical exercise to try to pack table tennis balls in order to form only tetrahedral configurations. One starts with four balls arranged as a perfect tetrahedron, and try to add new spheres, while forming new tetrahedra. The next solution, with five balls, is trivially two tetrahedra sharing a common face; note that already with this solution, the f.c.c. structure, which contains individual tetrahedral holes, does not show such a configuration (the tetrahedra share edges, not faces). With six balls, three regular tetrahedra are built, and the cluster is incompatible with all compact crystalline structures (f.c.c. and h.c.p.). Adding a seventh sphere gives a new cluster consisting in two "axial" balls touching each other and five others touching the latter two balls, the outer shape being an almost regular pentagonal bi-pyramid. However, we are facing now a real packing problem, analogous to the one encountered above with the pentagonal tiling in two dimensions. The dihedral angle of a tetrahedron is not commensurable with
 ; consequently, a hole remains between two faces of neighboring tetrahedra. As a consequence, a perfect tiling of the Euclidean space R3 is impossible with regular tetrahedra. The frustration has a topological character: it is impossible to fill Euclidean space with tetrahedra, even severely distorted, if we impose that a constant number of tetrahedral (here five) share a common edge.
; consequently, a hole remains between two faces of neighboring tetrahedra. As a consequence, a perfect tiling of the Euclidean space R3 is impossible with regular tetrahedra. The frustration has a topological character: it is impossible to fill Euclidean space with tetrahedra, even severely distorted, if we impose that a constant number of tetrahedral (here five) share a common edge.The next step is crucial: the search for an un-frustrated structure by allowing for curvature in the space, in order for the local configurations to propagate identically and without defects throughout the whole space.
Regular packing of tetrahedra: the polytope 
Twenty tetrahedra pack with a common vertex in such a way that the twelve outer vertices form an irregular icosahedron. Indeed the icosahedron edge length 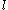 is slightly longer than the circumsphere radius
is slightly longer than the circumsphere radius  (
(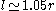 ).
). There is a solution with regular icosahedra if the space is not Euclidean, but spherical. It is the polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
 , using the
, using theSchläffli notation.
There are one hundred and twenty vertices which all belong to the hypersphere
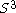 with radius equal to the golden ratio
with radius equal to the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
 if the edges are of unit length. - The six hundred cells are regular tetrahedra grouped by five around a common edge and by twenty around a common vertex. - This structure is called a polytope (see Coxeter) which is the general name in higher dimension in the series polygon, polyhedron, ... - Even if this structure is embedded in four dimensions, it has been considered as a three dimensional (curved) manifold. This point is conceptually important for the following reason. The ideal models that have been introduced in the curved Space are three dimensional curved templates. They look locally as three dimensional Euclidean models. So, the
if the edges are of unit length. - The six hundred cells are regular tetrahedra grouped by five around a common edge and by twenty around a common vertex. - This structure is called a polytope (see Coxeter) which is the general name in higher dimension in the series polygon, polyhedron, ... - Even if this structure is embedded in four dimensions, it has been considered as a three dimensional (curved) manifold. This point is conceptually important for the following reason. The ideal models that have been introduced in the curved Space are three dimensional curved templates. They look locally as three dimensional Euclidean models. So, the  polytope, which is a tiling by tetrahedra, provides a very dense atomic structure if atoms are located on its vertices. It is therefore naturally used as a template for amorphous metals, but one should not forget that it is at the price of successive idealizations.
polytope, which is a tiling by tetrahedra, provides a very dense atomic structure if atoms are located on its vertices. It is therefore naturally used as a template for amorphous metals, but one should not forget that it is at the price of successive idealizations.Literature
- J.F. Sadoc and R. Mosseri, Geometrical Frustration, Cambridge Univ. Press; 1999, reedited 2007
- Sadoc JF, editor. Geometry in condensed matter physics, Singapore, World Scientific; 1990.
- H.S.M. Coxeter, Regular polytopes, Dover pub.; 1973.

