Invariance mechanics
Encyclopedia
In physics, invariance mechanics, in its simplest form, is the rewriting of the laws of quantum field theory
in terms of invariant
quantities only. For example, the positions of a set of particles in a particular coordinate system
is not invariant under translations of the system. However, the (4-dimensional) distances between the particles is invariant under translations
, rotations and Lorentz transformations of the system.
The invariant quantities made from the input and output states of a system are the only quantities needed to give a probability amplitude
to a given system. This is what is meant by the system obeying a symmetry
. Since all the quantities involved are relative
quantities, invariance mechanics, can be thought of as taking relativity theory to its natural limit.
Invariance mechanics has strong links with loop quantum gravity
in which the invariant quantities are based on angular momentum
. In invariance mechanics, space
and time
come secondary to the invariants and are seen as useful concepts that emerge only in the large scale limit.
, vector or spinor
. The rules often involve geometric quantities such as the volumes of simplices formed from vertices of the Feynman graphs.
) and ending points (
) of the particle paths. These points form a complete graph
:
The invariants are the numbers
)
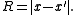
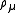There are four invariants on each line:
).
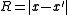
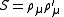
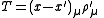
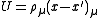
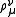There are three invariants on each line: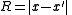
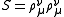
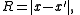
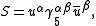
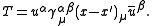
So for example, the fermion propagator is defined in relation to the massless scalar propagator as
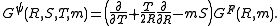
are often used which enables one to decompose a null-vector into a pair of spinors. Alternatively 3-point invariants can be introduced such as the spinor-spinor-vector triangle invariant:
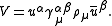
It is important to note that some types of invariants are combinations of other types invariants, for example the angles in a complete-graph are invariants but they can be found as combinations of distance invariants.
In chromodynamics, for example, there are 4-point invariants also. So for a completely specified system you would have several numbers assigned to each line, triangle and tetrahedron in a complete graph representing the system.
One outstanding problem is that of enumerating all the possible invariants which can be made from the various spin and polarisation vectors.
contains many invariant quantities. For large graphs, however, not all these quantities are independent and we must specify dimensional and gauge constraints. Why the particular number of dimensions or particular gauge group is chosen is still not known. The constraints and whether they are satisfied exactly or approximately is the key to invariance mechanics and the difference between it and conventional field theory. Work is being done to see whether the breaking of these constraints is a consequence of the gravitational field. If the constraints are satisfied only approximately, i.e. if there is a quantum uncertainty in the constraints then they are best thought of as local maxima of the amplitudes of a system which occur due to the specific Feynman rules used.
, as specifying that the volume of any (D + 2)-simplex made from the points in the system is zero. The volume of a simplex is given by a formula involving the invariant distances (the R's) between the points which is given by the Cayley–Menger determinants. If this determinant is exactly 0 for all simplices then the geometry is Euclidean
. If the determinant is only approximately 0 then at small distances space-time is non-Euclidean. This has deep connections with quantum foam
and loop quantum gravity
.
For Minkowski space, or for any space with signature (+ + + ... + − ) this makes no difference to the formulae for invariance mechanics.
with reciprocal
functions in the equations), the geometry is no longer confined to flat space-time, this break from flat space-time can be seen as a curvature and, just as in General Relativity
can be seen as the cause of gravity. This is called 'off-dimension' physics in analogy to off-shell physics.
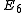involves less invariants than a non-simple gauge group such as U(1)xSU(2)xSU(3) (see: Standard Model
). There has been recent work on combining the dimensional and gauge constraints into a single equation to produce a unified theory. It is thought that this will be achieved by combining of the invariants on each line into a single complex number
(or hypercomplex number
).
. The mixing of space-time and flavour symmetries adds an additional degree of freedom to a particle's light-cone which appears as a unique mass for each particle depending on the flavour.
Having a small number of invariants doesn't necessarily make a simpler model since all the complexity of the model is bound up in the constraints which can be polynomials of hundreds of variables. One of the primary aims of invariance mechanics is to find these polynomial(s) and to find which symmetry group they correspond to. Many believe that the permutation of the variables of these polynomial(s) will correspond to one of the special sporadic groups. (Interestingly, only the largest sporadic group, the monster group
is big enough to incorporate the constraints for the Standard Model
). The other main aim is to find appropriate Feynman rules on the invariants which both accurately describe nature and don't lead to infinities.
have emerged. The argument is that the smallest simplex which needs a constraint to be 4-dimensional is the 6-simplex. This can be viewed as the endpoints of a 3-simplex (a triangular membrane) moving through time. The propagator function of this would be
which is the inverse of the volume of a 6-simplex. In other words the greatest probability would be when the volume of this 6-simplex is 0 and hence it is embedded in 4 dimensions. Hence the propagator for a particle would the same as the dimensional constraint. So if the Universe is built out of 6 simplices then the dimensional constraint can be applied to all simplices. Other fields of work are investigating whether the distance invariants may take only discrete values and whether areas or volumes should be taken as the fundamental invariants. (The dual of loop quantum gravity involves quantized areas).
Others take the view that in invariance mechanics it should be irrelevant whether you view the fundamental constituents as particles or strings or membranes and a more formal approach is called for.
in special relativity
(1905), Yang–Mills gauge invariants theory. Roger Penrose
and his spin-networks (1960's) influenced the subject. Cayley–Menger and their invariant based metric theory was an important milestone. Recently Baratin–Freidel (2006) have demonstrated the connection between invariance mechanics and loop quantum gravity.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
in terms of invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
quantities only. For example, the positions of a set of particles in a particular coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
is not invariant under translations of the system. However, the (4-dimensional) distances between the particles is invariant under translations
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
, rotations and Lorentz transformations of the system.
The invariant quantities made from the input and output states of a system are the only quantities needed to give a probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
to a given system. This is what is meant by the system obeying a symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. Since all the quantities involved are relative
Relative
-General use:*Kinship, the principle binding the most basic social units society. If two people are connected by circumstances of birth, they are said to be relatives-Philosophy:...
quantities, invariance mechanics, can be thought of as taking relativity theory to its natural limit.
Invariance mechanics has strong links with loop quantum gravity
Loop quantum gravity
Loop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
in which the invariant quantities are based on angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. In invariance mechanics, space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
come secondary to the invariants and are seen as useful concepts that emerge only in the large scale limit.
Feynman rules
The Feynman rules of a quantum system can be rewritten in terms of invariant quantities (plus constants such as mass, charge, etc.) The invariant quantities depend on the type of particle, scalarScalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
, vector or spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
. The rules often involve geometric quantities such as the volumes of simplices formed from vertices of the Feynman graphs.
Scalar particles
In a system of scalar particles, the only invariant quantities are the 4-dimensional distances (intervals) between the starting points () and ending points () of the particle paths. These points form a complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
:
The invariants are the numbers
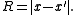
Vector particles
In a system of vector particles such as photons, the invariants are the 4-dimensional distances between the starting points and ending points of the particle paths, and the angles between the starting and ending polarisation vectors of the photons (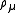 )There are four invariants on each line:
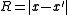
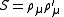
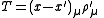
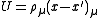
Yang–Mills vector particles
Yang–Mills vector fields of a given gauge group also involve the angle representing a rotation of the gauge group (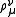 ).There are three invariants on each line:
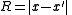
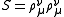
Spinor fields
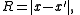
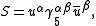
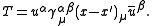
These involve the angles between the spinor vectors. The invariants are:So for example, the fermion propagator is defined in relation to the massless scalar propagator as
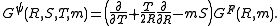
Mixed systems
Systems usually consist of a mixture of scalar, spinor and vector fields and the invariants can depend on angles between spinors and vectors. To simplify this process ideas from twistor theoryTwistor theory
In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...
are often used which enables one to decompose a null-vector into a pair of spinors. Alternatively 3-point invariants can be introduced such as the spinor-spinor-vector triangle invariant:
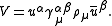
It is important to note that some types of invariants are combinations of other types invariants, for example the angles in a complete-graph are invariants but they can be found as combinations of distance invariants.
In chromodynamics, for example, there are 4-point invariants also. So for a completely specified system you would have several numbers assigned to each line, triangle and tetrahedron in a complete graph representing the system.
One outstanding problem is that of enumerating all the possible invariants which can be made from the various spin and polarisation vectors.
Constraints
A system represented by a complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
contains many invariant quantities. For large graphs, however, not all these quantities are independent and we must specify dimensional and gauge constraints. Why the particular number of dimensions or particular gauge group is chosen is still not known. The constraints and whether they are satisfied exactly or approximately is the key to invariance mechanics and the difference between it and conventional field theory. Work is being done to see whether the breaking of these constraints is a consequence of the gravitational field. If the constraints are satisfied only approximately, i.e. if there is a quantum uncertainty in the constraints then they are best thought of as local maxima of the amplitudes of a system which occur due to the specific Feynman rules used.
Dimensions
Since invariance mechanics does not explicitly use coordinate systems, the definition of dimension is slightly different. The equivalent way of expressing the number of dimensions is given, as in distance geometryDistance geometry
Distance geometry is the characterization and study of sets of points based only on given values of the distances between member pairs. Therefore distance geometry has immediate relevance where distance values are determined or considered, such as in surveying, cartography and...
, as specifying that the volume of any (D + 2)-simplex made from the points in the system is zero. The volume of a simplex is given by a formula involving the invariant distances (the R's) between the points which is given by the Cayley–Menger determinants. If this determinant is exactly 0 for all simplices then the geometry is Euclidean
Euclidean
Euclidean relates to Euclid , a town or others. It may refer to:Geometry...
. If the determinant is only approximately 0 then at small distances space-time is non-Euclidean. This has deep connections with quantum foam
Quantum foam
Quantum foam, also referred to as spacetime foam, is a concept in quantum mechanics, devised by John Wheeler in 1955. The foam is supposed to be the foundations of the fabric of the universe. Additionally, it can be used as a qualitative description of subatomic spacetime turbulence at extremely...
and loop quantum gravity
Loop quantum gravity
Loop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
.
For Minkowski space, or for any space with signature (+ + + ... + − ) this makes no difference to the formulae for invariance mechanics.
Gravity
By allowing quantum uncertainty in the dimensional constraints (which involves replacing delta functionsDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
with reciprocal
Reciprocal
-In mathematics:*Multiplicative inverse, in mathematics, the number 1/x, which multiplied by x gives the product 1, also known as a reciprocal*Reciprocal rule, a technique in calculus for calculating derivatives of reciprocal functions...
functions in the equations), the geometry is no longer confined to flat space-time, this break from flat space-time can be seen as a curvature and, just as in General Relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
can be seen as the cause of gravity. This is called 'off-dimension' physics in analogy to off-shell physics.
Gauge group
In a similar way to expressing the number of dimensions, the dimension and type of the gauge group is given by an identity involving the polarisation (or spin) invariants (the S, T and U's). In the simple cases such as for the photon, these are simply spherical versions of the Cayley–Menger determinants. The gauge group is an internal symmetry because the gauge identity involves far more quantities than the dimensional identity. A simple gauge group such as SU(5) or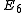 involves less invariants than a non-simple gauge group such as U(1)xSU(2)xSU(3) (see: Standard ModelStandard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
). There has been recent work on combining the dimensional and gauge constraints into a single equation to produce a unified theory. It is thought that this will be achieved by combining of the invariants on each line into a single complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
(or hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
).
Supersymmetry
In the supersymmetric model, some of the spinor invariants and vector invariants are combined together into a single invariant. Having less invariants means that there is more symmetry and more transformations are possible such as transformations between fermions and bosons. It is believed, although currently unproved, that the minimum number of invariants on each line of a complete graph representing a system is two – those being the 4-dimesional distances (the R's) and an angle representing the rotation from one particle 'flavour' to another particle 'flavour' (the T's). Some have suggested that even these invariants can be combined into one by saying that the 4 dimensions of space and time are just 4 more flavours that a particle can have, albeit ones which can change very little (compared with the size of the Universe as a whole). Models of this type imply that the universe has an overall spherical geometrySpherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
. The mixing of space-time and flavour symmetries adds an additional degree of freedom to a particle's light-cone which appears as a unique mass for each particle depending on the flavour.
Having a small number of invariants doesn't necessarily make a simpler model since all the complexity of the model is bound up in the constraints which can be polynomials of hundreds of variables. One of the primary aims of invariance mechanics is to find these polynomial(s) and to find which symmetry group they correspond to. Many believe that the permutation of the variables of these polynomial(s) will correspond to one of the special sporadic groups. (Interestingly, only the largest sporadic group, the monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
is big enough to incorporate the constraints for the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
). The other main aim is to find appropriate Feynman rules on the invariants which both accurately describe nature and don't lead to infinities.
M-theory
Although invariance mechanics was born out of trying to understand point particle theory, possible connections with superstring and M-theoryM-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
have emerged. The argument is that the smallest simplex which needs a constraint to be 4-dimensional is the 6-simplex. This can be viewed as the endpoints of a 3-simplex (a triangular membrane) moving through time. The propagator function of this would be
which is the inverse of the volume of a 6-simplex. In other words the greatest probability would be when the volume of this 6-simplex is 0 and hence it is embedded in 4 dimensions. Hence the propagator for a particle would the same as the dimensional constraint. So if the Universe is built out of 6 simplices then the dimensional constraint can be applied to all simplices. Other fields of work are investigating whether the distance invariants may take only discrete values and whether areas or volumes should be taken as the fundamental invariants. (The dual of loop quantum gravity involves quantized areas).Others take the view that in invariance mechanics it should be irrelevant whether you view the fundamental constituents as particles or strings or membranes and a more formal approach is called for.
History
The history of invariance mechanics is difficult to pinpoint since many people have been working on it without realizing that they were working on invariance mechanics. Notable milestones include the 4-dimensional invariant found by Henri PoincaréHenri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
(1905), Yang–Mills gauge invariants theory. Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
and his spin-networks (1960's) influenced the subject. Cayley–Menger and their invariant based metric theory was an important milestone. Recently Baratin–Freidel (2006) have demonstrated the connection between invariance mechanics and loop quantum gravity.