
Inversion transformation
Encyclopedia
In mathematical physics, inversion transformations are a natural extension of Poincaré transformations to include all conformal
one-to-one transformations on coordinate space-time. They are less studied in physics because unlike the rotations and translations of Poincaré symmetry an object cannot be physically transformed by the inversion symmetry. Some physical theories are invariant under this symmetry, in these cases it is what is known as a 'hidden symmetry'. Other hidden symmetries of physics include gauge symmetry and general covariance
.
began to publish on transformations of the plane generated by inversion in a circle of radius R. His work initiated a large body of publications, now called inversive geometry. The most prominently named mathematician became August Ferdinand Möbius
once he reduced the planar transformations to complex number
arithmetic. In the company of physicists employing the inversion transformation early on was Lord Kelvin, and the association with him leads it to be called the Kelvin transform
.
 ) so that space-time is Euclidean and the equations are simpler. The Poincaré transformations are given by the coordinate transformation on space-time parametrized by the 4-vectors V
) so that space-time is Euclidean and the equations are simpler. The Poincaré transformations are given by the coordinate transformation on space-time parametrized by the 4-vectors V
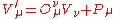
where is an orthogonal matrix
is an orthogonal matrix
and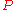 is a 4-vector. Applying this transformation twice on a 4-vector gives a third transformation of the same form. The basic invariant under this transformation is the space-time length given by the distance between two space-time points given by 4-vectors x and y:
is a 4-vector. Applying this transformation twice on a 4-vector gives a third transformation of the same form. The basic invariant under this transformation is the space-time length given by the distance between two space-time points given by 4-vectors x and y:
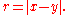
These transformations are subgroups of general 1-1 conformal transformations on space-time. It is possible to extend these transformations to include all 1-1 conformal transformations on space-time
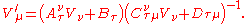
We must also have an equivalent condition to the orthogonality condition of the Poincaré transformations:
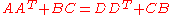
Because one can divide the top and bottom of the transformation by we lose no generality by setting
we lose no generality by setting  to the unit matrix. We end up with
to the unit matrix. We end up with
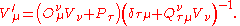
Applying this transformation twice on a 4-vector gives a transformation of the same form. The new symmetry of 'inversion' is given by the 3-tensor This symmetry becomes Poincaré symmetry if we set
This symmetry becomes Poincaré symmetry if we set  When
When  the second condition requires that
the second condition requires that  is an orthogonal matrix. This transformation is 1-1 meaning that each point is mapped to a unique point only if we theoretically include the points at infinity.
is an orthogonal matrix. This transformation is 1-1 meaning that each point is mapped to a unique point only if we theoretically include the points at infinity.
from Möbius transformations:
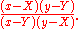
Because the only invariants under this symmetry involve a minimum of 4 points, this symmetry cannot be a symmetry of point particle theory. Point particle theory relies on knowing the lengths of paths of particles through space-time (e.g., from to
to 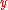 ). The symmetry can be a symmetry of a string theory
). The symmetry can be a symmetry of a string theory
in which the strings are uniquely determined by their endpoints. The propagator
for this theory for a string starting at the endpoints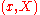 and ending at the endpoints
and ending at the endpoints 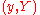 is a conformal function of the 4-dimensional invariant. A string field in endpoint-string theory is a function over the endpoints.
is a conformal function of the 4-dimensional invariant. A string field in endpoint-string theory is a function over the endpoints.
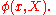
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
one-to-one transformations on coordinate space-time. They are less studied in physics because unlike the rotations and translations of Poincaré symmetry an object cannot be physically transformed by the inversion symmetry. Some physical theories are invariant under this symmetry, in these cases it is what is known as a 'hidden symmetry'. Other hidden symmetries of physics include gauge symmetry and general covariance
General covariance
In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
.
Early use
In 1831 the mathematician Ludwig Immanuel MagnusLudwig Immanuel Magnus
Ludwig Immanuel Magnus was a German Jewish mathematician who, in 1831, published a paper about the inversion transformation, which leads to inversive geometry....
began to publish on transformations of the plane generated by inversion in a circle of radius R. His work initiated a large body of publications, now called inversive geometry. The most prominently named mathematician became August Ferdinand Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
once he reduced the planar transformations to complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
arithmetic. In the company of physicists employing the inversion transformation early on was Lord Kelvin, and the association with him leads it to be called the Kelvin transform
Kelvin transform
The Kelvin transform is a device used in classical potential theory to extend the concept of a harmonic function, by allowing the definition of a function which is 'harmonic at infinity'...
.
Transformation on coordinates
In the following we shall use imaginary time ( ) so that space-time is Euclidean and the equations are simpler. The Poincaré transformations are given by the coordinate transformation on space-time parametrized by the 4-vectors V
) so that space-time is Euclidean and the equations are simpler. The Poincaré transformations are given by the coordinate transformation on space-time parametrized by the 4-vectors V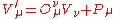
where
 is an orthogonal matrix
is an orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
and
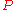 is a 4-vector. Applying this transformation twice on a 4-vector gives a third transformation of the same form. The basic invariant under this transformation is the space-time length given by the distance between two space-time points given by 4-vectors x and y:
is a 4-vector. Applying this transformation twice on a 4-vector gives a third transformation of the same form. The basic invariant under this transformation is the space-time length given by the distance between two space-time points given by 4-vectors x and y: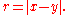
These transformations are subgroups of general 1-1 conformal transformations on space-time. It is possible to extend these transformations to include all 1-1 conformal transformations on space-time
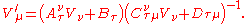
We must also have an equivalent condition to the orthogonality condition of the Poincaré transformations:
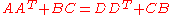
Because one can divide the top and bottom of the transformation by
 we lose no generality by setting
we lose no generality by setting  to the unit matrix. We end up with
to the unit matrix. We end up with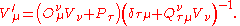
Applying this transformation twice on a 4-vector gives a transformation of the same form. The new symmetry of 'inversion' is given by the 3-tensor
 This symmetry becomes Poincaré symmetry if we set
This symmetry becomes Poincaré symmetry if we set  When
When 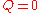 the second condition requires that
the second condition requires that  is an orthogonal matrix. This transformation is 1-1 meaning that each point is mapped to a unique point only if we theoretically include the points at infinity.
is an orthogonal matrix. This transformation is 1-1 meaning that each point is mapped to a unique point only if we theoretically include the points at infinity.Invariants
The invariants for this symmetry in 4 dimensions is unknown however it is known that the invariant requires a minimum of 4 space-time points. In one dimension, the invariant is the well known cross-ratioCross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
from Möbius transformations:
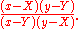
Because the only invariants under this symmetry involve a minimum of 4 points, this symmetry cannot be a symmetry of point particle theory. Point particle theory relies on knowing the lengths of paths of particles through space-time (e.g., from
 to
to 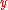 ). The symmetry can be a symmetry of a string theory
). The symmetry can be a symmetry of a string theoryString theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
in which the strings are uniquely determined by their endpoints. The propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
for this theory for a string starting at the endpoints
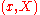 and ending at the endpoints
and ending at the endpoints 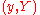 is a conformal function of the 4-dimensional invariant. A string field in endpoint-string theory is a function over the endpoints.
is a conformal function of the 4-dimensional invariant. A string field in endpoint-string theory is a function over the endpoints.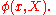
Physical evidence
Although it is natural to generalize the Poincaré transformations in order to find hidden symmetries in physics and thus narrow down the number of possible theories of high-energy physics, it is difficult to experimentally examine this symmetry as it is not possible to transform an object under this symmetry. The indirect evidence of this symmetry is given by how accurately fundamental theories of physics that are invariant under this symmetry make predictions. Other indirect evidence is whether theories that are invariant under this symmetry lead to contradictions such as giving probabilities greater than 1. So far there has been no direct evidence that the fundamental constituents of the Universe are strings. The symmetry could also be a broken symmetry meaning that although it is a symmetry of physics, the Universe has 'frozen out' in one particular direction so this symmetry is no longer evident.See also
- Rotation groupRotation groupIn mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
- Coordinate rotations and reflectionsCoordinate rotations and reflectionsIn geometry, 2D coordinate rotations and reflections are two kinds of Euclidean plane isometries which are related to one another.A rotation in the plane can be formed by composing a pair of reflections. First reflect a point P to its image P′ on the other side of line L1...
- Spacetime symmetriesSpacetime symmetriesSpacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems, spacetime symmetries finding ample application in the study of exact solutions of Einstein's field...
- CPT symmetryCPT symmetryCPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
- Field (physics)Field (physics)In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
- superstrings

