
Isoparametric manifold
Encyclopedia
In Riemannian geometry
, an isoparametric manifold is a type of (immersed) submanifold
of Euclidean space
whose normal bundle
is flat and whose principal curvatures are constant along any parallel
normal vector field. The set of isoparametric manifolds is stable under the mean curvature flow
.
Another example is as follows. Suppose that G is a Lie group
and G/H is a symmetric space
with canonical decomposition
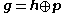
of the Lie algebra
g of G into a direct sum (orthogonal with respect to the Killing form
) of the Lie algebra h or H with a complementary subspace p. Then an orbit of the adjoint representation
of H on p is an isoparametric manifold in p.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, an isoparametric manifold is a type of (immersed) submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
whose normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
is flat and whose principal curvatures are constant along any parallel
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
normal vector field. The set of isoparametric manifolds is stable under the mean curvature flow
Mean curvature flow
In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold . Intuitively, a family of surfaces evolves under mean curvature flow if the velocity of which a point on the surface moves is given by the mean...
.
Examples
The simplest example of an isoparametric manifold is a sphere in Euclidean space.Another example is as follows. Suppose that G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and G/H is a symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
with canonical decomposition
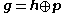
of the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
g of G into a direct sum (orthogonal with respect to the Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
) of the Lie algebra h or H with a complementary subspace p. Then an orbit of the adjoint representation
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
of H on p is an isoparametric manifold in p.

