Jacobi's elliptic functions
Encyclopedia
In mathematics
, the Jacobi elliptic functions are a set of basic elliptic function
s, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications (e.g. the equation of the pendulum
—also see pendulum (mathematics)
). They also have useful analogies to the functions of trigonometry
, as indicated by the matching notation sn for sin. The Jacobi elliptic functions occur more in practical problems than the Weierstrass elliptic functions. They were introduced by Carl Gustav Jakob Jacobi
, around 1830.
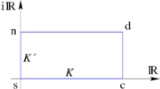
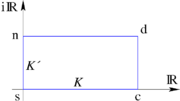 There are twelve Jacobian elliptic functions. Each of the twelve corresponds to an arrow drawn from one corner of a rectangle to another. The corners of the rectangle are labeled, by convention, s, c, d and n. The rectangle is understood to be lying on the complex plane
There are twelve Jacobian elliptic functions. Each of the twelve corresponds to an arrow drawn from one corner of a rectangle to another. The corners of the rectangle are labeled, by convention, s, c, d and n. The rectangle is understood to be lying on the complex plane
, so that s is at the origin, c is at the point K on the real axis, d is at the point K + iK' and n is at point iK' on the imaginary axis. The numbers K and K' are called the quarter periods. The twelve Jacobian elliptic functions are then pq, where each of p and q is one of the letters s, c, d, n.
The Jacobian elliptic functions are then the unique doubly periodic, meromorphic functions satisfying the following three properties:
More generally, there is no need to impose a rectangle; a parallelogram will do. However, if K and iK' are kept on the real and imaginary axis, respectively, then the Jacobi elliptic functions pq u will be real functions when u is real.
 , where
, where  . A more extensive review and definition of these alternatives, their complements, and the associated notation schemes are given in the articles on elliptic integrals and quarter period.
. A more extensive review and definition of these alternatives, their complements, and the associated notation schemes are given in the articles on elliptic integrals and quarter period.
of the first kind. This is perhaps the easiest definition to understand. Let

Then the elliptic function sn u is given by

and cn u is given by

and

Here, the angle is called the amplitude. On occasion, dn u = Δ(u) is called the delta amplitude. In the above, the value m is a free parameter, usually taken to be real, 0 ≤ m ≤ 1, and so the elliptic functions can be thought of as being given by two variables, the amplitude
is called the amplitude. On occasion, dn u = Δ(u) is called the delta amplitude. In the above, the value m is a free parameter, usually taken to be real, 0 ≤ m ≤ 1, and so the elliptic functions can be thought of as being given by two variables, the amplitude  and the parameter m.
and the parameter m.
The remaining nine elliptic functions are easily built from the above three, and are given in a section below.
Note that when , that u then equals the quarter period K.
, that u then equals the quarter period K.
 as
as  , and
, and  respectively as
respectively as  (the theta constants) then the elliptic modulus k is
(the theta constants) then the elliptic modulus k is  . If we set
. If we set  , we have
, we have



Since the Jacobi functions are defined in terms of the elliptic modulus , we need to invert this and find τ in terms of k. We start from
, we need to invert this and find τ in terms of k. We start from  , the complementary modulus. As a function of τ it is
, the complementary modulus. As a function of τ it is

Let us first define

Then define the nome q as and expand
and expand  as a power series in the nome q, we obtain
as a power series in the nome q, we obtain

Reversion of series now gives

Since we may reduce to the case where the imaginary part of τ is greater than or equal to 1/2 sqrt(3), we can assume the absolute value of q is less than or equal to exp(-1/2 sqrt(3) π) ~ 0.0658; for values this small the above series converges very rapidly and easily allows us to find the appropriate value for q.
the reciprocals of the three functions above:

Similarly, the ratios of the three primary functions correspond to the first letter of the numerator followed by the first letter of the denominator:

More compactly, we have

where each of p, q, and r is any of the letters s, c, d, n, with the understanding that ss = cc = dd = nn = 1.
(This notation is due to Gudermann and Glaisher
and is not Jacobi's original notation.)


From this we see that (cn, sn, dn) parametrizes an elliptic curve
which is the intersection of the two quadric
s defined by the above two equations. We now may define a group law for points on this curve by the addition formulas for the Jacobi functions





where and
and  .
.
Additional relations between squares can be obtained by noting that and that
and that
 where p, q, r are any of the letters s, c, d, n and ss = cc = dd = nn = 1.
where p, q, r are any of the letters s, c, d, n and ss = cc = dd = nn = 1.
 and let the argument be
and let the argument be  . Then the functions have expansions as Lambert series
. Then the functions have expansions as Lambert series



s of the three basic Jacobi elliptic functions are:



With the addition theorems above and for a given k with 0 < k < 1 they therefore are solutions to the following nonlinear ordinary differential equation
s:
is a map projection
based on Jacobian elliptic functions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Jacobi elliptic functions are a set of basic elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications (e.g. the equation of the pendulum
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
—also see pendulum (mathematics)
Pendulum (mathematics)
The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allows the equations of motion to be solved analytically for small-angle oscillations.- Simple gravity pendulum :...
). They also have useful analogies to the functions of trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, as indicated by the matching notation sn for sin. The Jacobi elliptic functions occur more in practical problems than the Weierstrass elliptic functions. They were introduced by Carl Gustav Jakob Jacobi
Carl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
, around 1830.
Introduction

Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, so that s is at the origin, c is at the point K on the real axis, d is at the point K + iK
The Jacobian elliptic functions are then the unique doubly periodic, meromorphic functions satisfying the following three properties:
- There is a simple zero at the corner p, and a simple pole at the corner q.
- The step from p to q is equal to half the period of the function pq u; that is, the function pq u is periodic in the direction pq, with the period being twice the distance from p to q. The function pq u is also periodic in the other two directions, with a period such that the distance from p to one of the other corners is a quarter period.
- If the function pq u is expanded in terms of u at one of the corners, the leading term in the expansion has a coefficient of 1. In other words, the leading term of the expansion of pq u at the corner p is u; the leading term of the expansion at the corner q is 1/u, and the leading term of an expansion at the other two corners is 1.
More generally, there is no need to impose a rectangle; a parallelogram will do. However, if K and iK' are kept on the real and imaginary axis, respectively, then the Jacobi elliptic functions pq u will be real functions when u is real.
Notation
The elliptic functions can be given in a variety of notations, which can make the subject unnecessarily confusing. Elliptic functions are functions of two variables. The first variable might be given in terms of the amplitude φ, or more commonly, in terms of u given below. The second variable might be given in terms of the parameter m, or as the elliptic modulus k, where k2 = m, or in terms of the modular angle , where
, where  . A more extensive review and definition of these alternatives, their complements, and the associated notation schemes are given in the articles on elliptic integrals and quarter period.
. A more extensive review and definition of these alternatives, their complements, and the associated notation schemes are given in the articles on elliptic integrals and quarter period.Definition as inverses of elliptic integrals
The above definition, in terms of the unique meromorphic functions satisfying certain properties, is quite abstract. There is a simpler, but completely equivalent definition, giving the elliptic functions as inverses of the incomplete elliptic integralElliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
of the first kind. This is perhaps the easiest definition to understand. Let

Then the elliptic function sn u is given by

and cn u is given by

and

Here, the angle
 is called the amplitude. On occasion, dn u = Δ(u) is called the delta amplitude. In the above, the value m is a free parameter, usually taken to be real, 0 ≤ m ≤ 1, and so the elliptic functions can be thought of as being given by two variables, the amplitude
is called the amplitude. On occasion, dn u = Δ(u) is called the delta amplitude. In the above, the value m is a free parameter, usually taken to be real, 0 ≤ m ≤ 1, and so the elliptic functions can be thought of as being given by two variables, the amplitude  and the parameter m.
and the parameter m.The remaining nine elliptic functions are easily built from the above three, and are given in a section below.
Note that when
 , that u then equals the quarter period K.
, that u then equals the quarter period K.Definition in terms of theta functions
Equivalently, Jacobi elliptic functions can be defined in terms of his theta functions. If we abbreviate as
as  , and
, and  respectively as
respectively as  (the theta constants) then the elliptic modulus k is
(the theta constants) then the elliptic modulus k is  . If we set
. If we set  , we have
, we have


Since the Jacobi functions are defined in terms of the elliptic modulus
 , we need to invert this and find τ in terms of k. We start from
, we need to invert this and find τ in terms of k. We start from  , the complementary modulus. As a function of τ it is
, the complementary modulus. As a function of τ it is
Let us first define

Then define the nome q as
 and expand
and expand  as a power series in the nome q, we obtain
as a power series in the nome q, we obtain
Reversion of series now gives

Since we may reduce to the case where the imaginary part of τ is greater than or equal to 1/2 sqrt(3), we can assume the absolute value of q is less than or equal to exp(-1/2 sqrt(3) π) ~ 0.0658; for values this small the above series converges very rapidly and easily allows us to find the appropriate value for q.
Minor functions
Reversing the order of the two letters of the function name results inthe reciprocals of the three functions above:

Similarly, the ratios of the three primary functions correspond to the first letter of the numerator followed by the first letter of the denominator:

More compactly, we have

where each of p, q, and r is any of the letters s, c, d, n, with the understanding that ss = cc = dd = nn = 1.
(This notation is due to Gudermann and Glaisher
James Whitbread Lee Glaisher
James Whitbread Lee Glaisher son of James Glaisher, the meteorologist, was a prolific English mathematician.He was educated at St Paul's School and Trinity College, Cambridge, where he was second wrangler in 1871...
and is not Jacobi's original notation.)
Addition theorems
The functions satisfy the two algebraic relations

From this we see that (cn, sn, dn) parametrizes an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
which is the intersection of the two quadric
Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
s defined by the above two equations. We now may define a group law for points on this curve by the addition formulas for the Jacobi functions

Relations between squares of the functions




where
 and
and  .
.Additional relations between squares can be obtained by noting that
 and that
and that where p, q, r are any of the letters s, c, d, n and ss = cc = dd = nn = 1.
where p, q, r are any of the letters s, c, d, n and ss = cc = dd = nn = 1.Expansion in terms of the nome
Let the nome be and let the argument be
and let the argument be  . Then the functions have expansions as Lambert series
. Then the functions have expansions as Lambert series


Jacobi elliptic functions as solutions of nonlinear ordinary differential equations
The derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of the three basic Jacobi elliptic functions are:



With the addition theorems above and for a given k with 0 < k < 1 they therefore are solutions to the following nonlinear ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s:
-
 solves the differential equations
solves the differential equations
-
-
- and
-
-
 solves the differential equations
solves the differential equations
-
-
- and
-
-
 solves the differential equations
solves the differential equations
-
-
- and
-
Map projection
The Peirce quincuncial projectionPeirce quincuncial projection
The Peirce quincuncial projection is a conformal map projection that presents the sphere as a square...
is a map projection
Map projection
A map projection is any method of representing the surface of a sphere or other three-dimensional body on a plane. Map projections are necessary for creating maps. All map projections distort the surface in some fashion...
based on Jacobian elliptic functions.
See also
- Elliptic integralElliptic integralIn integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
- Elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
- Schwarz–Christoffel mapping
- Carlson symmetric formCarlson symmetric formIn mathematics, the Carlson symmetric forms of elliptic integrals are a small canonical set of elliptic integrals to which all others may be reduced. They are a modern alternative to the Legendre forms...
- Weierstrass's elliptic functionsWeierstrass's elliptic functionsIn mathematics, Weierstrass's elliptic functions are elliptic functions that take a particularly simple form; they are named for Karl Weierstrass...
- Jacobi theta function
- Ramanujan theta functionRamanujan theta functionIn mathematics, particularly q-analog theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties. In particular, the Jacobi triple product takes on a particularly elegant form when written in terms of the Ramanujan theta...







