
Janko group J3
Encyclopedia
In mathematics
, the third Janko group J3, also known as the Higman-Janko-McKay group, is a finite
simple
sporadic group
of order 50232960. Evidence for its existence was uncovered by , and it was shown to exist by . Janko predicted both J3 and J2 as simple groups having 21+4:A5 as a centralizer of an involution.
J3 has an outer automorphism group
of order 2 and a Schur multiplier
of order 3, and its triple cover has a unitary 9 dimensional representation
over the field with 4 elements. constructed it via an underlying geometry. and it has a modular representation of dimension eighteen over the finite field of nine elements.
J3 is one of the 6 sporadic simple groups called the pariahs
, because showed that it is not found within the Monster group
.
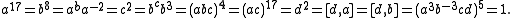
A presentation for J3 in terms of (different) generators a, b, c, d is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the third Janko group J3, also known as the Higman-Janko-McKay group, is a finite
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
sporadic group
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
of order 50232960. Evidence for its existence was uncovered by , and it was shown to exist by . Janko predicted both J3 and J2 as simple groups having 21+4:A5 as a centralizer of an involution.
J3 has an outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of order 2 and a Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
of order 3, and its triple cover has a unitary 9 dimensional representation
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
over the field with 4 elements. constructed it via an underlying geometry. and it has a modular representation of dimension eighteen over the finite field of nine elements.
J3 is one of the 6 sporadic simple groups called the pariahs
Pariah group
In mathematical group theory, the term pariah was introduced by to refer to the six sporadic simple groups that are not subquotients of the monster simple group.These groups are:*Three of the Janko groups: J1, J3, and J4.*The Lyons group...
, because showed that it is not found within the Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
.
Presentations
In terms of generators a, b, c, and d its automorphism group J3:2 can be presented as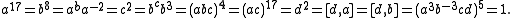
A presentation for J3 in terms of (different) generators a, b, c, d is
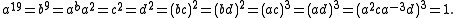
Maximal subgroups
showed that J3 has 9 conjugacy classes of maximal subgroups:- PSL(2,16):2, order 8160
- PSL(2,19), order 3420
- PSL(2,19), conjugate to preceding class in J3:2
- 24:(3 × A5), order 2880
- PSL(2,17), order 2448
- (3 × A6):22, order 2160 - normalizer of subgroup of order 3
- 32+1+2:8, order 1944 - normalizer of Sylow 3-subgroup
- 21+4:A5, order 1920 - centralizer of involution
- 22+4:(3 × S3), order 1152
External links
- Atlas of Finite Group Representations: J3 version 2
- Atlas of Finite Group Representations: J3 version 3

