Sporadic group
Encyclopedia
In the mathematical field of group theory
, a sporadic group is one of the 26 exceptional groups
in the classification of finite simple groups
. A simple group
is a group G that does not have any normal subgroup
s except for the subgroup consisting only of the identity element, and G itself. The classification theorem states that the list of finite simple groups consists of 18 countably infinite families, plus 26 exceptions that do not follow such a systematic pattern. These are the sporadic groups. They are also known as the sporadic simple groups, or the sporadic finite groups. Sometimes (such as by John Conway
) the Tits group
is regarded as a sporadic group (because it is not strictly a group of Lie type
), in which case there are 27 sporadic groups.
The Monster group
is the largest of the sporadic groups and contains all but six of the other sporadic groups as subgroup
s or subquotient
s.
in the 1860s and the other 21 were found between 1965 and 1975. Several of these groups were predicted to exist before they were constructed. Most of the groups are named after the mathematician(s) who first predicted their existence. The full list is:
Matrix representations
over finite fields for all the sporadic groups have been constructed.
The earliest use of the term "sporadic group" may be where he comments about the Mathieu groups: "These apparently sporadic simple groups would probably repay a closer examination than they have yet received".
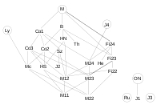
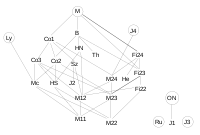
Diagram is based on diagram given in . The sporadic groups also have a lot of subgroups which are not sporadic but these are not shown on the diagram because they are too numerous.
as subgroup
s or quotients
of subgroups. The six exceptions are J1, J3, J4, O'N, Ru and Ly. These six groups are sometimes known as the pariahs
.
The remaining twenty groups have been called the Happy Family by Robert Griess, and can be organized into three generations.
s on n points. They are all subgroups of M24, which is a permutation group on 24
points.
s of the automorphism group of a lattice in 24
dimensions called the Leech lattice
:
(This series continues further: the product of M12 and a group of order 11 is the centralizer of an element of order 11 in M.)
The Tits group
also belongs in this generation: there is a subgroup S4 ×2F4(2)′ normalising a 2C2 subgroup of B, giving rise to a subgroup
2·S4 ×2F4(2)′ normalising a certain Q8 subgroup of the Monster.
2F4(2)′ is also a subgroup of the Fischer groups Fi22, Fi23 and Fi24′, and of the Baby Monster B.
2F4(2)′ is also a subgroup of the (pariah) Rudvalis group Ru, and has
no involvements in sporadic simple groups except the containments we have already mentioned.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a sporadic group is one of the 26 exceptional groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
in the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
. A simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
is a group G that does not have any normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s except for the subgroup consisting only of the identity element, and G itself. The classification theorem states that the list of finite simple groups consists of 18 countably infinite families, plus 26 exceptions that do not follow such a systematic pattern. These are the sporadic groups. They are also known as the sporadic simple groups, or the sporadic finite groups. Sometimes (such as by John Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
) the Tits group
Tits group
In mathematics, the Tits group 2F4′ is a finite simple group of order 17971200 = 211 · 33 · 52 · 13 found by ....
is regarded as a sporadic group (because it is not strictly a group of Lie type
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
), in which case there are 27 sporadic groups.
The Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
is the largest of the sporadic groups and contains all but six of the other sporadic groups as subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s or subquotient
Subquotient
In the mathematical fields of category theory and abstract algebra, a subquotient is a quotient object of a subobject. Subquotients are particularly important in group theory, where they are also known as sections, and in abelian categories....
s.
Names of the sporadic groups
Five of the sporadic groups were discovered by MathieuÉmile Léonard Mathieu
Émile Léonard Mathieu was a French mathematician. He is most famous for his work in group theory and mathematical physics. He has given his name to the Mathieu functions, Mathieu groups and Mathieu transformation...
in the 1860s and the other 21 were found between 1965 and 1975. Several of these groups were predicted to exist before they were constructed. Most of the groups are named after the mathematician(s) who first predicted their existence. The full list is:

- Mathieu groupMathieu groupIn the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
s M11, M12, M22, M23, M24 - Janko groupJanko groupIn mathematics, a Janko group is one of the four sporadic simple groups named for Zvonimir Janko. Janko constructed the first Janko group J1 in 1965. At the same time, Janko also predicted the existence of J2 and J3. In 1976, he suggested the existence of J4...
s J1, J2 or HJ, J3 or HJM, J4 - Conway groupConway groupIn mathematics, the Conway groups Co1, Co2, and Co3 are three sporadic groups discovered by John Horton Conway.The largest of the Conway groups, Co1, of order...
s Co1 or F2−, Co2, Co3 - Fischer groupFischer groupIn mathematics, the Fischer groups are the three sporadic simple groups Fi22, Fi23,Fi24' introduced by .- 3-transposition groups :...
s Fi22, Fi23, Fi24′ or F3+ - Higman–Sims group HS
- McLaughlin groupMcLaughlin group (mathematics)In the mathematical discipline known as group theory, the McLaughlin group McL is a sporadic simple group of order 27 · 36 · 53· 7 · 11 = 898,128,000, discovered by as an index 2 subgroup of a rank 3 permutation group acting on the McLaughlin graph with 275 =1+112+162 vertices...
McL - Held groupHeld groupIn the mathematical field of group theory, the Held group He is one of the 26 sporadic simple groups, and has order...
He or F7+ or F7 - Rudvalis groupRudvalis groupIn the mathematical field of group theory, the Rudvalis group Ru is a sporadic simple group of order-Properties:The Rudvalis group acts as a rank 3 permutation group on 4060 points, with one point stabilizer the Ree group...
Ru - Suzuki sporadic groupSuzuki sporadic groupIn mathematical group theory, the Suzuki group Suz or Sz is a sporadic simple group of order 213 · 37 · 52· 7 · 11 · 13 = 448345497600 discovered by . It is not related to the Suzuki groups of Lie type....
Suz or F3− - O'Nan groupO'Nan groupIn the mathematical field of group theory, the O'Nan group O'N is a sporadic simple group of orderThe Schur multiplier has order 3, and its outer automorphism group has order 2...
O'N - Harada–Norton group HN or F5+ or F5
- Lyons groupLyons groupIn the mathematical field of group theory, the Lyons group Ly , is a sporadic simple group of order...
Ly - Tits groupTits groupIn mathematics, the Tits group 2F4′ is a finite simple group of order 17971200 = 211 · 33 · 52 · 13 found by ....
T - Thompson groupThompson group (finite)In the mathematical field of group theory, the Thompson group Th, found by and constructed by , is a sporadic simple group of orderThe centralizer of an element of order 3 of type 3C in the Monster group is a product of the Thompson group and a group of order 3, as a result of which the Thompson...
Th or F3|3 or F3 - Baby Monster groupBaby Monster groupIn the mathematical field of group theory, the Baby Monster group B is a group of orderThe Baby Monster group is one of the sporadic groups, and has the second highest order of these, with the highest order being that of the Monster group...
B or F2+ or F2 - Fischer–Griess Monster groupMonster groupIn the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
M or F1
Matrix representations
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
over finite fields for all the sporadic groups have been constructed.
The earliest use of the term "sporadic group" may be where he comments about the Mathieu groups: "These apparently sporadic simple groups would probably repay a closer examination than they have yet received".
Diagram is based on diagram given in . The sporadic groups also have a lot of subgroups which are not sporadic but these are not shown on the diagram because they are too numerous.
Organization
Of the 26 sporadic groups, 20 can be seen inside the Monster groupMonster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
as subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s or quotients
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of subgroups. The six exceptions are J1, J3, J4, O'N, Ru and Ly. These six groups are sometimes known as the pariahs
Pariah group
In mathematical group theory, the term pariah was introduced by to refer to the six sporadic simple groups that are not subquotients of the monster simple group.These groups are:*Three of the Janko groups: J1, J3, and J4.*The Lyons group...
.
The remaining twenty groups have been called the Happy Family by Robert Griess, and can be organized into three generations.
First generation: the Mathieu groups
The Mathieu groups Mn (for n = 11, 12, 22, 23 and 24) are multiply transitive permutation groupPermutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s on n points. They are all subgroups of M24, which is a permutation group on 24
24 (number)
24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...
points.
Second generation: the Leech lattice
The second generation are all subquotientSubquotient
In the mathematical fields of category theory and abstract algebra, a subquotient is a quotient object of a subobject. Subquotients are particularly important in group theory, where they are also known as sections, and in abelian categories....
s of the automorphism group of a lattice in 24
24 (number)
24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...
dimensions called the Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
:
- Co1 is the quotient of the automorphism group by its center {±1}
- Co2 is the stabilizer of a type 2 (i.e., length 2) vector
- Co3 is the stabilizer of a type 3 (i.e., length √6) vector
- Suz is the group of automorphisms preserving a complex structure (modulo its center)
- McL is the stabilizer of a type 2-2-3 triangle
- HS is the stabilizer of a type 2-3-3 triangle
- J2 is the group of automorphisms preserving a quaternionic structure (modulo its center).
Third generation: other subgroups of the Monster
The third generation consists of subgroups which are closely related to the Monster group M:- B or F2 has a double cover which is the centralizer of an element of order 2 in M
- Fi24′ has a triple cover which is the centralizer of an element of order 3 in M (in conjugacy classConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
"3A") - Fi23 is a subgroup of Fi24′
- Fi22 has a double cover which is a subgroup of Fi23
- The product of Th = F3 and a group of order 3 is the centralizer of an element of order 3 in M (in conjugacy class "3C")
- The product of HN = F5 and a group of order 5 is the centralizer of an element of order 5 in M
- The product of He = F7 and a group of order 7 is the centralizer of an element of order 7 in M.
- Finally, the Monster group itself is considered to be in this generation.
(This series continues further: the product of M12 and a group of order 11 is the centralizer of an element of order 11 in M.)
The Tits group
Tits group
In mathematics, the Tits group 2F4′ is a finite simple group of order 17971200 = 211 · 33 · 52 · 13 found by ....
also belongs in this generation: there is a subgroup S4 ×2F4(2)′ normalising a 2C2 subgroup of B, giving rise to a subgroup
2·S4 ×2F4(2)′ normalising a certain Q8 subgroup of the Monster.
2F4(2)′ is also a subgroup of the Fischer groups Fi22, Fi23 and Fi24′, and of the Baby Monster B.
2F4(2)′ is also a subgroup of the (pariah) Rudvalis group Ru, and has
no involvements in sporadic simple groups except the containments we have already mentioned.
Table of the sporadic group orders
| Group | Order | 1SF Significant figures The significant figures of a number are those digits that carry meaning contributing to its precision. This includes all digits except:... | Factorized order |
|---|---|---|---|
| F1 or M | 808017424794512875886459904961710757005754368000000000 | ≈ 8 | 246 · 320 · 59 · 76 · 112 · 133 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71 |
| F2 or B | 4154781481226426191177580544000000 | ≈ 4 | 241 · 313 · 56 · 72 · 11 · 13 · 17 · 19 · 23 · 31 · 47 |
| Fi24' or F3+ | 1255205709190661721292800 | ≈ 1 | 221 · 316 · 52 · 73 · 11 · 13 · 17 · 23 · 29 |
| Fi23 | 4089470473293004800 | ≈ 4 | 218 · 313 · 52 · 7 · 11 · 13 · 17 · 23 |
| Fi22 | 64561751654400 | ≈ 6 | 217 · 39 · 52 · 7 · 11 · 13 |
| F3 or Th | 90745943887872000 | ≈ 9 | 215 · 310 · 53 · 72 · 13 · 19 · 31 |
| Ly | 51765179004000000 | ≈ 5 | 28 · 37 · 56 · 7 · 11 · 31 · 37 · 67 |
| F5 or HN | 273030912000000 | ≈ 3 | 214 · 36 · 56 · 7 · 11 · 19 |
| Co1 | 4157776806543360000 | ≈ 4 | 221 · 39 · 54 · 72 · 11 · 13 · 23 |
| Co2 | 42305421312000 | ≈ 4 | 218 · 36 · 53 · 7 · 11 · 23 |
| Co3 | 495766656000 | ≈ 5 | 210 · 37 · 53 · 7 · 11 · 23 |
| O'N | 460815505920 | ≈ 5 | 29 · 34 · 5 · 73 · 11 · 19 · 31 |
| Suz | 448345497600 | ≈ 4 | 213 · 37 · 52 · 7 · 11 · 13 |
| Ru | 145926144000 | ≈ 1 | 214 · 33 · 53 · 7 · 13 · 29 |
| He | 4030387200 | ≈ 4 | 210 · 33 · 52 · 73 · 17 |
| McL | 898128000 | ≈ 9 | 27 · 36 · 53 · 7 · 11 |
| HS | 44352000 | ≈ 4 | 29 · 32 · 53 · 7 · 11 |
| J4 | 86775571046077562880 | ≈ 9 | 221 · 33 · 5 · 7 · 113 · 23 · 29 · 31 · 37 · 43 |
| J3 or HJM | 50232960 | ≈ 5 | 27 · 35 · 5 · 17 · 19 |
| J2 or HJ | 604800 | ≈ 6 | 27 · 33 · 52 · 7 |
| J1 | 175560 | ≈ 2 | 23 · 3 · 5 · 7 · 11 · 19 |
| M24 | 244823040 | ≈ 2 | 210 · 33 · 5 · 7 · 11 · 23 |
| M23 | 10200960 | ≈ 1 | 27 · 32 · 5 · 7 · 11 · 23 |
| M22 | 443520 | ≈ 4 | 27 · 32 · 5 · 7 · 11 |
| M12 | 95040 | ≈ 1 | 26 · 33 · 5 · 11 |
| M11 | 7920 | ≈ 8 | 24 · 32 · 5 · 11 |

