
Rudvalis group
Encyclopedia
In the mathematical field of group theory
, the Rudvalis group Ru (found by and constructed by ) is a sporadic
simple group
of order
Ru is one of the six sporadic simple groups called the pariahs
, because they are not found within the Monster group
.
2F4(2), the automorphism group of the Tits group
. This representation implies a strongly regular graph
in which each vertex has 2304 neighbors and 1755 non-neighbors. Two adjacent vertices have 1328 common neighbors; two non-adjacent ones have 1208
Its Schur multiplier
has order 2, and its outer automorphism group
is trivial.
Its double cover acts on a 28-dimensional lattice over the Gaussian integer
s. Reducing this lattice modulo the principal ideal
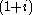
gives an action of the Rudvalis group on a 28-dimensional vector space over the field with 2 elements. Duncan (2006) used this to construct a vertex operator algebra
acted on by the double cover.
characterized the Rudvalis group by the centralizer of a central involution. gave another characterization as part of their identification of the Rudvalis group as one of the quasithin group
s.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Rudvalis group Ru (found by and constructed by ) is a sporadic
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
- 214 · 33 · 53 · 7 · 13 · 29
- = 145926144000
- ≈ 1011.
Ru is one of the six sporadic simple groups called the pariahs
Pariah group
In mathematical group theory, the term pariah was introduced by to refer to the six sporadic simple groups that are not subquotients of the monster simple group.These groups are:*Three of the Janko groups: J1, J3, and J4.*The Lyons group...
, because they are not found within the Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
.
Properties
The Rudvalis group acts as a rank 3 permutation group on 4060 points, with one point stabilizer the Ree group2F4(2), the automorphism group of the Tits group
Tits group
In mathematics, the Tits group 2F4′ is a finite simple group of order 17971200 = 211 · 33 · 52 · 13 found by ....
. This representation implies a strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
in which each vertex has 2304 neighbors and 1755 non-neighbors. Two adjacent vertices have 1328 common neighbors; two non-adjacent ones have 1208
Its Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
has order 2, and its outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
is trivial.
Its double cover acts on a 28-dimensional lattice over the Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s. Reducing this lattice modulo the principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
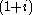
gives an action of the Rudvalis group on a 28-dimensional vector space over the field with 2 elements. Duncan (2006) used this to construct a vertex operator algebra
Vertex operator algebra
In mathematics, a vertex operator algebra is an algebraic structure that plays an important role in conformal field theory and related areas of physics...
acted on by the double cover.
characterized the Rudvalis group by the centralizer of a central involution. gave another characterization as part of their identification of the Rudvalis group as one of the quasithin group
Quasithin group
In mathematics, a quasithin group is roughly a finite simple group of characteristic 2 type and width 2. Here characteristic 2 type means that its centralizers of involutions resemble those of groups of Lie type over fields of characteristic 2, and the width is roughly the maximal rank of an...
s.

