
Jantzen filtration
Encyclopedia
In algebra, a Jantzen filtration is a filtration of a Verma module
of a semisimple Lie algebra, or a Weyl module
of a reductive algebraic group of positive characteristic. Jantzen filtrations were introduced by .
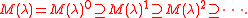
It has the following properties:
Verma module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
of a semisimple Lie algebra, or a Weyl module
Weyl module
In algebra, a Weyl module is a representation of a reductive algebraic group, introduced by and named after Hermann Weyl. In characteristic 0 these representations are irreducible, but in positive characteristic they can be reducible, and their decomposition into irreducible components can be...
of a reductive algebraic group of positive characteristic. Jantzen filtrations were introduced by .
Jantzen filtration for Verma modules
If M(λ) is a Verma module of a semisimple Lie algebra with highest weight λ, then the Janzen filtration is a decreasing filtration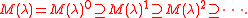
It has the following properties:
- M(λ)1 is the maximal proper submodule of M(λ)
- The quotients M(λ)k/M(λ)k+1 have non-degenerate contravariant bilinear forms.
-

- (the Jantzen sum formula)

