
Jay Hambidge
Encyclopedia

Canada
Canada is a North American country consisting of ten provinces and three territories. Located in the northern part of the continent, it extends from the Atlantic Ocean in the east to the Pacific Ocean in the west, and northward into the Arctic Ocean...
. He was a pupil at the Art Students' League
Art Students League of New York
The Art Students League of New York is an art school located on West 57th Street in New York City. The League has historically been known for its broad appeal to both amateurs and professional artists, and has maintained for over 130 years a tradition of offering reasonably priced classes on a...
in New York
New York City
New York is the most populous city in the United States and the center of the New York Metropolitan Area, one of the most populous metropolitan areas in the world. New York exerts a significant impact upon global commerce, finance, media, art, fashion, research, technology, education, and...
and of William Chase
William Merritt Chase
William Merritt Chase was an American painter known as an exponent of Impressionism and as a teacher. He is also responsible for establishing the Chase School, which later would become Parsons The New School for Design.- Early life and training :He was born in Williamsburg , Indiana, to the family...
, and a thorough student of classical art. He conceived the idea that the study of arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
with the aid of geometrical
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
designs was the foundation of the proportion and symmetry in Greek architecture, sculpture, and ceramics. Careful examination and measurements of classical buildings in Greece
Greece
Greece , officially the Hellenic Republic , and historically Hellas or the Republic of Greece in English, is a country in southeastern Europe....
, among them the Parthenon
Parthenon
The Parthenon is a temple on the Athenian Acropolis, Greece, dedicated to the Greek goddess Athena, whom the people of Athens considered their virgin patron. Its construction began in 447 BC when the Athenian Empire was at the height of its power. It was completed in 438 BC, although...
, the temple of Apollo at Bassæ
Bassae
Bassae or Bassai, Vassai or Vasses , meaning "little vale in the rocks", is an archaeological site in the northeastern part of Messinia Prefecture that was a part of Arcadia in ancient times. Bassae lies near the village of Skliros, northeast of Figaleia, south of Andritsaina and west of Megalopolis...
, of Zeus
Statue of Zeus at Olympia
The Statue of Zeus at Olympia was made by the Greek sculptor Phidias, circa 432 BC on the site where it was erected in the Temple of Zeus, Olympia, Greece. It was one of the Seven Wonders of the Ancient World.-Description:...
at Olympia
Olympia, Greece
Olympia , a sanctuary of ancient Greece in Elis, is known for having been the site of the Olympic Games in classical times, comparable in importance to the Pythian Games held in Delphi. Both games were held every Olympiad , the Olympic Games dating back possibly further than 776 BC...
and Athenæ
Athena
In Greek mythology, Athena, Athenê, or Athene , also referred to as Pallas Athena/Athene , is the goddess of wisdom, courage, inspiration, civilization, warfare, strength, strategy, the arts, crafts, justice, and skill. Minerva, Athena's Roman incarnation, embodies similar attributes. Athena is...
at Ægina
Aegina
Aegina is one of the Saronic Islands of Greece in the Saronic Gulf, from Athens. Tradition derives the name from Aegina, the mother of Aeacus, who was born in and ruled the island. During ancient times, Aegina was a rival to Athens, the great sea power of the era.-Municipality:The municipality...
, prompted him to formulate the theory of "dynamic symmetry" as demonstrated in his works Dynamic Symmetry: The Greek Vase (1920) and The Elements of Dynamic Symmetry (1926). It created a great deal of discussion, an English
English people
The English are a nation and ethnic group native to England, who speak English. The English identity is of early mediaeval origin, when they were known in Old English as the Anglecynn. England is now a country of the United Kingdom, and the majority of English people in England are British Citizens...
critic saying that Hambidge did not try to formulate a new theory, but to recover a lost technique. He found a disciple
Follower
Follower is a poem by Seamus Heaney released in his 1966 collection Death of a Naturalist. The poem is about how he admired and followed his father....
in Dr. Lacey D. Caskey, the author of Geometry of Greek Vases (1922).
Dynamic symmetry
Dynamic symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
is a proportioning system and natural design methodology described in Hambidge's books. The system uses dynamic rectangle
Dynamic rectangle
A dynamic rectangle is a right-angled, four-sided figure with dynamic symmetry, which in this case, means that aspect ratio is a distinguished value in dynamic symmetry, a proportioning system and natural design methodology described in Jay Hambidge's books...
s, including root rectangles based on ratios such as √2, √3, √5, the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
(φ = 1.618...), its square root (√φ = 1.272...), and its square (φ2 = 2.618....), and the
silver ratio
Silver ratio
In mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,...
(
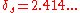 ).
).From the study of phyllotaxis
Phyllotaxis
In botany, phyllotaxis or phyllotaxy is the arrangement of leaves on a plant stem .- Pattern structure :...
and the related Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...), Hambidge says that "a much closer representation would be obtained by a substitute series such as 118, 191, 309, 500, 809, 1309, 2118, 3427, 5545, 8972, 14517, etc. One term of this series divided into the other equals 1.6180, which is the ratio needed to explain the plant design system." This substitute sequence is a generalization of the Fibonacci sequence
Generalizations of Fibonacci numbers
In mathematics, the Fibonacci numbers form a sequence defined recursively by:The Fibonacci sequence has been studied extensively and generalized in many ways, for example, by starting with other numbers than 0 and 1, by adding more than two numbers to generate the next number, or by adding objects...
that chooses 118 and 191 as the beginning numbers to generate the rest. In fact, the standard Fibonacci sequence provides the best possible rational approximations to the golden ratio for numbers of a given size.

